এমিল জুলিয়াস গাম্বেল

গাম্বেলের এক বন্ধুও একদিন খুন হয়ে গেলেন প্রকাশ্যে। গাম্বেল দেখলেন আদালতে বিচারের নামে নেহাত-ই প্রহসন হলো শুধু, বিচারক কোনো প্রমাণ-ই গ্রাহ্য করলেন না, আর উল্লাসে মেতে উঠলো নাৎসী গুণ্ডার দল। গাম্বেল বুঝতে পারলেন জার্মানির বিচারব্যবস্থাও পুরোপুরি নাৎসিবাহিনীর দখলে, আর বিচারকদের সবাই হয় নিজেই নাৎসী-সমর্থক, না হলেও নিজেকে বিকিয়ে দিয়েছেন সেই নিষ্পেষণ যন্ত্রের কাছে। (এ অব্দি পড়ে চেনা ঠেকছে, পাঠক?)

যা হোক, গাম্বেল ভয় পেলেন না। সেই ১৯২২ সালেই একটি বই ছাপিয়ে ফেললেন সাহস করে, নাম Vier Jahre politischer Mord (Four Years of Political Murder)। ১৯১৮-র নভেম্বর ৯, অর্থাৎ জার্মান রেভোলিউশনের শুরুর দিন থেকে দক্ষিণপন্থী এবং বামপন্থী রাজনৈতিক হত্যার দলিল। এইখানে গাম্বেলের সেই রাজনৈতিক হত্যার দলিল থেকে কিছুটা উদ্ধৃত করলে আশা করি খুব অন্যায় হবে না।

1. “Correspondingly, the right is inclined to hope that it could annihilate the left opposition, which is carried by hopes for a radically different economic order, by defeating its leaders.  And the right has done it: all of the leaders of the left who openly opposed the war and whom the workers trusted–Liebknecht, Luxemburg, Eisner, [Gustav] Landauer, [Leo] Jogisches, et al–are dead.
2. The effectiveness of this technique is for the moment indisputable.  The left no longer has any significant leaders, no more people toward whom the masses have the feeling: he has suffered so much for us, dared so much for us that we can trust him blindly.  The working-class movement has thereby doubtlessly been set back by years.  This success is all the greater since in no case has punishment occurred.
3. The unbelievable leniency of the court is also quite well known to the perpetrators. . . . Today the [right wing] perpetrator risks nothing at all.  Powerful organizations with an extensive network of confidantes over the whole country provide him with shelter, protection, and material sustenance.  “Right-minded” bureaucrats and police chiefs supply falsified papers for potentially necessary trips abroad. . . .  The beneficiaries live magnificently and happily in the best hotels.”

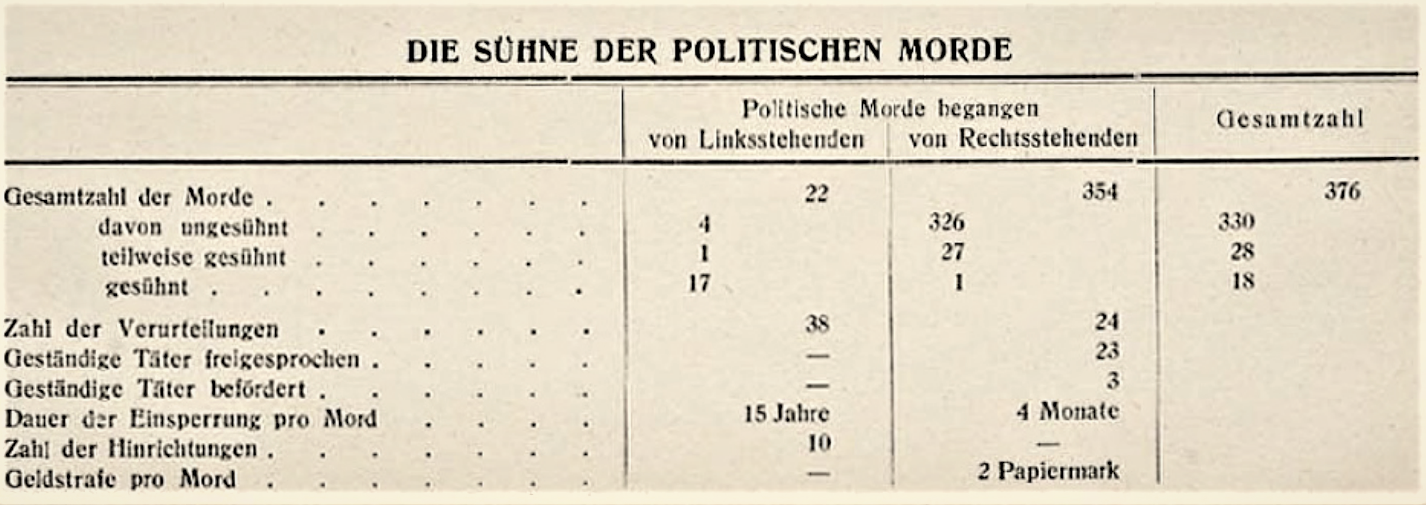
গাম্বেলের ১৯২২ সালের বই থেকে মূল টেবল (উপরে যার থেকে একটি অংশ দেওয়া হলো)

১৯৩৩-এ নাৎসি বাহিনী ক্ষমতায় আসে যখন, গাম্বেল তখন সুইজারল্যাণ্ডে গেছেন সেমিনারে। খবর পেয়ে তক্ষুণি দেশে ফিরে ঝাঁপিয়ে পড়তে চেয়েছিলেন বিরুদ্ধ-সংগ্রামে, বন্ধুরা বোঝান যে গাম্বেল বর্ডার পেরোনোর আগেই গ্রেফতার হবেন, খুন-ও।

সেই সময়েই আরও কিছু ইহুদি অধ্যাপক, যেমন বিখ্যাত প্রোবাবিলিস্ট রিচার্ড ভন মিসেস, আগে থেকেই পরিস্থিতি বুঝতে পেরে পালিয়ে যান ফ্রান্সে। গাম্বেল-ও পৌঁছন দক্ষিণ ফ্রান্সে, কিন্তু বেশীদিন নিরাপদ রইলেন না কেউ-ই, ’৪০-এই ফ্রান্সে নাৎসীবাদের থাবা এসে পৌঁছলো। গাম্বেল ও আরও বেশ কিছু মানুষ তখন ‘এনিমি অফ দ্য স্টেট’ – নাৎসিবাহিনী চায় ফ্রান্সের নাম-কা-ওয়াস্তে সরকার হস্তারন্তিত করুক তাদের। হয়তো তাই-ই হতো, রক্ষাকর্তার ভূমিকায় নামলেন মার্সেই-এর তৎকালীন আমেরিকান কনসাল হিরাম বিংগহ্যাম ফোর, স্টেট ডিপার্টমেন্টের নির্দেশিকা অমান্য করে ভিসা দিয়ে যুক্তরাষ্ট্রে পাঠিয়ে দিলেন গাম্বেল ও অন্যান্য জার্মান উদবাস্তুদের। বিংগহ্যাম চাকরিটি অবশ্য অচিরেই খোয়ালেন, কিন্তু সাক্ষাৎ মৃত্যুর শমন থেকে বাঁচিয়ে দিলেন অনেকগুলি মানুষের। অন্ধকারের মাঝে এও এক আলো। গাম্বেল এসে যোগ দিলেন কলম্বিয়া বিশ্ববিদ্যালয়ে, যেখান থেকেই কিছু বছর পরে প্রকাশিত হবে সেই এক্সট্রিম থিওরির বাইবেলটি।

গল্পের সুতো হাত থেকে পড়ে গেলে কোথা থেকে কোথায় টেনে নিয়ে যায় সে বোঝা দায়, এই যেমন এখন এক্সট্রিম ভ্যালুর গল্প বলতে বলতে চলে এসেছি এক্সট্রিমিস্টদের ভয়ের গল্পে। গল্পের অবশ্য আর বেশী বাকি নেই, নাৎসী বাহিনীর কী হয়েছে সে ইতিহাস জানে, কিন্তু সেই যে ফকনার বলেছিলেন না, ‘the past is never dead, it is not even the past’ … দক্ষিণপন্থী ব্রাউন-শার্ট আর নেই, কিন্তু নাৎসীবাদ যে পৃথিবী থেকে সম্পূর্ণ উড়ে গেছে এ কথা অমূলক। এই প্রতিবেদন লেখার সময়েই জানি শুধু টুইটারে কী ভয়ঙ্কর অ্যান্টি-সেমিটিক ঘৃণার মেসেজ আর হুমকি চলছে প্রতিনিয়ত – সে নিকষ অন্ধকারের কোনো শেষ নেই।

বা হয়তো আছে, আমাদের অন্তিম মূল্য হয়তো ঘৃণায় নয়, সত্যিই প্রেমে, তবে কোনো এক্সট্রিম ভ্যালুর থিওরির সাধ্য নেই সেই সম্ভাবনার ঠিকঠাক প্রেডিকশন করা। আর কী জানেন তো, গভীর-গভীরতম অসুখ তো আসলে পৃথিবীর নয়, মানুষের। গাম্বেলের সেই রাজনৈতিক হত্যার দলিল থেকে আরেকটি মর্মান্তিক উক্তি দিয়ে শেষ করবঃ

“Public opinion in general approves of this procedure.  For clever propaganda has taught it that every enemy of militarism is a Spartacist, therefore an enemy of humanity, therefore open game.”

তবে তাও আশা রাখি, সেই মূঢ় ম্লান স্রোতের মধ্যে থেকেও একজন গাম্বেল উঠে আসবেন প্রত্যেকবার, আর রাজনৈতিক হত্যার রেখে যাওয়া দলিল আমাদের বলে দেবে আসলে ইতিহাস থেকে কিছুই কোনওদিন-ই শিখে উঠতে পারব না আমরা।

পুনশ্চ

1. রিচার্ড ভন মিসেস আরেক জন বিরল প্রতিভা, যিনি এক-ই সাথে অঙ্ক, স্ট্যাটিসটিক্স, প্রোবাবিলিটি, সলিড মেকানিক্স, ফ্লুইড মেকানিক্স, এরোনটিক্স, এরোডায়নামিক্স - সবেতেই কোনো না কোনো অবদান রেখে গেছেন। প্রথম বিশ্বযুদ্ধে অস্ট্রো-হাংগেরিয়ান আর্মিতে যোগ দেন, এবং সেই সাম্রাজ্যের (মনার্কি-র) প্রথম বড় উড়োজাহাজ বানানোর মূল কারিগর। যুদ্ধের পরে ১৩ বছর বার্লিনে থাকার সময় প্রোবাবিলিটি এবং দর্শনশাস্ত্রে উৎসাহী ভন মিসেস যে বইটি লেখেন "Wahrscheinlichkeit, Statistik und Wahrheit", সেইটিই আমাদের লাইনে তার জনপ্রিয়তম কাজ। একটি জর্নল-ও শুরু করেন এই সময়েই, ফলিত গণিত ও বলবিদ্যার। ১৯৩৩ সালে হিটলারের ক্ষমতায় আসার পরে ভন মিসেস প্রথমে যান ইস্তানবুল, লিখতে শুরু করেন ফ্রেঞ্চে, তারপর ১৯৩৯ সালে হার্ভার্ড, যার পর থেকে সব লেখাই প্রায় ইংরেজিতে। বার্লিনের ১৩ বছর থাকার সময় ভন মিসেস মন দিয়ে কবি রাইনের মারিয়া রিলকের সমস্ত কাজ সংগ্রহ করতে শুরু করেন। দেশ ছেড়ে আসার আগে তিনিই ছিলেন রিলকের বৃহত্তম ব্যক্তিগত কালেকটর, এবং বলাই বাহুল্য, একজন অথরিটি-বিশেষ।


2. অঙ্কের জগতে বার্নৌলি পরিবারের নাম সবাই জানে, এবং বোধহয় এমন কোনো শাখাই নেই যেখানে তারা কিছু না কিছু ছাপ রেখে গেছেন, এক্সট্রিম ভ্যালু থিওরি-ও তার ব্যতিক্রম নয়। ১৭০৯ সালে নিকোলাস বার্নৌলি একটি অ্যাকচুয়ারিয়াল অঙ্ক সমাধান করেছিলেন - সেইটি এইরকমঃ "ধরা যাক, 'এন' সংখ্যক সমবয়স্ক মানুষ ঠিক 'টি' সময়ের মধ্যে মারা যাবেন। তাহলে যিনি সবার শেষে মারা যাবেন, অর্থাৎ, লাস্ট সারভাইভর, তাঁর গড় বয়স কতো হওয়া উচিত? বার্নৌলির সমাধানটি খুব সুন্দর - ধরে নেওয়া যাক, 'টি' দৈর্ঘ্যের একটি সরলরেখার উপর 'এন' খানা র‍্যান্ডম বিন্দু বসানো, তাহলে কষে বের করতে হবে মূলবিন্দু (অরিজিন) থেকে দীর্ঘতম দূরত্বের গড় কত?

সূত্রনির্দেশ:

1. Salsburg, D. (2001). The lady tasting tea: How statistics revolutionized science in the twentieth century. Macmillan
2. Gumbel, E. J. (1958). Statistics of extremes. Courier Corporation.
3. Gumbel, E.J.: Vier Jahre Politischer Mord. Berlin–Fichtenau: Verlag der Neuen Gesellschaft, Berlin (1922)
4. Mathematician and chronicler of political murders, New facts on extreme value theoretician Emil J. Gumbel (https://www.sciencedaily.com/releases/2017/09/170919105203.htm)
5. Einmahl, J. J., Einmahl, J. H., & de Haan, L. (2019). Limits to human life span through extreme value theory. Journal of the American Statistical Association, 114(527), 1075-1080
6. Einmahl, J. H., & Magnus, J. R. (2008). Records in athletics through extreme-value theory. Journal of the American Statistical Association, 103(484), 1382-1391.
7. Auerbach, J., & Wan, P. (2020). Forecasting the urban skyline with extreme value theory. International Journal of Forecasting, 36(3), 814-828.