- বুলবুলভাজা আলোচনা স্বাস্থ্য শনিবারবেলা

-
ব্লাড টেস্ট, প্রসিকিউটর’স ফ্যালাসি ও ওয়ান্ডার উওম্যানের ল্যাসো – এজলাসে Bayes-বাবু
যদুবাবু
আলোচনা | স্বাস্থ্য | ০৮ মে ২০২১ | ৫২৫১ বার পঠিত | রেটিং ৫ (২ জন) - প্রথম কিস্তি | দ্বিতীয় কিস্তি | তৃতীয় কিস্তি | চতুর্থ কিস্তি | পঞ্চম কিস্তি | ষষ্ঠ কিস্তি | সপ্তম কিস্তি | অষ্টম কিস্তি | সমষ্টি থেকে ব্যষ্টি | ভক্স পপুলি | দুই লেজান্ড্রর গল্প | বিষের ইতিহাস, ইতিহাসের বিষ
আবার শুরু করবো একটা আপাত নিরীহ অঙ্ক দিয়ে।
ধরা যাক আপনি একটা ব্লাড টেস্ট করেছেন, এবং পজিটিভ রেজাল্ট পেয়েছেন। আর ডাক্তারবাবু/সরকার বলে দিয়েছেন যে এই টেস্টের ফলস পজিটিভ রেট খুব-ই কম, মাত্র ১০০০ এ ১ জন, অর্থাৎ ০.১%। তাহলেই কি ধরে নেবেন যে ওই অসুখটা সত্যি সত্যি থাকার সম্ভাবনা ৯৯.৯%?
উত্তর-টা এই যে, শুধু এইটুকু তথ্য দিয়ে বলা সম্ভব নয়। আর তার পিছনে আছে সেই অষ্টাদশ শতকের ছোট্ট একটা উপপাদ্য, নাম বেইজ থিয়রেম, সাঙ্কেতিক ভাষায় লিখলে যাকে দেখতে লাগে এইটুকু নিরীহ এক-লাইনের ফর্মুলাঃ P(A|B) = (P(B|A)P(A))/P(B)। কিন্তু এই P(A|B) জিনিষগুলো কি?
এই সংখ্যাগুলোর গালভরা নাম কন্ডিশনাল প্রোবাবিলিটি, সহজ কথায় বলতে গেলে প্রোবাবিলিটি মানে সম্ভাবনা, আর বেইজ থিয়োরেম বলে দেয় কীভাবে নতুন তথ্য পেলে সেই সম্ভাবনা-টা পালটে যাবে। মানে ধরুন আপনি সুপার লোটোর টিকিট কেটেছেন, তিন জোড়া সংখ্যা মিলে গেলেই কোটিপতি হবেন, কিন্তু আপনি মনে মনে জানেন মিলে যাওয়ার চান্স খুব-ই কম, প্রায় নেই বললেই চলে। তাও টিভিতে লটারির ড্র দেখতে বসলেন, আর কি কাণ্ড, প্রথম দুটো নম্বর মিলেছে! আপনি লাফিয়ে উঠেছেন কি ওঠেননি, অমনি লোডশেডিং। এইবার প্রশ্ন হলো, এই যে আপনি জেনে গেলেন তিন জোড়ার মধ্যে এক জোড়া নম্বর মিলেছে, তাহলে নিশ্চয়ই আপনার লোটোপতি হওয়ার চান্স আগের থেকে বাড়লো? ঠিক কতটা বাড়লো?
ঠিক এই অঙ্কটাই করতে সাহায্য করে কন্ডিশনাল প্রোবাবিলিটি। কিছু না জেনেই যে সম্ভাবনা ছিলো তিন জোড়া অঙ্ক মেলার, সেটাকে আমরা বলি “প্রায়োর প্রোবাবিলিটি”, আর যেই ডেটা পেলেন, আপডেট করলেন, সেই নতুন প্রোবাবিলিটির নাম “পস্টেরিয়র”। আর যে সূত্রে এরা দুজন জোড়া সেইটাই ওই উপরের বেইজ থিয়োরেম।
ফিরে যাই ব্লাড টেস্টের ল্যাবোরেটরিতে। এইখানে আমরা যেটা আসলে জানতে চাই সেটা হচ্ছে ‘পজিটিভ রেজাল্ট আছে ধরে নিয়ে অসুখ থাকার সম্ভাবনা কত? এইটাই অঙ্কের সঙ্কেতে লিখলে, P(অসুখ আছে | পজিটিভ রেজাল্ট), অসুখের ‘কন্ডিশনাল প্রোবাবিলিটি’। (মাঝের ঐ দাঁড়িটার নাম গিভেন-দ্যাট, মানে ধরে নিয়ে)। এখানেও সেই আগের মতন, যদি কোনো টেস্ট না করান, তাহলে অসুখ হওয়ার যে সম্ভাবনা সেইটা আমাদের ‘প্রায়োর’, আর যেই নতুন একটা তথ্য পেলেন (পজিটিভ টেস্ট রেজাল্ট), তাহলে সম্ভাবনা বেড়ে যত হলো, সেইটাই ‘পস্টেরিয়র’। এই অঙ্কটা এবারে কষা যাক।
বেইজ থিয়রেমটা আরেকবার দেখে নিন। ওই সূত্রে বসিয়ে এইটাই বের করতে গেলে, ঐ A, B র জায়গায় ‘অসুখ’ আর ‘পজিটিভ টেস্ট রেজাল্ট’ বসান, দাঁড়াবে এই -
এইবারে Pপজিটিভ, অর্থাৎ সবাইকে ধরে পজিটিভ রেজাল্টের প্রোবাবিলিটি কি? তাহলে জানতে হবে তিনটে জিনিস।
১) সত্যিকারের অসুখ থাকলে পজিটিভ রেজাল্ট আসার প্রোবাবিলিটি কত, ধরে নেওয়া যাক টেস্ট-টি খুব-ই উন্নতমানের, এবং এই প্রোবাবিলিটি-টি একের কাছে, ধরলাম ৯৯% বা ০.৯৯।
২) সুস্থ মানুষের ক্ষেত্রে ভুল করে পজিটিভ আসার প্রোবাবিলিটি কত? এই দ্বিতীয় সংখ্যাটাই ওই ‘ফলস পজিটিভ রেট’ অর্থাৎ ০.১%, আর
৩) অসুখটা কত রেয়ার বা কতটা কমন? মানে সে কি খুব আনকমন একটা জেনেটিক ডিজ-অর্ডার (যা মাত্র ১% লোকের হয়), না কি হাঁচি-কাশি কিম্বা পেটের ব্যামো? ধরে নেওয়া যাক, অসুখ-টা ভয়ানক বিরল, হয় দশ হাজারে এক জনের – মানে P(অসুখ) = ১/১০,০০০ = ০.০০০১ (এইটাই আমাদের তথাকথিত প্রায়োর প্রোবাবিলিটি)। গোটা ব্যাপার-টা নীচে দেখানো ফ্লো-চার্টের মত করে ভাবা যায়।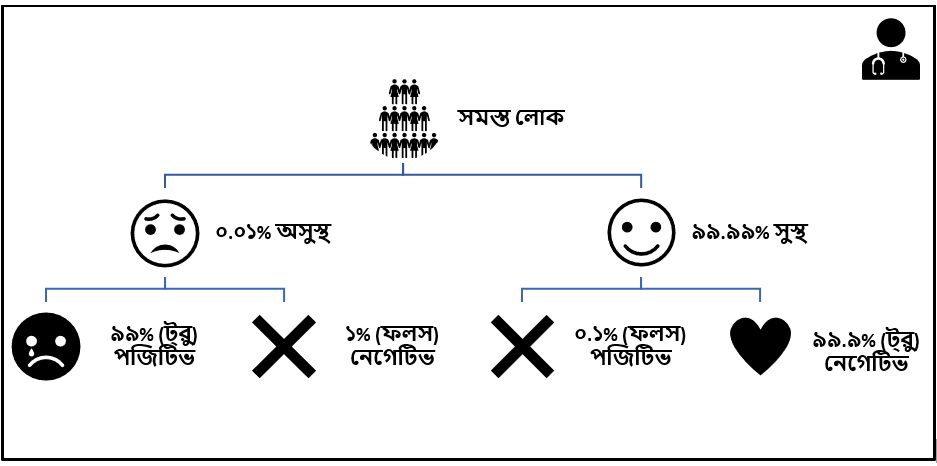
এইবারে আপনি লিখে ফেলতে পারবেন যে সব-মিলিয়ে পজিটিভ হওয়ার প্রোবাবিলিটি, অর্থাৎ হচ্ছে সুস্থ-অসুস্থ দুইয়ের মিলিয়ে টোটাল প্রোবাবিলিটিঃ
এইবারে ফিরে যাই বেইজের কাছে, একদম উপরের ফর্মুলায় এই নম্বর-টা বসালে কী মেলে?অর্থাৎ, ১০% এর থেকে সামান্য কম। মানে যদি অসুখ-টা সত্যি অতো রেয়ার হয়, তাহলে পজিটিভ আসা সত্ত্বেও, এবং এই এতো ভালো ফলস পজিটিভ, ফলস নেগেটিভ রেট নিয়েও আপনার অসুখ থাকার চান্স কত? মাত্র ১০%।
আশার কথা এই যে, অসুখ অতো বিরল না হলেই এই ব্যাপারটা আর গোলমেলে থাকে না। ধরি যদি ১০০ জনে এক জনের অসুখ-টা হয়, তাহলে? উপরের এক-ই ফর্মুলায় নাম্বারগুলো পালটে নিন, উত্তর আসবে ০.৯০৯০… মানে বেশ ভালোই সম্ভাবনা যে অসুখটা সত্যি বাধিয়েছেন। বলাই বাহুল্য ইচ্ছে করেই অসুখের নাম কোভিড, আর টেস্টের নাম আর-টি-পিসিয়ার দিইনি, কারণ উপরের ঐ ১, ২ আর ৩ এর মধ্যে ১ আর ৩ আমার অজানা।
দুঃখের কথা এই যে এইটা এক্কেবারে বইয়ের অঙ্ক-ই যে শুধু এমনটা নয়। খুব বিরল অসুখ, যেমন ভ্রূণস্থ শিশুর ক্রোমোজোমাল অ্যানোম্যালির একটি অসুখের অ্যান্টিনেটাল স্ক্রিনিং-এর ফলস পজিটিভ রেট মাত্র ০.১%, কিন্তু সে অসুখ এতোই রেয়ার যে পজিটিভ-দের মধ্যে সত্যি সুস্থ হওয়ার সম্ভাবনা অনেক বেশি – ৪৫-৯৪%।২ থিয়োরেম-টা ছোট্ট। কিন্তু প্রভাব অনেকদূর। কোর্টরুম থেকে ক্লিনিক থেকে ক্লাসরুম। এর সঙ্গে জড়িত সবথেকে কুখ্যাত প্যারাডক্স-টির নাম “প্রসিকিউটর’স ফ্যালাসি”, যার অপপ্রয়োগের বলি হয়েছেন অনেক, অনেকজন, এবং হয়তো হবেন-ও আরও অনেকে।
কী সেই ফ্যালাসি? খুব সহজ করে বললে, দুই প্রকার কন্ডিশনাল প্রোবাবিলিটির মধ্যে গুলিয়ে ফেলা, একটি P(প্রমাণ | দোষ), আর অন্যটি P(দোষ | প্রমাণ), একটা উদাহরণ দিলে স্পষ্ট হয়ে যাবে।
ধরে নিন আপনি আগাথা ক্রিস্টির গল্পের একটা চরিত্র, ছুটিতে একটা দ্বীপে বেড়াতে গেছেন সেই দ্বীপে আপনাকে নিয়ে মোট ১০০০ জন লোক। সকালে উঠে দেখা গেলো একজন খুন হয়েছেন, আর মসিয়েঁ পোয়ারোর সন্দেহের তির আপনার দিকে। এবং এও জানা গেলো যে আপনার আর খুনীর রক্তের গ্রূপ এক- এমন একটা গ্রূপ (ধরলাম G) যা থাকে মোটে ১০% লোকের থাকে। এই পর্যন্ত তথ্যের ভিত্তিতে যদি পোয়ারো বলেন, আপনার-ই খুনী হওয়ার সম্ভাবনা ৯০%, তাহলে কি উনি ঠিক?
উত্তর হচ্ছে, নাঃ, একেবারেই না।
একটু ভেবে দেখি। ১০% লোকের ব্লাড গ্রূপ G হলে, ওই দ্বীপেই আছেন এমন ১০০ জন মানুষ, এবং পোয়ারোর আর কোনো কারণ নেই কাউকে বেশী বা কম সন্দেহ করার। এখন যদি আপনার বিরুদ্ধে প্রমাণ শুধুমাত্র ঐ ম্যাচিং ব্লাড গ্রূপ হয় তাহলে আপনার দোষী হওয়ার সম্ভাবনা মাত্র ১০০-এ ১, অর্থাৎ ১% !! (বলাই বাহুল্য, পোয়ারো এমন ভুল করবেন না।)
এই যে আপনার খুনি হওয়ার সম্ভাবনা নেমে গেলো ৯০% থেকে ১%-এ, এইটার-ই নাম প্রসিকিউটর’স ফ্যালাসি।
আরেকটু জটিল একটা অঙ্ক দেখে নিই। ধরা যাক, সেই গল্পের দ্বীপেই আছেন আপনি, কিন্তু গোয়েন্দা এখন ৫০% নিশ্চিত যে আপনি-ই আসামী। এইবার আগেই জানি যে আপনার এমন একটি বৈশিষ্ট্য আছে যেটা অপরাধীর-ও ছিলো বলে প্রমাণিত, আর এও জানা আছে যে গোটা জনসংখ্যার মাত্র ১০%-এর সেই বৈশিষ্ট্য আছে। তাহলে এখন প্রোবাবিলিটি কত যে আপনি-ই অপরাধী?
আবার যদি আরও এক ধাপ এগিয়ে জানা যায়, ফরেন্সিক প্রমাণ পাওয়া গেছে, যা আরও অনেক অনেক গুণে মেলার সম্ভাবনা কম, কোটিকে গুটিক, তাহলেই বা কী হবে?
আবার সেই বেইজ থিয়োরেমের গল্প! এইবারে A, B-এর জায়গায় অসুখ আর টেস্টের রেজাল্ট না বসিয়ে বসান, প্রমাণ (E) আর দোষী (G) অথবা নির্দোষ (I)। যদি ধরে নিই পপুলেশনের মধ্যে ওই বৈশিষ্ট্য খুব বিরল নয়, মানে ১০%, তাহলেও দোষী হওয়ার কণ্ডিশনাল প্রোবাবিলিটি বেড়ে হয়ে যাবে প্রায় ৯১%, আর যদি ধরি অত্যন্ত বিরল বৈশিষ্ট্য, যথা ডিএনএ বা ফিঙ্গারপ্রিন্ট? চট করে দেখানো যায়, যে যত বিরল হবে (অর্থাৎ একজন নির্দোষ লোকের ওই এক-ই বৈশিষ্ট্য থাকার সম্ভাবনা যতই শূন্যের দিকে যাবে), তত সন্দেহভাজনের দোষী হওয়ার সম্ভাবনা যাবে ১০০%-এর দিকে।
সহজ একটা ফর্মুলা দেওয়ার লোভ সামলাতে পারছি না। ধরে নিই যে নির্দোষ লোকের মধ্যে অপরাধীর একটি বিশেষ বৈশিষ্ট্য থাকার সম্ভাবনা w আর ধরে নিই যে গোয়েন্দার সন্দেহ যে আপনিই দোষী p (অর্থাৎ গোয়েন্দার প্রায়োর প্রোবাবিলিটি p), তাহলে কণ্ডিশনাল প্রোবাবিলিটি,
P(দোষ | বৈশিষ্ট্য) = 1/ (1 + w*(1-p)/p)
যদি বৈশিষ্ট্যটি বিরল হয়, w শূন্যের দিকে যাবে, আর যদি আপনার উপরে সন্দেহ তীব্র হয়, তাহলে p যাবে ১-এর দিকে আর 1-p শূন্যের দিকে, এবং দুই ক্ষেত্রেই আপনার কেস খাওয়ার প্রোবাবিলিটি সোজা ১০০% দিকে ছুটবে।
মুশকিল এই যে বাস্তবের কোর্টকাছারি থেকে গোয়েন্দা-গল্পে ঐ দুটো প্রোবাবিলিটি গুলিয়ে ফেলা – P(E | G) আর P(G | E), খুব-ই নিত্য ঘটনা, বলাই বাহুল্য বেইজ-বাবুর পর আড়াইশো বছর কেটে গেলেও আমরা তার থিয়োরি এখনো শিখে উঠতে পারিনি ঠিক করে।
সেইরকম দু-একটি সত্যিকারের উদাহরণ দিয়ে প্রসিকিউটর-র ফ্যালাসির গল্প শেষ করতে চাই।
সবচাইতে বিখ্যাত গল্পটি ও-জে-সিম্পসনের। বিখ্যাত আমেরিকান ফুটবলার (সকার নয় কিন্তু)। ও-জে-সিম্পসন নিজের স্ত্রীকে খুন করার অভিযোগে গ্রেপ্তার হন, বহুদিন ধরে বহুল-চর্চিত ট্রায়াল হয় তার, সে ট্রায়ালের সম্প্রচার হয় সারা আমেরিকা জুড়ে টেলিভিশনে। এবং আশ্চর্যজনকভাবে, প্রথমবার ট্রায়ালে গুচ্ছ গুচ্ছ প্রমাণ থাকা সত্ত্বেও ছাড় পেয়ে যান ওজে। প্রসিকিউশন প্রমাণ এনে দেন ওজে নিজের স্ত্রীকে মারধোর করতেন, কিন্তু ডিফেন্স অ্যাটর্নি অ্যালান ডেরশোউইজ সওয়ালে বলেছিলেন, তাতে কী? প্রতি ২৫০০-এ নির্যাতনকারীর ১ জন খুন করেন শেষমেশ। জুরির লোকেরা একটু বেইজ থিয়োরেম জানলেই দেখতে পেতেন এই তথ্য বরং প্রমাণ করে যে ওজে সিম্পসনের দোষী হওয়ার সম্ভাবনা ৯০% এর উপরে!
যেমন দুঃখের গল্প স্যালি ক্লার্কের – যে মহিলার পরপর দুটি সন্তান মারা যায় (সাডেন ইনফ্যাণ্ট ডেথ সিনড্রোম) SIDS-এ। ১৯৯৯ সালে আদালত তাকে দোষী সাব্যস্ত করে এই প্রোবাবিলিটির ভিত্তিতে, যে যদি ধূমপান করেন না এবং ২৫-এর উপরে বয়েস এমন একটি পরিবারে সিডসের সম্ভাবনা হয় ৮৫০০-এ ১, তাহলে দুজন সন্তানের মৃত্যুর সম্ভাবনা (১/৮৫০০)*(১/৮৫০০০), মানে ৭৩ মিলিয়নে ১। চার বছর পরে, রে হিল নামে একজন অঙ্কের প্রোফেসর প্রোবাবিলিটি কষে দেখান যে একাধিক ভুল ছিলো এই যুক্তিতে। প্রথমতঃ, দুটি সন্তানের সিডস রোগ ইন্ডিপেন্ডেন্ট নয়, অর্থাৎ একজনের সিডসে মৃত্যু ধরলে, দ্বিতীয়জনের প্রোবাবিলিটি ১/৮৫০০ থাকে না, হয় অনেক বেশী ১/১০০, আর দ্বিতীয়তঃ, একজন মানুষের দুজনকে খুন করার (অর্থাৎ ডাবল হোমিসাইডের) প্রায়োর প্রোবাবিলিটি খুব-ই কম, এমনকি সিডসের থেকেও অনেক অনেক কম।
স্যালি ক্লার্ক শেষমেশ ছাড়া পান ২০০৩ সালের ২৯শে জানুয়ারী। যদিও দীর্ঘ তিন বছরের কারাদণ্ড, সন্তান-হারানোর শোক – এই সব মিলিয়ে তখন তিনি মানসিক ভারসাম্যহীন। মাত্র চার বছর পরেই ২০০৭ সালে, মাত্র ৪২ বছর বয়সে, অ্যালকোহলিক পয়েজনিং-এ মারা যান প্রাক্তন সলিসিটর, স্যালি ক্লার্ক।
৩
শেষতম উদাহরণ, লাই ডিটেকটর, যার ভালো নাম পলিগ্রাফ। উইলিয়ম মল্টন মারস্টনের এই ১৯২২ সালের আবিষ্কার পরীক্ষা করা হয় এক কৃষ্ণাঙ্গ যুবকের উপরে, যার নাম জেমস অ্যালফান্সো ফ্রায়ার, খুন ও ডাকাতির অভিযোগে যাকে গ্রেপ্তার করা হয়েছিলো সেই সময়েই।

কিন্তু লাই ডিটেকটর-ও তো সেই ব্লাড টেস্টের মত, তাই না? তার-ও তো ফলস পজিটিভ, ফলস নেগেটিভ আছে? যেমন এই পেপারে বলা, (“Accuracy estimates of the CQT range from 74% to 89% for guilty examinees, with 1%to 13% false-negatives, and 59% to 83% for innocent examinees, with a false-positive ratio varying from 10% to 23%…”), অর্থাৎ গড় করলেও ফলস পজিটিভ রেট প্রায় ১৭% আর ফলস নেগেটিভ প্রায় ৮% এর কাছাকাছি। যদি সঙ্গে আরও ধরে নিই যে, পৃথিবীতে মিথ্যেবাদীর সংখ্যা খুব বেশী নয়, বরং, খুব বড়ো মিথ্যে কথা বলার সম্ভাবনা আরই কম, তাহলে ঐ যোগ-ভাগ করে দেখা যাবে, কন্ডিশনাল প্রোবাবিলিটি P(মিথ্যেবাদী | লাই-ডিটেক্টরে পজিটিভ) মোটেও এমন কিছু বেশী নয়, ঐ ৫০% মানে আন্দাজে ঢিল ছোঁড়ার আশেপাশেই ঘুরঘুর করছে। উল্টোটা, মানে নেগেটিভ এলে সত্যি বলার প্রোবাবিলিটি? সেও ওইরকম-ই।
সেইদিনকার জাজসাহেব, জাস্টিস ম্যাককয়, লাই ডিটেক্টরের রেজাল্ট-কে প্রামাণ্য তথ্য হিসেবে স্বীকৃতি দেননি, এবং সেইদিন থেকে এখনও অব্দি লাই ডিটেক্টরের রেজাল্ট আদালতে ‘ইনঅ্যাডমিসিবল’।
আর সেই যে উইলিয়ম মল্টন মারস্টন, লাই ডিটেকটর যাঁর মস্তিষ্কপ্রসূত যন্ত্র, তিনি ছিলেন এক ভয়ানক ইন্টারেস্টিং চরিত্র, কিছুটা ধূসর-ও বটে। ইতিহাসের পাতায় তিনি অমর থেকে গেছেন তাঁর অন্য একটি কীর্তির উপর দাঁড়িয়ে। পরের জীবনে কমিক বুক লেখক এই মারস্টনের-ই সৃষ্টি চরিত্র “ওয়ান্ডার উওম্যান”, এখন ডিসি কমিক্সের কল্যাণে যাকে চেনে বাচ্চাবুড়ো থেকে সব্বাই।
ওয়ান্ডার উওম্যানের আসল অস্ত্রটি কী জানেন? ল্যাসো অফ ট্রুথ। যেইটি দিয়ে অপরাধীদের পেঁচিয়ে ধরলে তারা বাধ্য হন হড়হড় করে সব সত্যি কথা কবুল করে নিতে।
ওয়ান্ডার উওম্যান ও ল্যাসো অফ ট্রুথভেবে দেখুন সুধী পাঠক, নিছক সমাপতন?
(পুনশ্চঃ টিউশনি-তে এসে পড়েছেন যখন, একটা হোমওয়ার্ক নিয়ে যান। এমন একজন বিখ্যাত বাঙালি গোয়েন্দার নাম বলুন যার গল্পে প্রসিকিউটর’স ফ্যালাসির ভুল আছে। আর বোনাস, কোন গল্প বলতে পারলে আপনাকে একটা জনাইয়ের মনোহরা খাওয়াবো।)
সূত্রঃ
প্রসিকিউটর-স ফ্যালাসি নিয়ে পড়তে গেলে যে কোনো বাচ্চাদের প্রোবাবিলিটির টেক্সট খুলে কন্ডিশনাল প্রোবাবিলিটি অথবা বেইজ থিয়োরেমের জায়গাটা পড়ে নিন। বাকি সব মানুষ-ই বিখ্যাত বা কুখ্যাত, ওজে সিম্পসন, স্যালি ক্লার্ক, উইলিয়ম মারস্টন ও জেমস ফ্রায়ার – এদের সবার নামে গুগল সার্চ করলেই গুচ্ছখানেক পেপার ও উইকি আর্টিকল পাবেন, যে কোনো একটা ধরে সিধে পড়তে শুরু করে দিন।
পুনঃপ্রকাশ সম্পর্কিত নীতিঃ এই লেখাটি ছাপা, ডিজিটাল, দৃশ্য, শ্রাব্য, বা অন্য যেকোনো মাধ্যমে আংশিক বা সম্পূর্ণ ভাবে প্রতিলিপিকরণ বা অন্যত্র প্রকাশের জন্য গুরুচণ্ডা৯র অনুমতি বাধ্যতামূলক।প্রথম কিস্তি | দ্বিতীয় কিস্তি | তৃতীয় কিস্তি | চতুর্থ কিস্তি | পঞ্চম কিস্তি | ষষ্ঠ কিস্তি | সপ্তম কিস্তি | অষ্টম কিস্তি | সমষ্টি থেকে ব্যষ্টি | ভক্স পপুলি | দুই লেজান্ড্রর গল্প | বিষের ইতিহাস, ইতিহাসের বিষ - আরও পড়ুনরাধিকা ও আর্শোলা - যদুবাবুআরও পড়ুনসিম্পসন’স প্যারাডক্স - যদুবাবুআরও পড়ুনমধুবাতা ঋতায়তে - শারদা মণ্ডলআরও পড়ুনদিন গোনার দিন ৭ - হীরেন সিংহরায়আরও পড়ুনমধুবাতা ঋতায়তে - শারদা মণ্ডলআরও পড়ুনঅন্তর্বাসঃ গল্প - রানা সরকারআরও পড়ুনদ্য প্যারাডাইস - Anirban Mআরও পড়ুনআয়না - Anjan Banerjeeআরও পড়ুনঈশ্বরের বরপুত্র - Ranjan Roy
- মতামত দিন
-
বিষয়বস্তু*:
-
যদুবাবু | ০৯ মে ২০২১ ০১:৪৪105721
Erratum: একটা ফর্মুলা কোনোভাবে দুবার এসে গেছে। আমি নীচে অজ্জিনাল-টা দিয়ে দিলাম। এটা ঐ ফ্লো-চার্টের পরের জায়গাটা।
যাইহোক, ঐ ফর্মুলা বা অঙ্ক-কষা/ক্যালকুলেশন-টা এমনিও সেই ভাবে দরকারী নয়, কিন্তু যদি কারুর খটকা লাগে সেই ভেবে ক্ল্যারিফাই করলাম এই আর কী।
 dc | 171.49.***.*** | ০৯ মে ২০২১ ০৮:০৩105728
dc | 171.49.***.*** | ০৯ মে ২০২১ ০৮:০৩105728সকাল সকাল যদুবাবুর পোস্ট পড়তে ভারি ভালো লাগলো। একটা পয়েন্ট মনে করিয়ে দি, তাহলে বোধায় লেখাটা আরেকটু পরিষ্কার হবে। বেজ থিওরেম ডিপেনডেন্ট ইভেন্টের ক্ষেত্রে ব্যবহার করা হয় (নামের মধ্যেই আছে, কন্ডিশনাল প্রোবাবিলিটি।
দুরকম প্রোবাবল ইভেন্ট হতে পারে, ইন্ডিপেনডেন্ট আর ডিপেনডেন্ট। ধরুন আপনি একটা কয়েন টস করলেন, হেড পেলেন। আবার টস করলেন আবার হেড পেলেন। আবার টস করলেন, টেল পেলেন। এই প্রতিটা টস একটা করে ইন্ডিপেনডেন্ট ইভেন্ট, অর্থাত একটা টসের আউটকাম (হেড না টেল) অন্য ইভেন্টের ওপর ডিপেন্ড করে না। অর্থাত ধরুন একটা আনবায়াসড কয়েন টসে হেড পাওয়ার সম্ভাবনা ০।৫, আপনি পরপর দশবার টস করে দশবার হেড পেলেন (ধরে নিচ্ছি আনবায়াসড কয়েন)। তাহলে ১১ তম টসে হেড পাওয়ার সম্ভাবনা কতো? সেটা কিন্তু ০।৫ ই থাকবে, বদলাবে না। এটা আমাদের লাইফে একটা খুব পরিচিত ফ্যালাসি, অর্থাত কোন একটা ইন্ডিপেনডেন্ট ইভেন্ট বারবার ঘটে, তো কয়েকবার যদি বাই চান্স কোন একটা আউটকাম হয়, তো আমরা ধরে নি পরবর্তীতেও সেই একই আউটকাম হবে। যদি তা না হয় তো আমরা ভয়ানক অবাক হয়ে যাই।
এর ঠিক উল্টো হলো বেজ থিওরেম, যেখানে একটা চেন অফ ডিপেনডেন্ট ইভেন্টের সম্ভাবনা মাপা হয়। এগুলো সবাই জানেন, তাও একটু মনে করিয়ে দেওয়া :-)
 dc | 171.49.***.*** | ০৯ মে ২০২১ ০৮:০৮105729
dc | 171.49.***.*** | ০৯ মে ২০২১ ০৮:০৮105729আর উইলিয়ম মল্টন মারস্টন ইন্টারেস্টিং চরিত্র বললে কমই বলা হয়। একবার ওনার জীবনকাহিনী পড়েছিলাম।
-
যদুবাবু | ০৯ মে ২০২১ ০৯:১৪105738
@dc: থ্যাঙ্ক ইউ !! আপনি পড়লেন খুব আনন্দ হলো।
ইন্ডিপেন্ডেন্ট ইভেন্টের কথা লেখা উচিত ছিলো, আমি ঐ স্যালি ক্লার্কের ঘটনা লেখার সময়েই ভাবছিলাম, এই যে বললাম ইন্ডিপেন্ডেন্ট নয় কাজেই প্রোবাবিলিটি p^2 হবে না, এটাই তো আগে ব্যাখ্যা করা নেই, তারপরে তালেগোলে লিখতে ভুলে গেলাম, তবে এইটা রিভাইজ করলে ইন্ডিপেন্ডেন্সের কথা লিখবো। এর পরের কোনো একটা কিস্তিতে ইন্ডিপেন্ডেন্স নিয়ে আরেকটু গুছিয়ে লিখবো। স্ট্যাটিস্টিকাল সুইন্ডলস - মানে ঐ যে হাজারে হাজারে র্যান্ডম গেস করলেও একটা মিলে যাবে সেইটা নিয়ে যে একরকমের লোক-ঠকানো ব্যবসা হয় সেটাও লেখার ইচ্ছে আছে।
মারস্টন সাংঘাতিক লোক, তাই না? ওনাকে নিয়ে একটা ফিল্ম আছে, সেটা দেখার মতন। বইটা পড়িনি, খুঁজে পেলে নামটা বলবেন?
ফিল্মটা এইটাঃ https://www.netflix.com/title/80195940
 dc | 171.49.***.*** | ০৯ মে ২০২১ ০৯:৪৭105740
dc | 171.49.***.*** | ০৯ মে ২০২১ ০৯:৪৭105740যদুবাবু অনেক ধন্যবাদ, সিনেমাটা দেখবো।
হ্যাঁ, ইনডিপেনডেন্ট র্যান্ডম গেসিং নিয়ে প্রচুর লোক ঠকানো হয়। বলতে গেলে পুরো জ্যোতিষী ব্যাপারটাই এর ওপর দাঁড়িয়ে আছে। একজনের ক্ষেত্রে জ্যোতিষীর প্রেডিকশান কোনভাবে মিলে গেলেই তাকে দেখিয়ে আরও কয়েকজনকে পাকড়াও করা হয়।
-
 Anindita Roy Saha | ১২ মে ২০২১ ১৯:৪০105897
Anindita Roy Saha | ১২ মে ২০২১ ১৯:৪০105897 সাগ্রহে পড়লাম। রাশি বিজ্ঞানে কিছুটা উৎসাহ আছে বলে হিসেব করার চেষ্টা করা গেল।
পোয়ারোর সম্ভাব্য গল্পের উদাহরণ প্রসঙ্গেএকটি প্রশ্ন রইলো।
বেইজ থিওরেম দিয়ে ১% এ নেমে আসার হিসেব মিলছে। ট্রি ডায়াগ্রাম (ফ্লো চার্ট না ট্রি?) এঁকে প্রোবাবিলিটি কষা গেল।
কিন্তু সম্ভাব্য ভুলের ৯০% কীভাবে এলো বুঝতে পারলাম না। এটা কি ১০% হবে?
অর্থাৎ ফ্যালাসি ১০% থেকে ১% করে দেবে , এমনই তো মনে হচ্ছে।
-
যদুবাবু | ১৩ মে ২০২১ ০৮:২৩105909
দারুণ ব্যাপার তো। আজকেই আমাকে দুজন বন্ধু বলেছে 'জটিল' বলে কেউ পড়বে না। আপনি পড়েছেন + প্রশ্ন করেছেন এতে অত্যন্ত খুশি।
আপনার উত্তরটা দেওয়ার একটা অপচেষ্টা করি। আসলে আমরা যারা এই ফ্যালাসিটায় ভুগি না, তাদের পক্ষে ফ্যালাসিয়াস আরগুমেন্ট ফ্রেম করা খুব শক্ত। কিন্তু লোকে যেটা বলে ব'লে শুনেছি - তা এই যে, কৌঁসুলি / গোয়েন্দা জিগ্যেস করবেন, "what is the chance that an innocent man shares the trait?" - তার উত্তর ঐ দশ পারসেন্টের কাছাকাছি কারণ দশ পারসেন্ট লোকের-ই আছে (একজন-কে বাদ দিলেও ৯.৯%)। সেখান থেকে ভুল করে বলা তাহলে বাকি প্রোবাবিলিটি - অর্থাৎ - ৯০% - যে যার উপরে সন্দেহ সেই অপরাধী। (মানে এটা আগাগোড়াই ভুলভাল লজিক, কিন্তু হয়তো এইভাবে ভুল হতে পারে বলে লোকে বলে থাকে।)
আবার আপনি যেটা বলছেন সেটাও তো হতেই পারে। মানে ওইভাবেও ভুল হতেই পারে। সেটাও তো ফ্যালাসি এবং প্রসিকিউটরের-ই দোষ। :)
 Anindita Roy Saha | 160.202.***.*** | ১৩ মে ২০২১ ২১:১৯105941
Anindita Roy Saha | 160.202.***.*** | ১৩ মে ২০২১ ২১:১৯105941উত্তরের জন্য ধন্যবাদ।
আরেকটি হিসেব কষে গোলমাল মনে হচ্ছে।
ডিনোমিনেটরে টোটাল প্রোবাবিলিটি বোধ হয় ।
০.৯৯*০.০০০১ ০.৯৯৯৯*০.০০১=০.০০১০৯৮৯
এর ফলে পোষ্টেরিওর প্রোবাবিলিটি হয়ে যাচ্ছে ০.০৯০০৯ অথবা ৯ %
 Anindita Roy Saha | 160.202.***.*** | ১৩ মে ২০২১ ২১:৫৭105942
Anindita Roy Saha | 160.202.***.*** | ১৩ মে ২০২১ ২১:৫৭105942টাইপিং সমস্যায় + বাদ পড়েছে। তবে আপনি অবশ্যই বুঝতে পেরেছেন।
 Abhyu | 198.137.***.*** | ১৩ মে ২০২১ ২২:২৬105944
Abhyu | 198.137.***.*** | ১৩ মে ২০২১ ২২:২৬105944 dc | 171.49.167.195 | ০৯ মে ২০২১ ০৮:০৩
dc | 171.49.167.195 | ০৯ মে ২০২১ ০৮:০৩নরেন্দ্রপুরের এক ছোঁড়া, আমার কয়েন টসিং উদাহরণের উত্তরে বলল হ্যাঁ হ্যাঁ বুঝে গেছি, ঐ জয়েন্ট দেবার মত, যত বারই দে পাবার প্রোব্যাবিলিটি একই থাকে। বলে "জয়েন্ট পাবো কি পাবো না ভেবে ভেবে হায়রে পাওয়া তো হল না, হায়" গাইতে গাইতে বাথরুমে ঢুকে গেল।
-
যদুবাবু | ১৪ মে ২০২১ ০২:০৫105946
অনিন্দিতাঃ আমার প্রথম কমেন্ট দেখুন - ডিনমিনেটরে টোটাল প্রোবাবিলিটি কষে দেওয়া আছে। তবে তারপরের স্টেপে ভাগ করার সময়ে একটু ভুল রয়ে গেছে। কোনো কারণে বাংলা-ইংরেজি ফর্মুলা ওয়ার্ড থেকে এই এডিটরে টাইপ/ট্রান্সফার করতে গিয়ে এদিক-ওদিক কিছু শূন্য উড়ে গেছে এবং দু-দুবার এক-ই ফর্মুলা বসেছে। তাতে খুব বেশী গল্পটা পালটায় না, কিন্তু তাও পস্টেরিয়র প্রোবাবিলিটি ঐ ৯.০০৯%-ই হবে। অর্থাৎ, যেটা প্রায় ১০% লিখেছি, ওটা ৯% হবে। এই লেখাটা এডিট করার উপায় নেই তবে রিভাইজ করার সময় এইটা ঠিক করে নেবো। ধন্যবাদ।
অভ্যু-দাঃ জয়েন্ট শুনে একটু পুরোনো ব্যথা চেগে উঠলো। তবে একটাই শব্দ যে কৈশোরে বিভীষিকা আর যৌবন অনওয়ার্ডস তূরীয় আনন্দের কারণ হতে পারে, তা 'জয়েন্ট' না পেলে বোঝার উপায়-ই থাকতো না।
-
যদুবাবু | ১৪ মে ২০২১ ০২:৫৭105947
@অনিন্দিতাঃ আর একটা কথাও না বললে অন্যায় হবে, আমি এই পুরো আর্টিকল-টা লিখতে লিখতে বারংবার ভেবেছি যে ধুর এই সব কেউ পড়বে না, কারুর-ই আগ্রহ হবে না, কারণ এক, যতোটা সহজ করা যেতো আমি করতে পারিনি আর দুই, স্ট্যাট/অঙ্ক ইত্যাদির প্রতি মানুষের অকারণ ভীতি ইত্যাদি।
আপনি পড়েছেন এবং একাধিক জায়গায় ত্রুটি-বিচ্যুতি ধরেছেন - এ জন্যে অনেক অনেক ধন্যবাদ ! আর পরের আর্টিকেল-টা লেখার সময় অবশ্যই এই 'সিলি মিসটেক'গুলো এড়াতে চেষ্টা করবো।
আরও কী কী করলে লেখার প্রেজেন্টেশন ভালো হবে, সেইসব-ও অবশ্যই বলুন - আমার একেবারেই হাতপাকানো লেখা, আস্তে আস্তে জট খুললে খুব-ই আনন্দ হবে।
-
অরিন | ১৪ মে ২০২১ ১০:০২105949
অনবদ্য যদুবাবু, অনবদ্য! সাধু!
 Anindita Roy Saha | 160.202.***.*** | ১৪ মে ২০২১ ২০:২৮105976
Anindita Roy Saha | 160.202.***.*** | ১৪ মে ২০২১ ২০:২৮105976আপনার এ জাতীয় অন্যান্য লেখাও পড়েছি। ক্লিওপেট্রা আর যুদ্ধ বিমান খুব ভালো লেগেছিল। এই ধরনের গাণিতিক আলোচনা মস্তিষ্কের জন্য অতি উপাদেয় খাদ্য। আরো লিখুন , সঙ্গে আছি।
-
যদুবাবু | ১৫ মে ২০২১ ০৫:৫২105989
অরিন-দা, অজস্র ধন্যবাদ !! এখানে তো ট্যাগ করা যায় না (ভাগ্যিস যায় না!), কিন্তু ইচ্ছে করছিলো আপনাকে ডেকে পড়াই। :)
অনিন্দিতাঃ :) ... ইচ্ছে আছে, দেখি !
-
অরিন | ১৫ মে ২০২১ ১০:১৭105995
যদুবাবু, আপনার অনবদ্য লেখাটি পড়ে দু-একটি কথা লেখার ইচ্ছে হল, এখানে লিখে রাখি, দেখি আপনি কি বলেন। আপনি অসুখের ডায়গনসিস দিয়ে শুরু করেছেন, আমাদের মধ্যে যাঁরা ডাক্তার তাঁরা জ্ঞানত বা (অজ্ঞানবশতই ধরুন), বেইসিয়ান প্রায়র বিলিফ পোস্টিরিয়র বিলিফ কাজে ব্যবহার করি | আপনি যাকে বললেন প্রায়র প্রোবাবিলিটি, আমরা তাকে Odds এ পরিণত করে বলি প্রায়র বিলিফ, তার অডস | আমরা যদি কারো প্রোবাবিলিটি P(X) দিয়ে বোঝাই, তাহলে তার Odds হবে,
Odds(X) = P(X) / (1 - P(X))
এই হিসেবে
P(X) = Odds(X) / (1 + Odds(X))
য়েমন ধরুন আপনি যে অসুখটির কথা লিখেছেন,
---
তিনটে জিনিস।
১) সত্যিকারের অসুখ থাকলে পজিটিভ রেজাল্ট আসার প্রোবাবিলিটি কত, ধরে নেওয়া যাক টেস্ট-টি খুব-ই উন্নতমানের, এবং এই প্রোবাবিলিটি-টি একের কাছে, ধরলাম ৯৯% বা ০.৯৯।
২) সুস্থ মানুষের ক্ষেত্রে ভুল করে পজিটিভ আসার প্রোবাবিলিটি কত? এই দ্বিতীয় সংখ্যাটাই ওই ‘ফলস পজিটিভ রেট’ অর্থাৎ ০.১%, আর
৩) অসুখটা কত রেয়ার বা কতটা কমন? মানে সে কি খুব আনকমন একটা জেনেটিক ডিজ-অর্ডার (যা মাত্র ১% লোকের হয়), না কি হাঁচি-কাশি কিম্বা পেটের ব্যামো? ধরে নেওয়া যাক, অসুখ-টা ভয়ানক বিরল, হয় দশ হাজারে এক জনের – মানে P(অসুখ) = ১/১০,০০০ = ০.০০০১)---
তাকে অডস এর ভাষ্যে:
Pre-test P(X) = 0.0001
Pre-test Odds(X) = 0.0001
আমরা এটিকে বলব প্রি-টেস্ট অডস |
এর পর আমরা বেইসিয়ান থিওরেম ধরে যেটি করি, সেটি হল একটি Likelihood Ratio স্থির করা। সেটি করতে গেলে আমাদের যে কোন পরীক্ষার sensitivity আর Specificity এই দুটো ব্যাপার জানার প্রয়োজন হয়।
বেইসিয়ান স্ট্যাটিসটিকস অনুযায়ী,
Sensitivity = P(T+ | D+)
(এর অর্থ, অসুখ যদি হয়ে থাকে, তাহলে কত শতাংশ ক্ষেত্রে টেস্ট পজিটিভ হবে) | এক্ষেত্রে যেটি আপনি খুব সুন্দর করে বুঝিয়েছেন এই লিখে:
"১) সত্যিকারের অসুখ থাকলে পজিটিভ রেজাল্ট আসার প্রোবাবিলিটি কত, ধরে নেওয়া যাক টেস্ট-টি খুব-ই উন্নতমানের, এবং এই প্রোবাবিলিটি-টি একের কাছে, ধরলাম ৯৯% বা ০.৯৯।"
তো Sensitivity = 0.99
আপনি যেটিকে False Positive বলছেন,
"সুস্থ মানুষের ক্ষেত্রে ভুল করে পজিটিভ আসার প্রোবাবিলিটি কত? এই দ্বিতীয় সংখ্যাটাই ওই ‘ফলস পজিটিভ রেট’ অর্থাৎ ০.১%"
সেটা বেইসিয়ান ভাষ্যে
False Positive = P(T+ | D-)
(সুস্থ মানুষ = অসুখ নেই, কিন্তু টেসট পজিটিভ এলো) |
এক্ষেত্রে,
False Positive = 0.1% = 0.001
আমরা Specificity নামে আরো একটি ব্যাপার বিবেচনা করি এবং বলি যে:
False Positivity = (1 - Specificity)
এই দুটিকে মিলিয়ে আমরা Likelihood Ratio নামে একটি পরিমাপ দেখি,
Likelihood Ratio = Sensitivity / (1 - Specificity)
বা পক্ষান্তরে,
Likelihood Ratio = Sensitivity / False Positive Rate
তা এই লাইকলিহুড রেশিও যে টেস্টের যত বেশী হবে, সেই টেস্ট তত কার্যকরী। তার একটা নোমোগ্রাম অবধি পাওয়া যায়, এই দেখুন,
 আমাদের উদাহরণ অনুযায়ী,
আমাদের উদাহরণ অনুযায়ী, Likelihood Ratio = 0.99/0.001 = 990
মানে আপনার এই টেসট খুবই ভাল যাকে বলে (নোমোগ্রামের একেবারে উঁচুতলার লেভেলের টেসট, :-) )
এখন এই Likelihood Ratio ব্যবহার করে আমরা একটি Posterior Odds নির্ণয় করি,
Posterior Odds (X) = Pre-test Odds(X) * Likelihood Ratio
আমাদের
Pre-test Odds(X) = 0.0001
Likelihood Ratio = 990
Post-test Odds(X) = 0.099
দেখুন টেসটটি এতটাই "সংবেদনশীল" যে, যে অসুখটিকে প্রাথমিকভাবে মনে করা হচ্ছিল যে ১ শতাংশেরও কম হওয়ার সম্ভাবনা, শুধু টেসটটি পজিটিভ হবার গুণে সে সম্ভাবনা প্রায় ৯৯০ গুণ বৃদ্ধি পেল। এতে করে অসুখটি যে হয়ে থাকতে পারে, তার এবারের "সম্ভাবনা" (মানে প্রোবাবিলিটি অর্থে) দাঁড়াল,
Post test P(X) = 0.090
যেমন লিখেছেন, প্রায় ১০ শতাংশে |
মানে কোথায় ১ শতাংশেরও কম সম্ভাবনা বলে মনে করা হচ্ছিল, আর কোথায় টেসট করার পর তার কতটা সম্ভাবনা বেড়ে গেল।
কাজেই কোন টেসট করা হচ্ছে, তার Sensitivity আর False Positive Rate এই দুটো ব্যাপার চিকিৎসকদের কাছে সাংঘাতিক রকম গুরুত্বপূর্ণ, এবং এই জায়গাটিতে বেইসিয়ান চিন্তাভাবনার অত্যন্ত গুরুত্বপূর্ণ অবদান রয়েছে।
 Abhyu | 47.39.***.*** | ১৫ মে ২০২১ ১০:৪৬105997
Abhyu | 47.39.***.*** | ১৫ মে ২০২১ ১০:৪৬105997খুবই গুরুত্বপূর্ণ লেখা, অরিনদা।
আরেকটা জিনিস নিয়ে লেখা যেতে পারে। হেমোফিলিয়া রোগ। মামার আছে। এবার প্রথম ভাগনের সুস্থ হবার চান্স কত? বড় ভাগনে সুস্থ হলে ছোটো ভাগনেও সুস্থ হবে তার চান্স কীরকম। রীতিমতো ফ্যামিলি প্ল্যানিং করার অঙ্ক :)
 অরিন | 161.65.***.*** | ১৫ মে ২০২১ ১২:০৭106004
অরিন | 161.65.***.*** | ১৫ মে ২০২১ ১২:০৭106004:-), একদম! দারুণ আইডিয়া!
-
π | ১৫ মে ২০২১ ১৫:১০106016
অরিনদা, যদুবাবু সবাইকেই অনেক ধন্যবাদ।
কিছু প্রশ্ন আছে। অ-জেনেটিক কোন অসুখ ধরুন। ইনফেকশাস, ভেকটর বর্ন। অর্থাত যেখানে অঞ্চলভেদে অসুখের প্রিভালেন্স অনেক আলাদা হতে পারে, নানাবিধ কারণে।
এবার ধরা যাক এমন একটা অঞ্চলে এই রোগ নিয়ে কাজ শুরু করা হল, যেখানে আগে কখনো এই রোগ নির্ধারণ করাই হয়নি। কিন্তু অসুখটা যে ছিলনা বলা যায়না। যেকোন এক্সিস্টিং রিপোর্টে এই অসুখগুলো ০ কেস দেখাবে। এবারে ধরুন আমি টেস্ট করলাম, কিছু গ্রামে, কিছু রান্ডম স্যাম্পল নিয়ে আর পজিটিভ পেলাম। পজিটিভিটি রেট। এনিয়ে যদুবাবুর সঙ্গে অনেক কথা হচ্ছিল। এই রেট দিয়ে প্রিভালেন্স বের করা নিয়ে।
অরিনদা যেটা দিলেন, সেটায় ওই প্রি টেস্ট কীভাবে ক্যালকুলেট করা হবে?
আর এটাকে ওই অঞ্চলের জন্য রেয়ার না প্রিভালেন্ট, এটাই বা আগে থেকে কীভাবে কী বলব, ঠিক করব?
এছাড়াও, টেস্ট কিটগুলোয় ব্রশিওরে অনেক ক্ষেত্রেই সেন্সিটিভিটি স্পেসিফিসিটি মেনশনড নেই, কিছু পাব্লিকেশন রেফার করা। সেসব পেপারে একেকটায় একেক রেজাল্ট। যে ল্যাবে টেস্ট হচ্ছে, সেই ল্যাব এই টেস্ট করে থাকলে তো আইডিয়াল হত, কিন্তু সেতো প্র্যাক্টিকালি বহু ক্ষেত্রে সম্ভব নয়। এক্ষেত্রে কী করেন লোকজন?
-
অরিন | ১৫ মে ২০২১ ১৬:১৮106019
"ওই প্রি টেস্ট কীভাবে ক্যালকুলেট করা হবে? "
সেনসিটিভিটি, স্পেসিফিসিটি যে কোন টেসটের নিজস্ব প্রপার্টি, টেসটের স্বকীয় ধর্ম | টেসট কিট ভেদে, অঞ্চলভেদে বা জনসমাজভেদে এর কোন পরিবর্তন হয় না। কিটের ব্রোশিওরে না লেখা থাকলেও কোন টেসট করা হচ্ছে তার একটা সাধারণত ধারণা থাকে, লিটারেচার দেখে ঠিক করে নিতে হয়। সেসব কিছুই জানা না থাকলে আগে একটা পাইলট অন্তত করে নিতে হবে, যাদের নিশ্চিত করে অসুখ আছে, যাদের নিশ্চিত করে অসুখ নেই, সেই ধরণের মানুষের মধ্যে স্টাডি করে। তা না হলে তো সেই টেস্ট ব্যবহার করা যাবে না।
প্রি-টেস্ট প্রোবাবিলিটি যে ব্যাপারটা, এই ক্ষেত্রে একটু জটিল ঠিকই, তবে সেটা যিনি ডাকতার, বা যিনি গবেষণা করছেন, তাঁর নিজের অভিজ্ঞতা বা বিশ্বাসের ওপর ছেড়ে দিতে হয়, যে তিনি কতটা প্রোবাবিলিটি বা অডস মনে করেন, যার জন্য এর পোষাকী নাম "প্রায়র বিলিফ" (পূর্বতন বিশ্বাস বলতে পারো) | এটা নির্ণয় করার জন্য আগের গ্রহীত ডাটা ব্যবহার করা যেতেও পারে, নাও যেতে পারে, সেক্ষেত্রে চিকিৎসকের নিজের ধারণার ওপর নির্ভর করতে হয়।
এর অর্থ, একজন, ব্যক্তিগত রোগীর ক্ষেত্রে টেসট করে পরীক্ষার আগের ডাকতারের রোগ নির্ণয় নিয়ে যা "বিশ্বাস", পরীক্ষার ফলাফল আসার পরে ডাকতার সেই রোগীর ক্ষেত্রে সেই "বিশ্বাস" থেকে কতটা সরে যাবেন, সেটা Sensitivity Specificity এর ওপরে নির্ভর করে।
এখানে যেটা আরেকটু জটিল, সেটা হল PPV (positive predictive value), মানে কত শতাংশ ক্ষেত্রে টেসট পজিটিভ হলে অসুখ আছে? বেইসিয়ান নিয়ম অনুযায়ী আমরা লিখতে পারি
P(D+ | T+) = Positive Predictive Value
মানে টেসট পজিটিভ হয়েছে ধরে নিয়ে অসুখ কত শতাংশ |
একটু অঙ্ক কষে (এখানে আর দেখালাম না) দেখা যেতে পারে যে,
P(D+ | T+) = P(T+ | D+) * P(D+) / P(T+ | D+) * P(D+) + P(T+ | D-) * (1 - P(D+))
এখানে
P(D+ | T+) = Positive Predictive Value
P(T+ | D+) = Sensitivity
P(T+ | D-) = False Positive Rate
P(D+) = অসুখের Prevalence
এখানে যে কথাটা বিশেষ করে বলার, সেটা হল এই পজিটিভ প্রেডিকটিভ ভ্যালু (মানে কত শতাংশ কেসে টেসট পজিটিভ হলে অসুখ আছে?) এটা কিন্তু নির্ভর করে কোন জনসমাজে বা কোথায় পরীক্ষা করা হচ্ছে, বা কি ধরণের অসুখ টেসট করা হচ্ছে।
খুব বিরল অসুখের ক্ষেত্রে (ধর ১০, ০০০ জনপ্রতি ১ জনের হয়, ক্যানসার ধরণের অসুখ), খুব ভাল টেসটের মানে খুব ভাল সেনসিটিভিটি স্পেসিফিসিটি আছে এমন টেসট, এক্ষেত্রেও পজিটিভ প্রেডিকটিভ ভ্যালু খুব কম হবে, মানে সে টেসট কোন কাজের হবে না, যদিও তার sensitivity specificity খুবই উঁচু দরের।
-
π | ১৫ মে ২০২১ ১৬:৩৯106022
ধব্যবাদ। তবে আমি কিটের সেন্সিসিটিভিটি স্পেসিফিসিটি অঞ্চল ভেদে আলাদা হুওয়ার কথা বলিনি। বিভিন্ন ল্যাবের কিট ইভ্যালুয়েশন রিপোর্টের পেপারগুলোতে আলাদা আলাদা ভ্যালু থাকার কথা বলেছি।
অঞ্চলের কথাটা পুরোটাই প্রিভালেন্স প্রসংগে আনা।
-
π | ১৫ মে ২০২১ ১৬:৪১106023
এই অঞ্চলে আগে জন্মেও যদি এইসব টেস্ট না হয়ে থাকে, তাহলে প্রায়োর বিলিফ কী ধরব?
-
যদুবাবু | ১৫ মে ২০২১ ২০:৪৩106033
@অরিন-দা, দারুণ, দারুণ ... ঐ নোমোগ্রামটা তো বিশেষ করে খুব ভালো লাগলো। এটা রেখে দিলাম সেভ করে। বাচ্চাদের দেখাবো এই জিনিষটা। এখন তো খালি অডস-এর ফর্মুলা দেখে।
আমি লেখার মাঝে একবার অডস দেবো কি দেবো না ভেবেছিলাম, তারপর না দেওয়াই ঠিক করলাম। আমার মনে হয়েছে, যেটা ভুল হতেই পারে, এই দেশের (মানে আম্রিকার) বাচ্চারা অডস খুব সহজে বোঝে, আমি ছোটোবেলায় ঠিক বুঝতাম না কেন জানিনা, প্রোবাবিলিটি-টা [০,১] বলে সুবিধে হতো। একেবারেই পার্সোন্যাল বায়াস। মানে ধরো আমার কলেজে পড়ার সময়েও "অডস" কাকে বলে জানতাম, কিন্তু অডস-এর টার্মস-এ ভাবতে শিখিনি, এখন যেমন পারি।
পরের পার্ট-টাও খুব কাজের। বিশেষ করে PPV ইত্যাদির সংজ্ঞা।
@π দি-র প্রশ্ন-টার একটা আমার-ও (১৬ঃ৪১)।
আমার মনে হয় একেবারে সেই নন-ইনফরমেটিভ প্রায়োর ধরে নিয়ে বেইজিয়ান করে পস্টেরিওর স্যামপ্লিং ইত্যাদি তো করাই যায় ... কিন্তু সে তো মহা ঝাম। এমনিতে কি করে?
@ অভ্যুদা- হ্যাঁ, ঐটা একটা অদ্ভুত ইণ্টারেস্টিং জিনিষ। Habsburg jaw নিয়ে অন্য একটা লেখায় একটু লিখেছিলাম, ইউরোপিয়ান রয়ালটিদের মধ্যে তো মারাত্মক।
 অরিন | 161.65.***.*** | ১৬ মে ২০২১ ০১:২৮106059
অরিন | 161.65.***.*** | ১৬ মে ২০২১ ০১:২৮106059পাই, "এই অঞ্চলে আগে জন্মেও যদি এইসব টেস্ট না হয়ে থাকে, তাহলে প্রায়োর বিলিফ কী ধরব? "
দেখ, কোন একটা আন্দাজর বশবর্তী হয়ে তো টেসটটি করা হচ্ছে? একদম অজানা অসুখেও সাইন সিমপটম দেখে কিছু টা আন্দাজ করা যায়। সেইটাকেই প্রায়র হিসেবে ধরতে হয়, কারণ এগুলো সব রিলেটিভ। অনেকে এ নিয়ে ডেলফি বা ধর একসপারটদের ওপিনিয়ন নেন। আর তা না হলে যদুবাবু যেমন প্রথম লেখাটায় লিখেছেন, যদি ঐ ধরণের অসুখ সম্বন্ধে কোন প্রিভালেনস ডাটা থাকে (ন্যাশনাল/ইনটারন্যালনাল), সেইটা ব্যবহার করতে হয়। অঞ্চলে অসুখ প্রথমবার হওয়া খুব স্বাভাবিক, তাতে ডায়গনস্টিক প্রপারটি বদলায় না, তবে PPV বিরল অসুখের ক্ষেত্রে খুব কম হবে।
শুধু খেয়াল রাখতে হবে যে টেসটের প্রপার্টি হচ্ছে sensitivity, specificity। ঐ জায়গাটায় কিছু করার নেই। কিটে লেখা থাকলে ভাল, না হলে একটা মেটা-অ্যানালিসিস দেখে নিলে কাজে দেবে।
- মতামত দিন
-
বিষয়বস্তু*:
-
গুরুচণ্ডা৯-র বই দত্তক নিন
কোনোরকম কর্পোরেট ফান্ডিং ছাড়া সম্পূর্ণরূপে জনতার শ্রম ও অর্থে পরিচালিত এই নন-প্রফিট এবং স্বাধীন উদ্যোগটিকে বাঁচিয়ে রাখতে এককালীন বা ধারাবাহিক ভাবে গুরুভার বহন করুন।
- ভাটিয়ালি | টইপত্তর | বুলবুলভাজা | হরিদাস পাল | খেরোর খাতা | বই
- টইপত্তর, ভাটিয়া৯, হরিদাস পাল(ব্লগ) এবং খেরোর খাতার লেখার বক্তব্য লেখকের নিজস্ব, গুরুচণ্ডা৯র কোন দায়িত্ব নেই। | ♦ : পঠিত সংখ্যাটি ১৩ই জানুয়ারি ২০২০ থেকে, লেখাটি যদি তার আগে লেখা হয়ে থাকে তাহলে এই সংখ্যাটি সঠিক পরিমাপ নয়। এই বিভ্রান্তির জন্য আমরা দুঃখিত।
















