- বুলবুলভাজা ভোটবাক্স লোকসভা - ২০২৪

-
ভক্স পপুলি
যদুবাবু
ভোটবাক্স | লোকসভা - ২০২৪ | ২৪ মে ২০২৪ | ২৫৮৭ বার পঠিত | রেটিং ৫ (৭ জন) - প্রথম কিস্তি | দ্বিতীয় কিস্তি | তৃতীয় কিস্তি | চতুর্থ কিস্তি | পঞ্চম কিস্তি | ষষ্ঠ কিস্তি | সপ্তম কিস্তি | অষ্টম কিস্তি | সমষ্টি থেকে ব্যষ্টি | ভক্স পপুলি | দুই লেজান্ড্রর গল্প | বিষের ইতিহাস, ইতিহাসের বিষ

“In general, a law which has not been voted unanimously involves subjecting men to an opinion which is not their own, or to a decision they believe contrary to their interest. It follows that a very great probability of the truth of this decision is the only reasonable and just grounds according to which one can demand such submission.”
- Marie-Jean-Antoine-Nicolas de Caritat, Marquis de Condorcet (September 17, 1743–March 28, 1794)
এই লেখাটা যখন লিখছি, অর্থাৎ এই ২০২৪-এর এপ্রিলের শেষ সপ্তাহে, আমাদের চারদিকে ভোটের দামামা বেজে গেছে। সামাজিক মাধ্যম থেকে শুরু করে সমস্তরকম খবরের চ্যানেল ভরে গেছে ভোট-সংক্রান্ত খবরে, হয় দলবদলের অলীক কুনাট্যরঙ্গ, না হলে অপদার্থ রাজনীতি-ব্যাবসায়ীদের তামাশা, অথবা কাদা-ছোঁড়াছুঁড়ির মহড়া। ভোট যত এগিয়ে আসবে, নিউজ়-ফিড ভরে যাবে বিচিত্র-বিবিধ সব “ফলিবেই ফলিবে” গোছের ভবিষ্যদ্বাণীতে, আর সেই নিয়ে নিত্যি তুফান উঠবে চায়ের কাপে আর আড্ডায়-তর্কে।
ভোটের ফলের পূর্বাভাস অথবা প্রেডিকশন কিন্তু সেই সমস্ত জটিল ধাঁধার মত—পরীক্ষায় যেসব প্রশ্নের উত্তর মাথা খাটিয়ে হোক কিংবা হল-কালেক্ট করে বা স্রেফ আন্দাজে ঢিল মেরে একবার মিলিয়ে দিতে পারেন, কেউ খুব বেশি মাথা ঘামাবে না ঠিক কেমন করে, কোন মেথডে মিলিয়েছেন। আমাদের ভাষায়, ইন্টারপ্রিটেবিলিটির (“কী করে?”) চাইতে অ্যাকিউরেসির (“কতটা মিলেছে”) দর ও কদর অনেক বেশি। আবার এও ঠিক, যে এই প্রতিযোগিতার পুরস্কার-তিরস্কার দুইই একটু বেশির দিকে। মিলিয়ে দিতে পারলে রাতারাতি সেলিব্রিটি, সবাই এসে থানে গড় করবে—যেমনটা হয়েছে বাবু নেট সিলভারের বেলায়—আর ফস্কে গেলে পাড়ার লোকে এসে বলে যাবে ‘সব ঢপ!’ সেই সঙ্গে, শুধু আপনার না, আপনার গোটা ফিল্ডের পাৎলুন ধরে টানামানি ব্যাপার।
সে যাই হোক, আপনাদের যদুবাবু সেফোলজিস্ট নন, রাজনৈতিক বিশেষজ্ঞ অর্থাৎ পোলিটিক্যাল পানডিট (পন্ডিত) – সেও নন। তবে নেট সিলভারের নামে ধন্যধন্য হয়েছিল যে বছর, যদুবাবুও সেই সময় কিঞ্চিৎ গৌরবে বহুবচ্চন হননি এ কথা বললে ডাহা মিথ্যে বলা হবে। তবে, আজ সে সব না। আজকে প্রেডিকশনের ধারকাছ দিয়েও যাবো না আমরা। বরং আমরা উত্তর খুঁজবো আরও গভীর, কিন্তু আপাতদৃষ্টিতে অতিসাধারণ একটি প্রশ্নের – গণতন্ত্র যে নির্বাচনের ভিত্তির উপর দাঁড়িয়ে, সেই জনমত কি সবসময়েই অভ্রান্ত? Is the vox populi always correct? সহজ করে বললে, একদল মানুষ অর্থাৎ ভোটদাতা কি সংখ্যাগরিষ্ঠতার মাধ্যমে সবসময়েই ঠিক সিদ্ধান্তে পৌঁছতে পারেন? আরেকভাবে বললে, যে মেজরিটি ভোটিং-এর উপর আমাদের গণতান্ত্রিক কাঠামোটিই দাঁড়িয়ে, সেই মেজরিটি কি সবসময়েই একটি অবজেক্টিভ (অর্থাৎ নৈর্ব্যক্তিক) সত্যতে পৌঁছুতে পারে? যদি পারে, তাহলে কখন পারে? আর যদি না পারে, তাহলে ঠিক কেমন ব্যাপার হয় সেটা? সামান্য এদিক-ওদিক দিয়ে কান ঘেঁষে না একেবারে বিচ্ছিরিভাবে ভুল? (এখানে ধরে নেওয়াই হচ্ছে যে একটি অবজেক্টিভ (অর্থাৎ বস্তুনিষ্ঠ বা নৈর্ব্যক্তিক) সত্যি আছে, অথবা, নির্বাচনের দিক থেকে ভাবলে সবার জন্যই (তর্কাতীতভাবে) মঙ্গলদায়ক এমন নীতি আছে।
এই যে সকলে মিলে ঠিক উত্তরে বা ঠিক সিদ্ধান্তে পৌঁছনোর ফেনোমেনন বা ঘটনা, এর-ই পোশাকি নাম “উইজ়ডম অফ ক্রাউড”, বাংলায় “সমষ্টিগত প্রজ্ঞা”। দর্শনে বা বিজ্ঞানের ইতিহাসে উইজ়ডম অফ ক্রাউডকে ব্যাখ্যা করার অথবা সংজ্ঞায় বা সূত্রে ধরার চেষ্টা বহুদিনের। আরও বহু জিনিসের মতোই, এর-ও সুতো ধরে টানতে টানতে পৌঁছে যাই সেই প্রাচীনকালের দার্শনিক অ্যারিস্টোটলের কাছে। ইনফর্মেশন এগ্রিগেশনের, বা তথ্য একত্র করার উপযোগিতার কথা সেই যুগে যারা ভাবতেন, তাঁদের মধ্যে সম্ভবত উনিই প্রথম। তবে, রাশিবিজ্ঞানের ছাত্রের কাছে “উইজ়ডম অফ ক্রাউডের” অতিপরিচিত গল্প অবশ্যই স্যার ফ্রান্সিস গ্যালটনের সেই বিখ্যাত এক্সপেরিমেন্ট, যেটি ছাপা হয়েছিল নেচার পত্রিকার মার্চ ১৯৪৯ সালের একটি নিবন্ধে, শিরোনাম “ভক্স পপুলি”। কীরকম ছিল সেই এক্সপেরিমেন্ট? গ্যালটন বর্ণনা দিয়েছেন প্লাইমাউথের একটি মেলার। সেখানে গেলে দেখা যেত একটি হৃষ্টপুষ্ট দুর্ভাগা ষাঁড় (ফ্যাটেনড অক্স) দাঁড়িয়ে আছে মেলার ঠিক মধ্যিখানে। দাঁড়িয়ে থাকার উদ্দেশ্য দর্শকদের মধ্যে একটি প্রতিযোগিতা – এই ষাঁড়টিকে কেটেকুটে পরিষ্কার করার পর সেই মাংসের ওজন কত হবে আন্দাজ করার। প্রতিযোগিতার প্রবেশমূল্য ধার্য করা হল ছয় পেনি, আর সবথেকে কাছাকাছি উত্তরের জন্য একটি পুরস্কার। গ্যালটন লিখছেন, ঐ ছয় পেনি মূল্যের উদ্দেশ্য—যাতে কেউ ইয়ার্কি মেরে ভুলভাল আন্দাজ না করেন (‘prevent from practical joking’), আর পুরস্কার পাওয়ার আশায় যারা আন্দাজ করছেন, তাঁরাও যথাসম্ভব সেরা আন্দাজ-ই করবেন (‘put the best bet’)। আর লিখেছেন, প্রতিযোগীদের বেশিরভাগ হয় চাষি, না হলে পশুপালক বা কসাই – কাজেই একেবারেই অন্ধকারে ঢিল ছোঁড়ার মত ব্যাপার নয়। ফল কী হল? গ্যালটনের পেপারে পাই, সেইদিনের ৮০০খানা উত্তরের মধ্যে ১৩টি অসম্পূর্ণ উত্তর বাদ দিয়ে যা পড়ে থাকে, তার মধ্যমা (মিডিয়ান) নিলে দাঁড়ায় ১২০৮ পাউন্ড, আসল ওজন—১১৯৭ পাউণ্ডের—এক শতাংশের মধ্যেই, আর গড় (অর্থাৎ মিন) নিলে উত্তর একেবারেই মিলে যাচ্ছে খাপে-খাপ, যাকে বলে নিখুঁত লক্ষ্যভেদ [Wallis, 2014]। উপসংহারে গ্যালটন মন্তব্য করছেন, “This result is, I think, more creditable to the trustworthiness of a democratic judgment than might have been expected.” …
শুধু আন্দাজ-মেলানো বা খেলা নয়, সমষ্টিগত প্রজ্ঞার বিভিন্ন ও বিচিত্র উদাহরণ কিন্তু দেখা যায় আমাদের প্রায় সমস্ত উদ্যোগেই, যেখানেই সিদ্ধান্ত নেওয়া (ডিসিশন-মেকিং) আর কিঞ্চিৎ অনিশ্চয়তা (আনসার্টনটি) মিশে আছে এমন সব ক্ষেত্রেই। যদি সত্য ধ্রুবক হয়, আর সমস্ত ভ্রান্তি যদ্দৃচ্ছ, অর্থাৎ এক-একটি ভুল এক-একদিকে টানছে (অর্থাৎ এররগুলো র্যান্ডম, সিস্টেমিক নয়), তাহলে গড় নিলে সেই সব ভুলগুলি কাটাকুটি করে ফলাফলের খুঁতশূন্যতা বা অ্যাকিউরেসি বাড়তে বাধ্য। এই নিয়ে ব্যাপক আলোচনার জন্য পাঠকদের “The Wisdom of the Crowds” [Surowiecki, 2005] বইটি সুপারিশ করে যাই।
কিন্তু আজকের গল্প আরও পুরোনো – এরও প্রায় দেড়শো বছর আগের ফ্রান্স যার পটভূমি। ইতিহাস বলে উইজ়ডম অফ ক্রাউডের প্রথম যথাযথ অঙ্কের সূত্র এসেছিল সেই ‘এজ অফ এনলাইটেনমেন্টের’ সময়, ফরাসি বিপ্লবের ঢেউ আছড়ে পড়ার অব্যবহিত আগে। সেই গল্পের নায়ক কনডরসে, পুরো নাম Marie Jean Antoine Nicolas de Caritat, Marquis de Condorcet! কনডরসে-কে বলা হয় “দি লাস্ট অফ দ্য ফিলোজ়ফস”, সেই “আলোকিত যুগের শেষ সাক্ষী” – ফরাসী বিপ্লবের ইতিহাসের একজন অতিমানবিক এবং অবশ্যই ট্র্যাজিক হিরো। তার গপ্পো করতে গেলে গোটা একটা বই-ই লিখে ফেলা যায়, তবু ছোট্ট করে বলি। কনডরসে মানবাধিকার ও সাম্যবাদে বিশ্বাস করতেন – সাম্যবাদ শুধু সব বর্ণের মধ্যেই নয়, সমস্ত অর্থনৈতিক শ্রেণির, এবং পুরুষ ও নারীর মধ্যেও। স্বল্প জীবনকালেই তিনি ওকালতি করেছিলেন শিক্ষাগত সংস্কার, প্রতিনিধিত্বমূলক সরকার, ঔপনিবেশিক দাসত্বের বিলুপ্তি এবং নারীর সমানাধিকার, বিশেষ করে সব জাতির সমতার জন্য এবং নারীদের ভোটাধিকার (উইমেন্স’ সাফ্রেজ) প্রশ্নের। এবং এই শেষতম প্রশ্নে, কনডরসে সেই আলোকিত যুগেও যেন উজ্জ্বল ব্যতিক্রম [Landes, 2009]। শেষ জীবনে, সেই কুখ্যাত রেইন অফ টেররের রোবস্পিয়েরের ভয়ে আত্মগোপন করা অবস্থাতেও তিনি লিখে চলেছেন তার সেরা কাজ Esquisse — লিখছেন সমাজের অগ্রগতির (“উন্নয়ন” বা “বিকাশ” আজকাল ব্যাঙ্গাত্মক শোনায়) কাঠামো, যার মূল স্তম্ভ মানুষের অসীম পরিপূর্ণতা (indefinite perfectibility of humankind and society)। কনডরসে-র আরও এক অন্যতম অবদান, “সোশ্যাল অ্যারিথমেটিক” – আজকে দাঁড়িয়ে মনে হয় সমাজের বিভিন্ন জটিল সমস্যায়, আর্থিক পরিকল্পনা থেকে জুরি-র সিদ্ধান্ত গ্রহণ, অথবা জনস্বাস্থ্য, সর্বব্যাপী রাশিবিজ্ঞান বা সম্ভাব্যতা-তত্ত্বের প্রয়োগের এক্কেবারে শুরুর দিকে চিন্তক ও দার্শনিক উনিই।
উইজ়ডম অফ ক্রাউডের গল্পে ফিরে আসি আবার। গ্যালটনের ১৬৪ বছর আগে, এই কনডরসে-ই, প্রথম অঙ্কের সূত্রে বেঁধেছিলেন সংখ্যাগরিষ্ঠের ব্যবহার – সমষ্টিগত প্রজ্ঞা অথবা মূর্খামি, দুইই। সেই বিখ্যাত উপপাদ্যটিই আজকে পরিচিত কনডরসে জুরি থিওরেম নামে, সংক্ষেপে CJT [Condorcet, 1785]। সেই উপপাদ্যটিই এখানে ছোট্ট করে, এবং সহজতম ভার্সনটিই, লেখার চেষ্টা করি। এই নিয়েও অবশ্য আস্ত বই আছে - Goodin and Spiekermann [2018], যদি পাঠকদের কারুর বিশদে পড়তে ইচ্ছে করে।
আবারও, ধরে নেওয়া যাক একটি অবজেক্টিভ অর্থাৎ বস্তুনিষ্ঠ সত্যি বা সেরা বিকল্প আছে, সেটা কী—না জানলেও চলবে, কিন্তু সে আছে, সেইটির জন্যেই ভোটাভুটি হচ্ছে। আর ধরা যাক আমাদের n-সংখ্যক ভোটার আছে, n বিজোড় সংখ্যা (অর্থাৎ “টাই” অসম্ভব)। প্রত্যেক ভোটারের ঠিক বিকল্পে ভোট দেওয়ার সম্ভাবনা ধরা যাক pc, এবং সবার ভোট পড়ে গেলে সিদ্ধান্ত নেওয়া হবে “মেজরিটি রুল” অনুযায়ী, অর্থাৎ যে সবথেকে বেশি ভোট পাবেন, সেটিই আমাদের গণতান্ত্রিক সিদ্ধান্ত। কনডরসে-র উপপাদ্যে এও ধরে নেওয়া হয়, যে, প্রত্যেক ভোটার ‘স্বতন্ত্র’, ‘দক্ষ’ এবং ‘আন্তরিক’। ‘স্বতন্ত্র’ – অর্থাৎ যে যার নিজের ভোট দিচ্ছেন বা একজনের পছন্দ আরেকজনকে প্রভাবিত করে না। ‘দক্ষ’ – অর্থাৎ, প্রত্যেকের ঠিক বিকল্প খুঁজে নেওয়ার সম্ভাবনা অর্ধেকের থেকে বেশি, যত সামান্যই হোক, এক্কেবারে র্যান্ডম গ্যেস অর্থাৎ ইকির-মিকির-চামচিকির করে আন্দাজে যা-ইচ্ছে-তাই একটা বোতাম টিপে দেওয়ার থেকে তার প্রজ্ঞা বা দক্ষতা একচুল হলেও বেশি। আর শেষ অ্যাজ়াম্পশনের কথা আগেও লিখেছি, ভোটার-রা ‘আন্তরিক’, সিরিয়াস-ও বলা যায়—কেউ ইচ্ছে করে ভুলভাল ভোট দিয়ে নষ্ট করছেন না।
কনডরসে-র উপপাদ্য বলে, এই সমস্ত অ্যাজ়াম্পশন সত্যি হলে, দুটো জিনিস হবেই – প্রথমত, মেজরিটি ভোটিং-এর মাধ্যমে ঠিক বিকল্প খুঁজে নেওয়ার সম্ভাব্যতা যেকোনো একজন ভোটারের ঐ এক-ই সম্ভাব্যতার থেকে বেশি হবে, আর যত ভোটারের সংখ্যা বাড়বে, ততই ঐ ঠিক উত্তরে পৌঁছনোর সম্ভাব্যতা ১-এর কাছাকাছি (অর্থাৎ ১০০%-এর কাছাকাছি) পৌঁছবে। সোজা বাংলায়, প্রচুর প্রচুর লোকে ভোট দিলে একেবারে ঠিক উত্তরে বা সেরা বিকল্পে পৌঁছনোর গ্যারান্টি দিচ্ছে CJT!
অঙ্কের ফর্মুলা এই নিবন্ধে না দিলেও চলে, এবং ইচ্ছে করলেই এই সূত্রটি সোজা টপকে পরের প্যারায় লাফিয়ে চলে যেতেই পারেন, তবে এত সুন্দর ফর্মুলা, যে না দিয়ে থাকতে পারছি না। CJT বলছে, যদি মেজরিটি ভোটিং-এর সিদ্ধান্ত “ঠিক” হওয়ার সম্ভাব্যতা হয় Pn আর এক-একজন ভোটারের “ঠিক” ভোট দেওয়ার সম্ভাব্যতা হয় pc, তাহলে অল্প অঙ্ক করলেই যে সূত্রটি পাওয়া যায় সেটা এইরকম: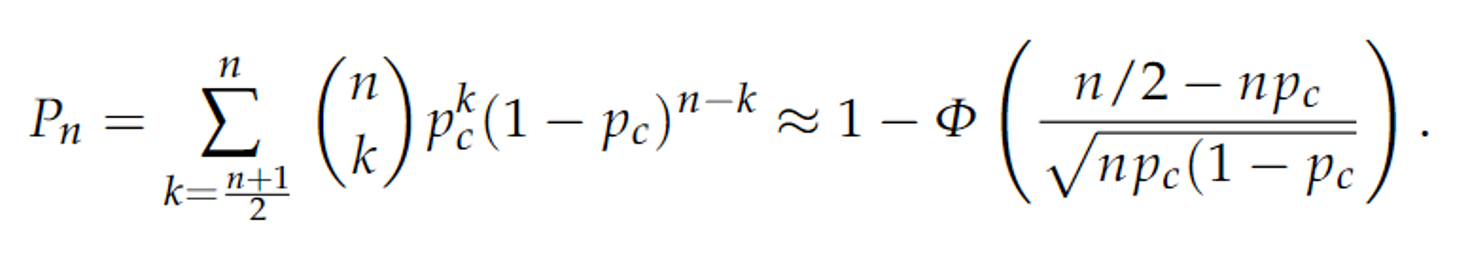
অর্থাৎ, CJT বলছে pc >1/2 হলে, অর্থাৎ দক্ষ ভোটার হলেই,
১) Pn+2 > Pn (মানে একজনের থেকে তিনজনের গড় নিলে ঠিক উত্তরে পৌঁছনোর সম্ভাবনা বেশি) আর
২) Pn → 1 as n → ∞ (মানে যত বেশি দক্ষ ভোটার ভোট দেবেন, তত ১-এর দিকে ক্রমাগত এগিয়ে যাব, নিচের ছবির উপরের ভাগে যেমন দেখা যাচ্ছে।)
বলাই বাহুল্য, যে এইটি একটু থেঁতো করে লেখা। এই উপপাদ্য একটু এদিক-ওদিক করলেও টেঁকে, যেমন সবার ঠিক উত্তর দেওয়ার সম্ভাবনা সমান নয়, না হলেও চলে, প্রত্যেকের সম্ভাবনা “আধা সে জ্যায়াদা” হলেই কেল্লা ফতেহ। আরো কিছু খোল ও নলচে পাল্টানো যায়, তবে কিনা, সে রাস্তায় আমরা আজকে যাবো না।
এই আশ্চর্য সুন্দর অথচ সহজ আবিষ্কারটি কিন্তু বহুদিন হারিয়ে গেছিল ইতিহাসের গর্ভে। তাকে খুঁজে পাওয়া যায় দীর্ঘ সময় পরে, ডানকান ব্ল্যাক ও অন্যান্যদের ১৯৫৮ সালের একটি গবেষণাপত্রে। শুধু জুরি থিওরেম-ই নয়, কনডরসে-র বিখ্যাত ভোটিং প্যারাডক্সটিও। সেটা আবার আরেক আশ্চর্য জিনিস – ধরা যাক তিনটে পার্টি আছে, ক, খ আর গ। তাহলে, মেজরিটি ভোটিং-এর ফলে এমন হতেই পারে, যে মানুষ ক-র থেকে বেশি পছন্দ করে খ-কে, আবার খয়ের থেকে বেশি গ-কে, অর্থাৎ গ > খ, এবং খ > ক, কিন্তু অঙ্কের মত এর মানেই গ > ক ভোট পাবে তার গ্রান্টি নেই, সবাই ভোট দেওয়ার পর হয়তো দেখা গেল ক, গ-কে হারিয়ে দিয়েছে। খটোমটো করে বললে, ব্যক্তিবিশেষের পছন্দ চক্রাকার নয়।
এই যেমন নিচের টেবিলটি দেখুন, আপনি যদি বলেন “গ”-ই সেরা, তক্ষুণি রাম আর শ্যাম বলবে – কেন, আমরা তো “গ”-এর থেকে “খ”-কে বেশি ভালোবাসি। আবার যেই বললেন – ঠিক আছে, তাহলে “খ”-কে জয়ী ঘোষণা করে দাও, তখন রাম আর মধু বলবে – সে কী! আমাদের চোখে তো “ক” অবশ্যই “খ”-এর থেকে ভালো। তাহলে কি “ক”-ই প্রধান-সেবক? নাঃ, শ্যাম আর মধু বলছে তাদের চোখে “গ”>”ক”! এ তো মহা মুশকিল!
(উপরের টেবিলে যদু কেন মিসিং সে প্রশ্ন প্লিজ করবেন না।)
এই ধাঁধার জট ছাড়াতেও আরেকটা গোটা লেখা দরকার, তবে কিনা, এই ছোট্ট ধাঁধার মধ্যেই লুকিয়ে আছে নোবেলজয়ী অ্যারো’জ় ইম্পসিবিলিটি থিওরেমের মূল সুর। যার মোদ্দা কথা – যে একদম সুষ্ঠুতম (ফেয়ারেস্ট) ভোটাভুটি হলেও এতোল-বেতোল লোকে জিতে যেতে পারে, মানে যাকে বলে ডেমোক্রেসির ফুটুরে একাধিক ডুমাডুম, অবশ্যই কিছু কিছু শর্ত সাপেক্ষে।
আবার লাইনে ফিরে আসি। এই যে উইজ়ডম অফ ক্রাউডের গপ্পো করে যাচ্ছি, এর প্রভাব বলুন বা প্রয়োগ – তা কিন্তু শুদ্ধু ভোটাভুটির ফলেই নয়, আরও অজস্র সহস্রবিধ চরিতার্থতায়। যেমন, আমাদের এই মেশিন লার্নিং-এর লাইনের আনসাম্বল লার্নার, উদাহরণ র্যান্ডম ফরেস্ট, যার আসল কথা এই, যে অনেকগুলো মডেলের প্রেডিকশন নিয়ে গড় করলে অ্যাকিউরেসি হু-হু করে বেড়ে যায়, যদি সেই মডেলগুলোর প্রত্যেকে মোটামুটি কিছুটা স্বতন্ত্র (“কিছুটা” মানে আমাদের লবজ়ে একেবারে ইন্ডিপেন্ডেন্ট না হলেও ডি-কোরিলেটেড, হুবহু টুকলি নয়), আর ‘দক্ষ’ হয় (প্রত্যেকেটা মডেল-ই আন্দাজে ঢিল মারার থেকে ভালো।)
আরো একটা অঙ্কের ফর্মুলা দিয়ে যাই, এ-ও স্বচ্ছন্দে রাস্তায় জমে থাকা জলের মত ডিঙিয়ে যেতে পারেন, ক্ষতি নেই। এটা রোমান ভার্শিনিনের বইয়ের অঙ্ক। (রাশিবিজ্ঞানের ছাত্র হলে প্রমাণ করার চেষ্টা করতেই পারো, দুই লাইনের প্রুফ।)
Consider a randomized algorithm for decision-making (e.g., determining if a number is prime) that gives correct answers with probability 1/2 + δ, where δ > 0 (i.e., assuming ‘competence’). By running the algorithm n times and taking the majority vote, the probability of obtaining the correct answer would be at least 1 − ε for any ε > 0, as long as,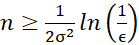
এ তো গেল সব ভালো ভালো কথা, “আমরা চলব আপন মতে, শেষে মিলব তাঁরি পথে” বলে কোরাসে গান গাওয়ার মত জায়গায় পৌঁছে গেছি প্রায়। কিন্তু তাহলে এই যে চাদ্দিকে বিভিন্ন সব অদ্ভুত ঘটনা দেখি – এই যেমন ব্রেক্সিট দেখলাম, ট্রাম্প-ও দেখলাম, আর আমাগো দ্যাশে তো আর কথাই নেই। এরা তো মেজরিটির-ই পছন্দ, তাহলে কোথায় গেলো সেই উইজ়ডম? এই যদি সেই বেড়াল, তবে মাংস কই? আর এই যদি সেই মাংস, তবে বেড়াল কই? তাহলে কি ঐ কনডরসে-র জুরি থিওরেম বাস্তব জগতে আর খাটে না?
এবার তাহলে আরেকবার ঝালিয়ে নেওয়া যাক কনডরসে-র উপপাদ্যের অ্যাজাম্পশনগুলো। ভোটার-দের হতে হবে “স্বতন্ত্র”, “দক্ষ”, এবং “আন্তরিক”। এর সবকটিই বিভিন্ন গবেষকের, বিভিন্ন মহলের প্রশ্নের মুখে পড়েছে বারংবার, যাদের কেউ-কেউ সত্যিই মনে করেন, যে এগুলো একসাথে সত্যি হওয়া প্রায় সোনার পাথরবাটির মত ব্যাপার।
এই যেমন ধরুন “দক্ষতা”! যদি সত্যিই এমন হয়, যে বেশির ভাগ লোকের-ই পছন্দ ভুল বিকল্পটিকে, অর্থাৎ অঙ্কের ফর্মুলায় ঐ pc < 1/2 হয়ে যায়? উপরের ছবিটির নিচের অর্ধেক দেখুন এইবার। হুহু করে কেমন গ্রাফ শূন্যের দিকে ছুটছে? অস্যার্থ, “ইনডিভিজুয়াল কম্পিটেন্স” অর্ধেকের কম হলে যত ভোটার বাড়বে তত বিপর্যয়, তত ভুল দিকে যাওয়ার রাস্তা মসৃণতর, সেইরকম কেসে শ্রেষ্ঠ জুরির সাইজ় মাত্র ১!
আর, “স্বাতন্ত্র্য”? ঐটিকে পলিটিক্যাল সায়েন্টিস্ট ও অন্যান্য সমাজবিজ্ঞানীরা আক্রমণ করেছেন মুহুর্মুহু। তাদের বক্তব্য, যদি সবার-ই এক-ই দিকে ‘সিস্টেম্যাটিক বায়াস’ থাকে, অথবা সবার কানে এক-ই প্রোপাগান্ডা পৌঁছয়? অথবা, সব ভোটারের খবরের সবটুকু অধিকার করে নেয় এক-ই উৎস থেকে আসা ফেক নিউজ বা মিসইনফর্মেশন? যদি সব্বার মধ্যেই এক-ই দিকে ধাবমান পক্ষপাত, একদেশদর্শিতা, এক-ই অন্ধবিশ্বাস, কুসংস্কার? সংখ্যাগরিষ্ঠর মধ্যে বিষক্রিয়ার মতই যদি ছড়িয়ে পড়ে এক-ই বিদ্বেষ? তারা কি সকলে, প্রত্যেকে একা, না পুরোটাই কোনো একটা মতবাদের একটিই অঙ্গমাত্র? এ ভয় কনডরসে-রও ছিল, তিনি লিখেছিলেন গণতন্ত্রের রোগ এই, যে ‘masses suffer from great ignorance with many prejudices’! আজ থেকে আড়াইশো বছর পরেও সে কথা অশ্লীল রকমের সত্যি বলে মনে হয়। তবুও, সেই ‘শেষ সত্য’ নয়!
আগেই লিখেছি, আবার-ও মনে করাই। কনডরসে-র জীবনের শ্রেষ্ঠ কাজ Esquisse যখন লিখছেন, তখন তিনি শাসকের চোখে দেশদ্রোহী। আত্মগোপন করে আছেন পরিবারের থেকে বহু দূরে কোথাও, মাথার উপর সাক্ষাৎ গিলোটিন। ভেবে আশ্চর্য লাগে, যে সেই অকল্পনীয় অবস্থায় নিশ্চিত মৃত্যুর অপেক্ষায় বসেও তিনি বলে যাচ্ছেন মানব সভ্যতার সামনে একটিই রাস্তা, সে রাস্তায় সাময়িক বাধাবিঘ্ন থাকলেও রাস্তাটার মুখ সোজা উপরের দিকে, যার শেষে আল্টিমেট পারফেকশন, অন্তিম পূর্ণতা, সে যেন এক ‘অন্তহীন নক্ষত্রের আলো’। এবং সেই শেষ সোপানে পৌঁছলে দেখা যাবে সেই বিশ্বে কোনো অসাম্য নেই, দেশে-দেশে, জাতিতে-জাতিতে মারামারি নেই, কারণ সেই সব-ই তো আসলে সভ্যতার প্রগতির পরিপন্থী! এই আকালেও তাই, আমার বিশ্বাস করতে ইচ্ছে হয়, ‘এই পথে আলো জ্বেলে—এ-পথেই পৃথিবীর ক্রমমুক্তি হবে’।
১৭৯৪ সালের ২৯শে মার্চ, ঠিক আজ থেকে ২৩০ বছর আগে, কনডরসের মৃত্যু হয় কারারুদ্ধ অবস্থায়, মৃত্যুর কারণ আজও অজানা, কেউ বলেন আত্মহত্যা, কেউ রাজনৈতিক খুন।
এই লেখাটার আর কোথাও যাওয়ার নেই আপাতত, অতএব এখানেই ইতি টানছি। শেষ করবো কনডরসে-র একটি অসামান্য উক্তি দিয়ে, এই লেখকের ঘিঞ্জি আপিসের ঘিঞ্জি বোর্ডের এক কোণে যেটি জ্বলজ্বল করে অজস্র আঁকিবুকি আর ভুল থিওরেমের মাঝে। অন্ধকার ও ক্লান্ত রাত্রে নির্জন হাইওয়ে ধরে একলা বাড়ি ফেরার রাস্তায় বহুদূর দিগন্তের জনপদের টিমটিমে আলোর মত সে যেন আমাকে পথ দেখায়।
“The truth belongs to those who seek it, not to those who claim to own it.”
সূত্রঃ- Duncan Black et al. The theory of committees and elections. 1958.
- Marie Jean Antoine Nicolas De Marquis De Caritat Condorcet. Essai sur l’application de l’analyse `a la probabilit ́e des d ́ecisions rendues `a la pluralit ́e des voix. 1785.
- Francis Galton. Vox populi (1907) nature, n. 1949, vol. 75, pp. 450-451 (traduzione di romolo giovanni capuano©). Nature, 75:450–451, 1949.
- Robert E Goodin and Kai Spiekermann. An epistemic theory of democracy. Oxford University Press, 2018.
- Scott Hill and Renaud-Philippe Garner. Virtue signaling and the Condorcet jury theorem. Synthese, 199(5):14821–14841, 2021.
- Joan Landes. The history of feminism: Marie-jean-antoine-nicolas de caritat, marquis de condorcet. 2009.
- James Surowiecki. The wisdom of crowds. Anchor, 2005.
- Roman Vershynin. High-dimensional probability: An introduction with applications in data science, volume 47. Cambridge University Press, 2018.
- Kenneth F Wallis. Revisiting Francis Galton’s forecasting competition. Statistical Science, pages 420–424, 2014.
পুনঃপ্রকাশ সম্পর্কিত নীতিঃ এই লেখাটি ছাপা, ডিজিটাল, দৃশ্য, শ্রাব্য, বা অন্য যেকোনো মাধ্যমে আংশিক বা সম্পূর্ণ ভাবে প্রতিলিপিকরণ বা অন্যত্র প্রকাশের জন্য গুরুচণ্ডা৯র অনুমতি বাধ্যতামূলক।প্রথম কিস্তি | দ্বিতীয় কিস্তি | তৃতীয় কিস্তি | চতুর্থ কিস্তি | পঞ্চম কিস্তি | ষষ্ঠ কিস্তি | সপ্তম কিস্তি | অষ্টম কিস্তি | সমষ্টি থেকে ব্যষ্টি | ভক্স পপুলি | দুই লেজান্ড্রর গল্প | বিষের ইতিহাস, ইতিহাসের বিষ - আরও পড়ুনফলিবেই ফলিবে (২০২৬) - যদুবাবুআরও পড়ুনরাধিকা ও আর্শোলা - যদুবাবুআরও পড়ুনতাই যেন হয় - যদুবাবুআরও পড়ুনআলো ঘন হয়ে আসছে - যদুবাবুআরও পড়ুনমোদী এসেছেন মার্কিনে। গোদি মিডিয়ার বাইরে যে সভ্য জগৎ, তার মিডিয়া রিপোর্ট সঙ্কলন। - Partha Banerjeeআরও পড়ুনরাবণের প্রার্থনা - তাতিনআরও পড়ুনআইটির ভাইটি - কণিষ্কআরও পড়ুনমধুবাতা ঋতায়তে - শারদা মণ্ডলআরও পড়ুনদিন গোনার দিন ৭ - হীরেন সিংহরায়আরও পড়ুনতিরিশ দিন অথবা এক কোটি ষোল লক্ষ ঘন্টা: শিক্ষা-ব্যবস্থার এক ভয়ঙ্কর জটিল অঙ্ক - সীমান্ত গুহঠাকুরতাআরও পড়ুনমধুবাতা ঋতায়তে - শারদা মণ্ডল
- মতামত দিন
-
বিষয়বস্তু*:
-
সমরেশ মুখার্জী | ৩০ এপ্রিল ২০২৪ ১২:৩২531236
- বিষয়টি আপাতবোধ্য। আসলে কঠিন। যদুবাবুর বিষয় নির্বাচনই অমন। তার ওপর বুদ্ধিযুক্ত মন্তব্য করা সহজ নয়। তবে অর্বাচীনের সে দায় নেই। ঐ যাদের প্রতি Mark Twain বলেছিলেন - It's better to keep your mouth shut and appear stupid than open it and remove all doubts.
তাই সেই সন্দেহ নিরসনে ব্রতী না হয়ে বরং শুধু বলি কনডরসের উক্তিটি দাগ কাটলো - কারণ প্রায়শই অজান্তে আমি (বা আমরা অনেকেই হয়তো) এই ভুল করে ফেলি - “The truth belongs to those who seek it, not to those who claim to own it.”
যদুবাবুর লেখার বিষয় Wisdom of the crowd পড়ে তার সাথে সম্পর্কবিযুক্ত একটা ব্যাপারও মনে এলো। কিছু বিষয় একবার পড়ে না বুঝতে পারলে জমিয়ে রাখি কোনো প্রসঙ্গে পরে পড়বার জন্য। মোবাইলে তেমনই একটা নিবন্ধ এসেছিল - Jan 10, 2023. জনৈক Shane Snow লিখিত (জানিনা কে তিনি) - Intellectual Dishonesty.ঐ নিবন্ধে উনি বলতে চেয়েছেন - “Discourse and debate are more effective in both democracy and business when we learn to be honest with ourselves and curb the subtle behaviours that get in the way of trading real ideas.”
তো Wisdom of Crowd প্রসঙ্গে কনডরসে তাঁর উপপাদ্যে যে তিনটি নির্ধারক ভেবেছিলেন
‘স্বতন্ত্রতা’, ‘দক্ষতা’ এবং ‘আন্তরিকতা’ - তা আজকের দিনে কতটা সম্ভব কেজানে। AI জাঁকিয়ে বসার আগেই প্রবল misinformation এর বন্যায় স্বতন্ত্রতা টলমল। ব্যক্তির দক্ষতার জমিতে নিয়ত ঢুকছে পক্ষপাত (bias), সংস্কার (prejudice) ইত্যকার বেনোজল। বিনামূল্যে মাসে পাঁচ কিলো চাল বা লক্ষ্মীর ভাণ্ডারে আন্তরিকতা বিক্রিত। এইসব কারণে ব্যক্তির নিরপেক্ষতা বিকৃত। তো তেমন ভীড়ের বিচক্ষণতা কতটা যুক্তিযুক্ত কে জানে। এখন গণতান্ত্রিক নির্বাচন মানে জনতার একটিই অপশন - ক্রমান্বয়ে কয়েকটি চোর, চোরনী বা ডাকাতকে পালা করে গদিতে বসানো যাতে কারোরই মৌরসীপাট্টা না হয়ে যায়।
“মনেরে আজ কহ যে
ভালো মন্দ যাহাই আসুক
সত্যেরে লও সহজে।”
সে না হয় হোলো। ভালো মন্দ যাই জানলুম হজম করে ঠুস মেরে বসে রইলুম। কিন্তু যদি আসে সত্য প্রকাশের ক্ষণ? কজন পারবে তা ব্যক্ত করতে? আর তখনই বহু ঋদ্ধসত্তা আশ্রয় নেবে ঐ ছাতার তলায় - যার নাম Intellectual Dishonesty.
 dc | 2402:e280:2141:1e8:3155:d0bc:e0:***:*** | ৩০ এপ্রিল ২০২৪ ১৩:১৯531239
dc | 2402:e280:2141:1e8:3155:d0bc:e0:***:*** | ৩০ এপ্রিল ২০২৪ ১৩:১৯531239- এই থিওরেমের সম্বন্ধে একদমই জানতাম না। থিওরেম অফ লার্জ নাম্বারস পড়ার সময়ে হয়তো আবছা কোথাও একটা পড়েছিলাম যে ডেমোক্রেটিক ভোটিং সিস্টেম নিয়েও অংক আছে, কিন্তু সে আর পড়া হয়ে ওঠেনি। যদুবাবুকে অনেক অনেক ধন্যবাদ এরকম সুন্দর একটা লেখার জন্য। আরও ধন্যবাদ ইকুয়েশানটার জন্য - এই সব ইকুয়েশান দেখলেই মনে হয়না, বিউটি অফ ম্যাথামেটিক্স? আর একটা জায়গায় একটু খটকা লাগলো। কনডরসের প্রাথমিক অ্যাসাম্পশানের মধ্যে একটা ছিল ভোটারদের ইন্ডিপেনডেন্স। আমার মনে হয় এইটেই বোধায় অধিকতম ভায়োলেটেড অ্যাসাম্পসান হবে রিয়েল লাইফে, যেমন যদুবাবু ও লিখেছেন। বেশীর ভাগ সময়ে ভোটাররা একযোগে ভোট দেয়, মোটামুটি অনেকে মিলে সিদ্ধান্ত নেয় যে এই নির্বাচনে এই দল বা প্রার্থী আমাদের পছন্দ, তাই একেই ভোট দেবো (যাকে বলে কোন দলের পক্ষে ওয়েভ)। আর এর সবথেকে এক্সট্রিম কেস বোধায় হলো প্রতি ভোটে দল পাল্টে দেওয়া, সে ঐ দল যাকিছুই করে থাকুক না কেন। তবে কিনা, এরকম কেস স্টাডি বোধায় করা যায় যে একটা ভোটার স্যাম্পল এ একটা প্রোপোর্শান m এর ভোট দেওয়ার সম্ভাবনা স্ট্রংলি কোরিলেটেড হবে (ধরা যাক r > .8), আর 1 - m প্রোপোর্শান এর ভোট দেওয়ার সম্ভাবনা উইকলি কোরিলেটেড হবে (ধরা যাক r < .3). অর্থাত যদুবাবু যে গ্রাফটা এঁকেছেন, সেটায় আরেকটা প্যারামিটার যোগ করলাম, r, এবার এই প্যারামিটারের বিভিন্ন ভ্যালুতে Pn কিরকম বিহেভ করবে সেটা দেখা যেতে পারে। (হয়তো এরকম কাজ অলরেডি কেউ করেছেন, সেক্ষেত্রে সরি চাই)।আরেকটু ছোট্ট কথা যোগ করবো - "তাদের বক্তব্য, যদি সবার-ই এক-ই দিকে ‘সিস্টেম্যাটিক বায়াস’ থাকে, অথবা সবার কানে এক-ই প্রোপাগান্ডা পৌঁছয়" - আমার মনে হয় সব সময়েই যে ভোটাররা চাপিয়ে দেওয়া প্রোপাগান্ডায় প্রভাবিত হন তা নাও হতে পারে, অনেক সময়ে তাঁদের নিজেদেরও একটা কালেকটিভ ডিসিশান থাকে, উদাহরন কেরল, যেখানে প্রতি বার অবধারিতভাবে পার্টি পাল্টে দেওয়া হয় (দুয়েকবার ব্যতিক্রম হয়)।
-
Prativa Sarker | ৩০ এপ্রিল ২০২৪ ১৫:১৬531240
- কনডরসকে জানার আগেই আমার মতো তুচ্ছ মানুষের বিশ্বাস, মানব সভ্যতা ওয়ান ওয়ে ট্রাফিক, সামনে এগোনো ছাড়া তার আর গত্যন্তর নেই। তবে সেই অন্তহীন নক্ষত্রের আলো দেখা তার কপালে আছে কিনা জানা নেই, তার আগেই রাজনীতিজ্ঞদের কল্যাণে পরিবেশের রুদ্র মূর্তিতে আমরা স্রেফ ফুটে যাব। যদুবাবু, তোমার মতো মাস্টারমশাই পেলে আমি বিজ্ঞান নিয়ে পড়তুম, অঙ্ককে এত ভয় পেতুম না।
-
যদুবাবু | ৩০ এপ্রিল ২০২৪ ২০:১৪531244
- সবাইকেই অনেক অনেক ধন্যবাদ। আগেও হয়তো এটা বলেছি কিন্তু গুরু-র সবথেকে বড় পাওনা এই যে আপনাদের/তোমাদের মত লোকের কাছে এইসব লেখা পৌঁছয়, সুচিন্তিত মতামত পাওয়া যায়। পরের ভাবনার খোরাক পাওয়া যায়। যে লেখাটা লিখেছি সেটা শুধুই এইসব আলোচনাগুলির সূত্রপাত হিসেবে ভাবতে ভালো লাগে।
এক এক করে উত্তর দিই।@সমরেশবাবু, আপনি একেবারেই ঠিক জায়গায় আলো ফেলেছেন। ইন্টেলেকচুয়াল ডিজঅনেস্টি আমাদের সমাজের একটি এপিডেমিক। না হলে ভাবুন না, এই বিশাল বিশাল পরিমাণের চুরি-ডাকাতির এতো ব্যাপক সোশ্যাল অ্যাক্সেপ্টেন্স আসে কী করে? "ভিড়ের বিচক্ষণতা" কথাটা ভালো লাগলো। তবে, ঐ, কী জানেন তো, বহুব্যবহারে ক্লিশে হয়ে গেলেও আমিও মনে করি 'কিন্তু মানুষের প্রতি বিশ্বাস হারানো পাপ, সে বিশ্বাস শেষ পর্যন্ত রক্ষা করব।'। যিনি লিখেছিলেন, তিনি আমাদের চেয়ে দুনিয়াদারি কিছু কম বুঝতেন না, বিশ্বযুদ্ধও দেখেছেন, দেখেও তো এই কথা লিখেছেন। লিখেছিলেন, "মনুষ্যত্বের অন্তহীন প্রতিকারহীন পরাভবকে চরম বলে বিশ্বাস করাকে আমি অপমান মনে করি।"
@ডিসি, হ্যাঁ, ইনডিপেন্ডেন্স, অর্থাৎ স্বতন্ত্রতা-র অ্যাজাম্পশন-টাই সবথেকে বেশি লোকের আপত্তির জায়গা। কারণ, মানুষ অত্যন্ত বেশি রকমের কনফর্মিটি-তে বিশ্বাস করে। ভালো হোক বা খারাপ, তার একলা হয়ে যাওয়ার ভয় সাংঘাতিক।
ঐ ডিপেন্ডেন্সি (যাকে আমি ইনএভিটেবল, অবশ্যম্ভাবী মনে করি) এবং পার্সন-টু-পার্সন হেটেরোজেনিটি মডেল করা একটা ভালো কাজ, কিন্তু আবার খুব জেনারেল সলিউশন বা ফ্রেমওয়ার্ক লেখাও চাপের। কেমন স্ট্রাকচার ধরব? ব্লক ডিপেন্ডেন্স হলে কেমন ব্লক-সাইজ়? কিছু নেগেটিভ কোরিলেশন-ও থাকা উচিত, নয়? মানে ঐ m, r ইত্যাদির বিভিন্ন ভ্যালু বসিয়ে বসিয়ে দেখা যায়, কিন্তু সেখান থেকে একটা জেনারেল ছবি অব্দি নিয়ে আসা বেশ চাপের কাজ। কেউ কেউ কিছু করেছেন কিন্তু "ভালো" মানে দেখে তৃপ্তি হবে এরকম কাজ দেখি নি। ইচ্ছে আছে এই নিয়ে অল্প কাজ করার -- কিন্তু হাজ়ারোঁ খোয়াইশে অ্যাইসি ...
এর সঙ্গে আরেকটা প্রবলেম আছে, কিছুটা ট্যানজেনশিয়ালি রিলেটেড, ঐ প্রেডিকশন সম্পর্কে। ইউ-এসে (ভারতেও হয়), প্রত্যেক ভোটের আগে একগাদা এগজিট পোল বেসড প্রেডিকশন পাওয়া যায় মার্কেটে, কেউ কেউ (যেমন নেট সিলভার) সেইগুলোকে বিভিন্ন ওয়েটেড অ্যাভারেজ (ঐ আনসাম্বল) করে নিজের প্রেডিকশন বানান। কাজটা সহজ নয়। কাকে কত ওজন দেবেন সেটা বেশ কঠিন প্রবলেম। আরও বিভিন্ন ব্যাপার আছে, যেমন পোলগুলি এক-ই সময়ে নেওয়া হয় না, আবার এক-একটার স্যাম্পল সাইজ এক এক রকম। সেইগুলোর বেশির ভাগ কি ঠিকঠাক প্রেডিক্ট করে, ওরাও কি ইনডিপেন্ডেন্ট? তাছাড়া, এও কি কিছুটা ক্যাওটিক সিস্টেমের মতন নয়, যেখানে প্রেডিকশন নিজেই ফাইন্যাল রেজ়াল্টকে প্রভাবিত করে? কিন্তু এই প্রসঙ্গটা ইচ্ছে করেই মূল লেখায় এড়িয়ে গেছি।
প্রতিভাদিঃ তোমার মন্তব্যটা এতো ভালো লাগলো যে কী বলবো। ছবি তুলে রেখে দিলাম। পরে কখনো যদি মনে হয় ধুর লিখে কী হবা, এইটা দেখে নেবো।
হ্যাঁ, "মানব সভ্যতা ওয়ান ওয়ে ট্রাফিক, সামনে এগোনো ছাড়া তার আর গত্যন্তর নেই" ... আমরা অন্তিম মূল্য পেতে চাই, শুধু প্রেম না, আশাতেও। ফুটে তো একদিন যাবোই। তবুও কি মাটি পেলে প্রতিমা বানাবো না?
-
অমিতাভ চক্রবর্ত্তী | ৩০ এপ্রিল ২০২৪ ২০:৫৭531245
- কঠিন বিষয়ে সহজ করে লেখা সারাৎসার প্রবন্ধ, পাঠকদের সুচন্তিত মন্তব্য এবং তার পর আরো বিশদে লেখকের সম্প্রসারিত আলোচনা। এই মিথষ্ক্রিয়ার ফল আমার মত নাদান পাঠকের জন্য চমৎকার প্রাপ্তি। কিন্তু বেতো ঘোড়া কিছুতেই নড়তে চায় না। খালি মনে হয় - “স্বতন্ত্র”, “দক্ষ”, এবং “আন্তরিক”, এর একটাও কি কাঙ্খিত মানের কাছে কোনদিন পৌঁছবে যাতে করে মনে হতে পারে প্রাপ্তব্য ফলটি সোনার পাথরবাটি নয়! তবে, আর এমন কোন পথও জানা নেই যাতে অই প্রাপ্তব্যটি পাওয়া যেতে পারে। অতএব চলতে থাকা।
সত্য, তাকে পাওয়া ইত্যাদি নিয়ে কথা এলেই আমার মিরোস্লাভ হোলুবকে মনে পড়ে যায়।
-
যদুবাবু | ০১ মে ২০২৪ ০৩:২৩531265
- পুরোপুরি না পৌঁছলেও কিছুটা হলেও ঠিক উত্তরে কনভার্জ করবে, অমিতাভদা। যেমন দক্ষ মানে স্রেফ অর্ধেকের থেকে বেশি প্রোবাবিলিটি যে সে ঠিক উত্তরটা (বা কোনটা দেশের ও দশের জন্য বেশি ভালো) মনে মনে জানে। বাকি দুটোর মধ্যে আন্তরিক নিয়ে কম সন্দেহ কিন্তু সন্দেহ আছেই। স্বতন্ত্র নিয়ে সবারই কিছু খটকা। ডিসি বা সমরেশ বাবু যা বললেন। বাকি তো আশা নিয়ে ঘর করি। আর পুরোটাই flawed বা hopeless ধরে নিলে আর কিছুই করার থাকে না। আমি সেই অব্দি নিজেকে নিয়ে যেতে পারি নি।মিরোস্লাভ হোলুব তুমি অনুবাদ করেছিলে না? না স্মৃতিবিভ্রাট হচ্ছে?
 পলিটিশিয়ান | 2603:8001:b102:14fa:3ef7:c64f:f155:***:*** | ০১ মে ২০২৪ ০৩:৫৬531266
পলিটিশিয়ান | 2603:8001:b102:14fa:3ef7:c64f:f155:***:*** | ০১ মে ২০২৪ ০৩:৫৬531266- ইন্ডিপেন্ডেন্স আর দক্ষতার সম্পর্ক কেমন হবে ভাবছি। ধরুন একটা গ্রূপ কোন প্রচারে বিভ্রান্ত হয়ে একটা দিকে ভোট দেবে ঠিক করল। তখন কি তাদের দক্ষ বলা যাবে? মানে তাদের দক্ষতা তো অবজারভেবল হবে না।
-
অমিতাভ চক্রবর্ত্তী | ০১ মে ২০২৪ ০৪:০০531267
- সে ত বটেই, আশা নিয়ে থাকতে না পারলে থাকাই কঠিন। আমি সুযোগ পাই বা না পাই হোলুবের কথা পেড়ে বসি। ওনার লেখার রসগ্রহণ সম্ভব হয়েছিল মানবেন্দ্র বন্দ্যোপাধ্যায়ের অসামান্য অনুবাদে। পরে কিছু কবিতা ইংরেজিতে পড়েছি।
-
যদুবাবু | ০১ মে ২০২৪ ০৪:৩৪531268
- "বিভ্রান্ত" হলে আর দক্ষ বলা যাবে না মনে হয়। :) Goodin আর Spiekerman এর বইয়ের একটা epilogue আছে। পুরোটাই এই নিয়ে। তবে ওদের উদাহরণ বা কেস স্টাডি ট্রাম্প।
 dc | 2402:e280:2141:1e8:c10e:ce24:271c:***:*** | ০১ মে ২০২৪ ০৯:২০531270
dc | 2402:e280:2141:1e8:c10e:ce24:271c:***:*** | ০১ মে ২০২৪ ০৯:২০531270- যদুবাবু, উত্তরের জন্য ধন্যবাদ। হ্যাঁ, ঠিকমতো ওয়েটেজ বানানো ইটসেল্ফ একটা নন-ট্রিভিয়াল কাজ। হয়তো সিমুলেশান করে ওয়েটগুলোর ভ্যালু বার করা যায়, কিন্তু পোলিং এজেন্সিগুলো কি অতোদূর যায়? কি জানি! "এও কি কিছুটা ক্যাওটিক সিস্টেমের মতন নয়" - একদম! আর পলিটিকাল পার্টিগুলোও সেটা জানে, সেইজন্যই দেখুন হাজারটা প্রি পোল ফোরকাস্ট বার হচ্ছে, যাতে বিজেপি অলরেডি জিতে বসে আছে :-)"খালি মনে হয় - “স্বতন্ত্র”, “দক্ষ”, এবং “আন্তরিক”, এর একটাও কি কাঙ্খিত মানের কাছে কোনদিন পৌঁছবে যাতে করে মনে হতে পারে প্রাপ্তব্য ফলটি সোনার পাথরবাটি নয়!"অমিতাভদার এই মন্তব্যটা খুব মূল্যবান, যেকোন মডেলিং এর মূল কথা। যেকোন সিস্টেম মডেল করতে গেলে প্রথমে আমরা কিছু অ্যাসাম্পশান নিয়ে শুরু করি, সেগুলোর ভিত্তিতে একটা রেস্ট্রিকটেড মডেল বানাই। তারপর অ্যাসাম্পসানগুলো এক এক করে রিল্যাক্স করে দেখি মডেলটা কেমন বিহেভ করছে, রিল্যাক্স করলেও ঠিকমতো প্রেডিক্ট করছে কিনা। যদুবাবু যেমন বললেন, এক্ষেত্রে কনভার্জ করারই কথা। তার কারন আমার মনে হয় লুকিয়ে আছে ল অফ লার্জ নাম্বারের মধ্যে, অর্থাত স্যাম্পল সাইজ বাড়ানোর মধ্যে (যদুবাবুর গ্রাফে দেখুন, যতো ডানদিকে যাবেন ততো স্যাম্পল সাইজ বাড়বে, আর Pn এর মান ১ কে অ্যাসিম্পটোটিকালি অ্যাপ্রোচ করবে)।
-
অমিতাভ চক্রবর্ত্তী | ০১ মে ২০২৪ ১০:১৩531272
- ডিসি, “স্বতন্ত্র”, “দক্ষ”, এবং “আন্তরিক”, এর “স্বতন্ত্র” নিয়ে খটকা এবং “আন্তরিক” নিয়ে সংশয় এর কথা যদুবাবুর মতো তুমিও নিশ্চয় মানবে। নিঃসংশয় বাজির একটিই ঘোড়া "দক্ষ"। আশায় বাঁচা মানুষ এই ভরসায় থাকে যে ওটা যদি ৫০ শতাংশের একটু হলেও বেশি থাকে, তা হলেই কেল্লা ফতে। এইবার পপুলেশন যতো লার্জ হবে কাঙ্খিত ফল তত হাতের নাগালে আসবে। কিন্তু, কেল্লাদারও সেটা জানে। আর তাই সে তার সমস্ত মায়ার খেলা বিস্তৃত করে দক্ষতাকে বেশি না, স্রেফ ঐ ৫০ শতাংশের একটু হলেও নীচে নামিয়ে আনতে চেষ্টা চালিয়ে যাবে। এবার পপুলেশন যতো লার্জ হবে কাঙ্খিত ফল তত ভোটারের নাগালের বাইরে চলে যাবে। তা হলে আশার জায়গাটা কোথায়? পরিশ্রমের কোন বিকল্প নেই আর অনুশীলন কাজকে নিখুঁত করার দিকে এগিয়ে নিয়ে যায়। পপুলেশন ত লার্জ হয়েই আছে, আরো হবে।
 dc | 2402:e280:2141:1e8:c10e:ce24:271c:***:*** | ০১ মে ২০২৪ ১০:৩৩531273
dc | 2402:e280:2141:1e8:c10e:ce24:271c:***:*** | ০১ মে ২০২৪ ১০:৩৩531273- অমিতাভদা, একটু দ্বিমত আছে :-)এখানে "দক্ষ" কথাটার মানে হলো Pc > .5. যদুবাবুও লিখছেন দেখছি, "‘দক্ষ’ – অর্থাৎ, প্রত্যেকের ঠিক বিকল্প খুঁজে নেওয়ার সম্ভাবনা অর্ধেকের থেকে বেশি, যত সামান্যই হোক, এক্কেবারে র্যান্ডম গ্যেস অর্থাৎ ইকির-মিকির-চামচিকির করে আন্দাজে যা-ইচ্ছে-তাই একটা বোতাম টিপে দেওয়ার থেকে তার প্রজ্ঞা বা দক্ষতা একচুল হলেও বেশি।"আমি যেটুকু বুঝছি, এখানে "দক্ষ"তা একটা আ প্রায়োরি অ্যাসাম্পশান, অর্থাত এই থিওরেমের সাপেক্ষে দক্ষতাকে ম্যানিপুলেট করা যাবেনা। রিয়েল লাইফের কথা যদি বলেন, "দক্ষ" মানে বোধায়, একজন মানুষের বোঝার ক্ষমতা, কে সিস্টেমের জন্য ভালো আর কে খারাপ। আর সেখান থেকেই উইজডম অফ দ্য ক্রাউডের কথা আসছে, যে অনেকে মিলে ঠিক ডিসিশান নেওয়া যায় কিনা। তো পলিটিকাল পার্টিগুলোর উদ্দেশ্য বোধায় নিজেকে বেটার অলটারনেটিভ হিসেবে প্রোজেক্ট করা, যাতে ভোটার ঐ Pc > .5 নিয়ে তার দিকে ভোট দেয়। অর্থাত ভোটারের দক্ষতাকে ম্যানিপুলেট করা নয়, উদ্দেশ্য হলো নিজেকে বেটার অলটারনেটিভ হিসেবে প্রোজেক্ট করা। এটা আমার মনে হলো, আমি ভুল হতে পারি।
 dc | 2402:e280:2141:1e8:c10e:ce24:271c:***:*** | ০১ মে ২০২৪ ১০:৪০531274
dc | 2402:e280:2141:1e8:c10e:ce24:271c:***:*** | ০১ মে ২০২৪ ১০:৪০531274- আরেকটু পড়ে দেখলাম, ইংরেজি কথাটা বোধায় competence. কম্পিটেন্সের বাংলা কি দক্ষতা? এটাও ঠিক শিওর নই।
-
অমিতাভ চক্রবর্ত্তী | ০১ মে ২০২৪ ১১:১৩531276
- ডিসি, গুগ্লিয়ে দেখলাম
competence = কর্মদক্ষতা, যোগ্যতা, ক্ষমতা ইত্যাদি।
আমি মূল ইংরেজি লেখা পড়িনি। যদুবাবু যতটূকু শেখালেন সেটুকুই বুঝতে চেষ্টা করেছি। যদুবাবু বলেছেনঃ
"কনডরসে-র উপপাদ্যে এও ধরে নেওয়া হয়, যে, প্রত্যেক ভোটার ‘স্বতন্ত্র’, ‘দক্ষ’ এবং ‘আন্তরিক’। ‘স্বতন্ত্র’ – অর্থাৎ যে যার নিজের ভোট দিচ্ছেন বা একজনের পছন্দ আরেকজনকে প্রভাবিত করে না। ‘দক্ষ’ – অর্থাৎ, প্রত্যেকের ঠিক বিকল্প খুঁজে নেওয়ার সম্ভাবনা অর্ধেকের থেকে বেশি, যত সামান্যই হোক, এক্কেবারে র্যান্ডম গ্যেস অর্থাৎ ইকির-মিকির-চামচিকির করে আন্দাজে যা-ইচ্ছে-তাই একটা বোতাম টিপে দেওয়ার থেকে তার প্রজ্ঞা বা দক্ষতা একচুল হলেও বেশি। আর শেষ অ্যাজ়াম্পশনের কথা আগেও লিখেছি, ভোটার-রা ‘আন্তরিক’, সিরিয়াস-ও বলা যায়—কেউ ইচ্ছে করে ভুলভাল ভোট দিয়ে নষ্ট করছেন না।"
তাই দক্ষতা বলতে ভোটারের দক্ষতা বুঝেছি, তার প্রভাবকের মানে ভোটপ্রার্থীর competence বুঝিনি। এই, আর কিছু বলার নাই।
 অরিন | 119.224.***.*** | ০১ মে ২০২৪ ১১:৩৭531277
অরিন | 119.224.***.*** | ০১ মে ২০২৪ ১১:৩৭531277- যদুবাবু, অসাধারণ হয়েছে। পড়ে আনন্দ হল।আপনার, অমিতাভবাবুর আর dc র আলোচনা পড়তে পড়তে Bayesian Decision Theory'র সঙ্গে condorset jury theorem এর সম্পর্কের কথা মনে হচ্ছিল ।কনডরসে ছিলেন Laplace এর "গুরু", এবং Bayes এর কথা তাঁর বন্ধু রিচার্ড প্রাইস কনডরসেকে জানান। এ সব আপনার জানা, তবুও, তাও যদি সেই চেনাজানার ইতিহাস পড়তে ভাল লাগে, সেই ভেবে, লিঙ্কটা রাখলাম,অমিতাভ বাবু মিরোস্লাভ হোলুবের কবিতার গুণগ্রাহী জেনে ভারি ভাল লাগল।
-
অমিতাভ চক্রবর্ত্তী | ০১ মে ২০২৪ ১১:৫২531279
- অরিন হে, হোলুবের একাধিক কবিতা একসময় জোর করে লোকজনকে পড়ে শোনাতাম, সে তাদের তেমন ভালো লাগুক চাই না লাগুক। আমার বিবিধ পাগলামির এটাও একটা। এখন আমি ওসব করি না। শুধু হোলুবের নাম নিয়ে চুপ করে যাই। দেশ ছাড়ার সময় যে গুটিকয় বই নিয়ে এসেছিলাম, মানবেন্দ্র বন্দ্যোপাধ্যায়ের করা হোলুবের অনুবাদ তার একটি।

-
অরিন | ০১ মে ২০২৪ ১২:১৯531280
- এই টইটাকে মিরোস্লাভ হোলুবের কবিতা দিয়ে হাইজ্যাক করা উচিৎ নয়, :-), তাও casualty কবিতার লাইনগুলো না লিখে থাকতে পারলাম না,"... And while we are suturing
inch after inch,
night after night,
nerve to nerve,
muscle to muscle,
eyes to sight,
they bring in
even longer daggers,
even more dangerous bombs,
even more glorious victories,
idiots."আজকের দুনিয়ায় যে কি ঘোর বাস্তব, একজন চিকিৎসক হিসেবে রোজ খারাপ লাগে।
-
অমিতাভ চক্রবর্ত্তী | ০১ মে ২০২৪ ১২:২৪531281
- সেই।
-
পাপাঙ্গুল | ০১ মে ২০২৪ ১৩:০০531284

-
অমিতাভ চক্রবর্ত্তী | ০১ মে ২০২৪ ১৩:২১531285
- সেইইইইইইই বই
 মাস্টারমশাইয়ের লেখা পড়েছে একদল বইয়ের ভিতর অন্য বই পড়ার হাতে। ঠিক হচ্ছে না কিন্তু।
মাস্টারমশাইয়ের লেখা পড়েছে একদল বইয়ের ভিতর অন্য বই পড়ার হাতে। ঠিক হচ্ছে না কিন্তু।
-
Sara Man | ০১ মে ২০২৪ ২১:৩১531295
- যদুবাবুকে আরও অল্প বয়স থেকে টিউটর হিসেবে পেলে আমার খুব ভালো হত।
-
প্যালারাম | ০১ মে ২০২৪ ২২:৪২531296
- ঠিকহল না ,আবার হলও। কনডরসের সঙ্গে হোলুব ফ্রি পাওয়া গেল... লাভ (উভয়ার্থে)

-
যদুবাবু | ০১ মে ২০২৪ ২৩:৪২531299
- এই রে অনেকক্ষণ ঢুকিনি গুরুতে। আসলে আজ রাস্তায় এবং মাঝেমধ্যে উড্ডীন। হোলুবের কবিতা দিয়ে আমার সব টই হাইজ্যাক হলেও বিন্দুমাত্র দুঃখ নেই। অত্যন্ত প্রিয় কবি। আর কি বলি, এই বইটা আমারও ছিল। তারপর, ওই ... "লিখিও উহা ফিরৎ চাহো কিনা?" ফোঁত।অমিতাভদা, আবার লোককে ধরে পড়ে শোনাতে শুরু করো। আমি ন্যাশভিলে গেলে আমিই শুনে আসবো।:)ডিসি/অমিতাভ দা, হ্যাঁ দক্ষ লিখতে একটু খুঁত খুঁত করছিল, আবার "যোগ্য" লিখতে চাইনি। সত্যি বলতে competent ও ঠিক ঠিক ধরতে পারে না বলে মনে হয়েছিল। একজন মানুষ যিনি ঠিক দিকটিকে ভুল দিকের থেকে বেশি চেনেন, এর এক কথায় প্রকাশ করার মত শব্দ কি?অরিনদা (থুড়ি, লান), ঠিকই। Bayesian decision theory র ভিত বোধহয় ওই সময় থেকে একটু একটু করে তয়ের হচ্ছে।আর এই Laplace আরেক আশ্চর্য মানুষ। অতিমানবিক।এটা লিখতে লিখতে মনে পড়ল — ইচ্ছে আছে কখনও এই সোশ্যাল আরিথমেটিক কিভাবে ম্যাক্সওয়েলকে প্রভাবিত করেছিল Kinetic theory ভাবায় সেই বিষয়ে লিখবো। তবে খুবই সাহস করতে হবে আর কি। তাও একটা excerpt দি।The modern atomists," observed James Clerk Maxwell in 1873, "have... adopted a method which is, I believe, new in the departmentof mathematical physics, though it has long been in use in the section of statistics." The number of individuals in a census is far too great for statisticians to trace the history of each separately, "so that, in order to reduce their labour within human limits, they concentrate their attention on a small number of artificial groups" divided according to age, tax, education, religion, and so on. Similarly, the atomist lacks the perfect knowledge of all particles required for the application of the historical, or dynamical method to gas theory."অথচ, এই সুন্দর analogy টা কেউ কখনও অফিসিয়াল স্ট্যাট পড়াতে গিয়ে বলেন না।শারদা দি, অজস্র ধন্যবাদ। :) আমি পড়াতে খুব ভালবাসি। সেমিস্টার শেষ হলে একটু মন খারাপ হয়ে যায়।প্যালারামকে কিছু বলার নেই। তুমি আবার এই রদ্দি জিনিষ দু দুটো ভাষায় পড়েছ। তোমাকে ধৈর্য্যশ্রী উপাধি দেওয়া উচিত। :D
-
হীরেন সিংহরায় | ২৩ মে ২০২৪ ১৮:৫৩532236
- ১৯১৯ সালের ভাইমার সংবিধান যে নির্বাচন পদ্ধতি নির্দিষ্ট করে দেয় ( আজও জারমানি ছাড়া বহু দেশে চালু ) সেটি মনে হয় এক বাকসোর প্রতিফলন !
-
হীরেন সিংহরায় | ২৩ মে ২০২৪ ১৮:৫৫532237
- এই বাকসো বলতে চেয়েছিলাম এক বাকসো নয় । ব্যতিক্রম - তৃতীয় পছন্দের খাতির নেই! প্রথম ও দ্বিতীয় মাত্র
-
সমরেশ মুখার্জী | ২৩ মে ২০২৪ ২৩:২৬532252
- গুরুর গুগলি - ভক্স পপুলি
যদুবাবুর যে লেখাটি 30.4.24 টুকরো বুবুভায় পোষ্ট হয়েছিল - যাতে আমারই প্রথম মন্তব্য পড়েছিল - সেটাই দেখছি আজ 23.5 টুকরো বুবুভায় পুনঃপোষ্টিত হয়েছে 1055 ভিউ / 25 কমেন্টস সমেত। তাতে কোনো অসুবিধা নেই - কিন্তু পোষ্টিং ডেট দেখাচ্ছে 24.5 - মানে আগামীকাল !!গুরুর মায়াপাতায় কি সালতারিখও মায়াময়??
-
যদুবাবু | ২৪ মে ২০২৪ ০১:৫৩532262
- @ হীরেনদা, ভাইমার সংবিধান বিষয়ে খুব একটা জানি না। পড়ে দেখতে হবে। তবে, এই সোশ্যাল চয়েস থিয়োরি বহুচর্চিত অর্থনীতির বিষয়, খুবই ইন্টারেস্টিং। আমি খুব বেশি জানি না। আমাদের অমর্ত্য সেনের পেপার পড়েছিলাম অনেকদিন আগে, তার টাইটেল মনে আছে, How to judge voting schemes!Arrow's Impossibility Theorem আমার খুব প্রিয় বিষয় — তবে লেখার সাহস নেই এই মুহূর্তে।@ সমরেশবাবু, হ্যাঁ তাই দেখছি। সময় বলে আসলে কিছুই নেই। সাল তারিখ সেকেন্ড ঘণ্টা সবই মায়া। বোর্হেস বলেছিলেন, "with you and without you, are the only ways I know how to measure time." আমিও ওঁর দলে - ঐভাবেই দিনক্ষণ মাপি।যাহোক, লেখাটা কেউ তুলে এনেছেন বলে হীরেনদার মন্তব্য পেলাম। ভালো লাগলো। :)
 dc | 2402:e280:2141:1e8:bc0a:c7bb:df07:***:*** | ২৪ মে ২০২৪ ০৮:০৯532269
dc | 2402:e280:2141:1e8:bc0a:c7bb:df07:***:*** | ২৪ মে ২০২৪ ০৮:০৯532269- তাহলে এই গানটা থক, উইথ অর উইদাউট ইউ
- মতামত দিন
-
বিষয়বস্তু*:
-
গুরুচণ্ডা৯-র বই দত্তক নিন
কোনোরকম কর্পোরেট ফান্ডিং ছাড়া সম্পূর্ণরূপে জনতার শ্রম ও অর্থে পরিচালিত এই নন-প্রফিট এবং স্বাধীন উদ্যোগটিকে বাঁচিয়ে রাখতে এককালীন বা ধারাবাহিক ভাবে গুরুভার বহন করুন।
- ভাটিয়ালি | টইপত্তর | বুলবুলভাজা | হরিদাস পাল | খেরোর খাতা | বই
- বুলবুলভাজা : সর্বশেষ লেখাগুলি
(লিখছেন... Aditi Dasgupta, হীরেন সিংহরায়, Sara Man)
(লিখছেন... হীরেন সিংহরায়, শিবাংশু, রমিত চট্টোপাধ্যায়)
(লিখছেন... )
(লিখছেন... Srimallar, .)
(লিখছেন... Sara Man, Supriyo Mondal, Sara Man)
- হরিদাস পালেরা : যাঁরা সম্প্রতি লিখেছেন
(লিখছেন... :|:, bikarna, bikarna)
(লিখছেন... )
(লিখছেন... :|:, aranya, dc)
(লিখছেন... )
(লিখছেন... দ, হীরেন সিংহরায়, Tuhinangshu Mukherjee)
- টইপত্তর : সর্বশেষ লেখাগুলি
(লিখছেন... Srimallar)
(লিখছেন... Bratin Das)
(লিখছেন... সচ্চরিত্র, albert banerjee)
(লিখছেন... )
(লিখছেন... )
- কি, কেন, ইত্যাদি
- বাজার অর্থনীতির ধরাবাঁধা খাদ্য-খাদক সম্পর্কের বাইরে বেরিয়ে এসে এমন এক আস্তানা বানাব আমরা, যেখানে ক্রমশ: মুছে যাবে লেখক ও পাঠকের বিস্তীর্ণ ব্যবধান। পাঠকই লেখক হবে, মিডিয়ার জগতে থাকবেনা কোন ব্যকরণশিক্ষক, ক্লাসরুমে থাকবেনা মিডিয়ার মাস্টারমশাইয়ের জন্য কোন বিশেষ প্ল্যাটফর্ম। এসব আদৌ হবে কিনা, গুরুচণ্ডালি টিকবে কিনা, সে পরের কথা, কিন্তু দু পা ফেলে দেখতে দোষ কী? ... আরও ...
- আমাদের কথা
- আপনি কি কম্পিউটার স্যাভি? সারাদিন মেশিনের সামনে বসে থেকে আপনার ঘাড়ে পিঠে কি স্পন্ডেলাইটিস আর চোখে পুরু অ্যান্টিগ্লেয়ার হাইপাওয়ার চশমা? এন্টার মেরে মেরে ডান হাতের কড়ি আঙুলে কি কড়া পড়ে গেছে? আপনি কি অন্তর্জালের গোলকধাঁধায় পথ হারাইয়াছেন? সাইট থেকে সাইটান্তরে বাঁদরলাফ দিয়ে দিয়ে আপনি কি ক্লান্ত? বিরাট অঙ্কের টেলিফোন বিল কি জীবন থেকে সব সুখ কেড়ে নিচ্ছে? আপনার দুশ্চিন্তার দিন শেষ হল। ... আরও ...
- বুলবুলভাজা
- এ হল ক্ষমতাহীনের মিডিয়া। গাঁয়ে মানেনা আপনি মোড়ল যখন নিজের ঢাক নিজে পেটায়, তখন তাকেই বলে হরিদাস পালের বুলবুলভাজা। পড়তে থাকুন রোজরোজ। দু-পয়সা দিতে পারেন আপনিও, কারণ ক্ষমতাহীন মানেই অক্ষম নয়। বুলবুলভাজায় বাছাই করা সম্পাদিত লেখা প্রকাশিত হয়। এখানে লেখা দিতে হলে লেখাটি ইমেইল করুন, বা, গুরুচন্ডা৯ ব্লগ (হরিদাস পাল) বা অন্য কোথাও লেখা থাকলে সেই ওয়েব ঠিকানা পাঠান (ইমেইল ঠিকানা পাতার নীচে আছে), অনুমোদিত এবং সম্পাদিত হলে লেখা এখানে প্রকাশিত হবে। ... আরও ...
- হরিদাস পালেরা
- এটি একটি খোলা পাতা, যাকে আমরা ব্লগ বলে থাকি। গুরুচন্ডালির সম্পাদকমন্ডলীর হস্তক্ষেপ ছাড়াই, স্বীকৃত ব্যবহারকারীরা এখানে নিজের লেখা লিখতে পারেন। সেটি গুরুচন্ডালি সাইটে দেখা যাবে। খুলে ফেলুন আপনার নিজের বাংলা ব্লগ, হয়ে উঠুন একমেবাদ্বিতীয়ম হরিদাস পাল, এ সুযোগ পাবেন না আর, দেখে যান নিজের চোখে...... আরও ...
- টইপত্তর
- নতুন কোনো বই পড়ছেন? সদ্য দেখা কোনো সিনেমা নিয়ে আলোচনার জায়গা খুঁজছেন? নতুন কোনো অ্যালবাম কানে লেগে আছে এখনও? সবাইকে জানান। এখনই। ভালো লাগলে হাত খুলে প্রশংসা করুন। খারাপ লাগলে চুটিয়ে গাল দিন। জ্ঞানের কথা বলার হলে গুরুগম্ভীর প্রবন্ধ ফাঁদুন। হাসুন কাঁদুন তক্কো করুন। স্রেফ এই কারণেই এই সাইটে আছে আমাদের বিভাগ টইপত্তর। ... আরও ...
- ভাটিয়া৯
- যে যা খুশি লিখবেন৷ লিখবেন এবং পোস্ট করবেন৷ তৎক্ষণাৎ তা উঠে যাবে এই পাতায়৷ এখানে এডিটিং এর রক্তচক্ষু নেই, সেন্সরশিপের ঝামেলা নেই৷ এখানে কোনো ভান নেই, সাজিয়ে গুছিয়ে লেখা তৈরি করার কোনো ঝকমারি নেই৷ সাজানো বাগান নয়, আসুন তৈরি করি ফুল ফল ও বুনো আগাছায় ভরে থাকা এক নিজস্ব চারণভূমি৷ আসুন, গড়ে তুলি এক আড়ালহীন কমিউনিটি ... আরও ...
- টইপত্তর, ভাটিয়া৯, হরিদাস পাল(ব্লগ) এবং খেরোর খাতার লেখার বক্তব্য লেখকের নিজস্ব, গুরুচণ্ডা৯র কোন দায়িত্ব নেই। | ♦ : পঠিত সংখ্যাটি ১৩ই জানুয়ারি ২০২০ থেকে, লেখাটি যদি তার আগে লেখা হয়ে থাকে তাহলে এই সংখ্যাটি সঠিক পরিমাপ নয়। এই বিভ্রান্তির জন্য আমরা দুঃখিত।












