There are people who cultivate science … without looking for fame. – A. M. Legendre
।। ১ : আগন্তুক ।।
প্যারিস, ১৮০৬ সালের দ্বিতীয়ার্ধ। বিখ্যাত ফরাসি গণিতজ্ঞ এড্রিয়ান-মারি লেজানড্রার (Adrien-Marie Legendre) বাড়িতে তাঁর সাথে দেখা করতে এলেন অপরিচিত এক ব্যক্তি। লেজানড্রার হাতে একটা বই ধরিয়ে দিয়ে আগন্তুক বললেন, ‘বইটা যদি একবার পড়ে দ্যাখেন’। খানিক অবাক হয়ে লেজানড্রা জিজ্ঞাসা করলেন, ‘কি বই এটা?’ সসংকোচে আগন্তুক জানালেন, ‘আজ্ঞে, কাল্পনিক সংখ্যার (Imaginary number) উপর ... আমার নিজের কিছু মতামত’। ‘কাল্পনিক সংখ্যা!’ হালকা চমক লাগে লেজানড্রার। ‘বলে কি লোকটা! হালফিল গণিতের বেশ বিরল বিষয় এটা। লোকটাকে দেখে তো তেমন পণ্ডিত বলে মনে হয় না’ মনে মনে ভাবতে থাকেন লেজানড্রা। আগন্তুকের দিকে তীব্র অনুসন্ধানী দৃষ্টি নিক্ষেপ করে লেজানড্রা বলে উঠেন, ‘আচ্ছা, ... দেখব ক্ষণ পড়ে’। লেজানড্রার থেকে সদর্থক প্রত্যুত্তর পেয়ে আর কথা না বাড়িয়ে খুশি মনে দ্রুত স্থান ত্যাগ করেন আগন্তুক। লেজানড্রা তখন বইয়ের মলাটটা উল্টে প্রথম পাতার শিরোনামে নজর বুলাচ্ছেন : Essai sur une manière de représenter les quantités imaginaires dans les constructions géométriques (ইংরাজি : Essay on a method of representing imaginary quantities in geometric constructions)। আরে কি আশ্চর্য, লেখকের নাম কই? শিরোনামের নিচে তো কোনও লেখকের নাম ছাপা নেই! ‘আরে ও মশাই, লেখকের নাম ... !’ চোখ তুলে দেখেন সামনে তো কেউ দাঁড়িয়ে নেই। ভারি অদ্ভুত তো! লেখকের নাম নেই অথচ বই ছাপা হয়ে গেছে! এমন আবার হয় নাকি কখনও? বইটা আবার হাতে ধরিয়ে দিয়ে চলে গেল, নাম ধাম কিছু বলে গেল না! অবাক হয়ে লোকটার যাত্রা পথের দিকে তাকিয়ে রইলেন লিজানড্রা। ‘ঠিক আছে, বইটা ফেরত নিতে তো আসবে, ... আর পড়তে যখন দিয়েছে, একটা মতামত নিতে নিশ্চয় আসবে’ বিড় বিড় করতে থাকেন লিজানড্রা, ‘তখনই না হয় ওঁর নাম ঠিকানা জেনে নেব’।

লেখকের নামহীন সেই বই। পরে, নীচের অংশে কেউ লিখেছেন, Mr Argand, rue de Gentilly. (পর্ব ৩ দ্রষ্টব্য)
কিছুটা অনীহা নিয়েই বইটার পাতা উলটাতে থাকেন লিজানড্রা। বইটা যত পড়তে থাকেন, ততই বিস্ময়াবিষ্ট হয়ে উঠেন তিনি। কাল্পনিক সংখ্যাকে চমৎকার ভাবে জ্যামিতিক উপায়ে ব্যাখ্যা করেছেন লেখক। অভূতপূর্ব! এমন ব্যাখ্যা তো আগে কেউ কল্পনাই করতে পারেন নি। সত্যি বলতে কি, প্রথম দর্শনে লোকটা দেখে তিনিও ঠিক ঠাহর করতে পারেন নি যে এই লোকটা এমন জটিল বিষয় নিয়ে ভাবতে পারে। বইটা পড়ার পর এখন উলট কথাই ভাবতে হচ্ছে তাঁকে। এই বইটা পড়ার অভিজ্ঞতা নিয়ে পরে লিজানড্রা লিখেছেন, "At first I showed the author I was very doubtful, but I promised to read his memoir. I found contrary to my expectation, quite original ideas, very well presented, supported by a rather deep knowledge of calculation, …"। উচ্ছ্বসিত লিজানড্রা লেখকের দেখা পাওয়ার জন্য উন্মুখ হয়ে উঠেন। দিন যায়, সপ্তাহ যায়, কিন্তু সে লোক আর আসে না। মাস গড়িয়ে গেল, তাও তাঁর দেখা মেলে না। এ তো ভারি অদ্ভুত লোক! বইটা পড়তে বলে গেল, অথচ পাঠকের মতামত জানার কোনও তাগিদই নেই! কোনও তাগিদ নেই ফিরতি দেখা করার। উলটে লিজানড্রা নিজে এখন তাগিদ অনুভব করছেন। সোনার খনির থেকেও মূল্যবান সম্পদ রয়েছে যে তাঁর হাতে! এই খবরটা কাউকে না জানান পর্যন্ত স্বস্তি পাচ্ছেন না তিনি।
দক্ষিণ-পশ্চিম ফ্রান্সের মাইন্জ শহরে থাকেন তাঁর বিশিষ্ট বন্ধু, গণিতজ্ঞ ফঁসোয়া যসেফ ফঁসে (François Joseph Français)। ২ নভেম্বর ১৮০৬, ফঁসেকে গোটা বইটাই পাঠিয়ে দিলেন তিনি। একটা চিঠিতে লেখক ও তাঁর রচনা সম্পর্কে দু’কলম লিখেও দিলেন। কিন্তু মজার বিষয় হল, সে লেখক আর কোনও দিনও লিজানড্রা সাথে দেখা করতে আসেন নি। লিজানড্রা আবার সেই লেখকের নাম ঠিকানা কিছুই জানেন না। ফলে বেওয়ারিশের মতো সেই বই পড়ে রইল ফঁসোয়ার কাছে।
ঘটনার ৪ বছর পর, অক্টোবর ১৮১০ সালে মারা যান ফঁসোয়া। তখনও সেই বইয়ের লেখক বেপাত্তা। সেই বই তখনও পড়ে আছে ফঁসোয়ার দেরাজে। ফঁসোয়া মারা যাওয়ার আড়াই বছর পর, ফঁসোয়ার দেরাজে থেকে লিজানড্রার চিঠি সমেত সেই বই উদ্ধার করেন ফঁসোয়ার ভাই জাক ফ্রেদেরিচ ফঁসে (Jacques Frédéric Français)। পেশায় গণিতজ্ঞ ছিলেন জাক ফঁসেও। বইটা পড়ে তার মর্ম বুঝতে ভুল হয় নি জাকের। এতদিন ধরে গণিত চর্চা করছেন তিনি, কাল্পনিক সংখ্যা নিয়ে এমন অভিনব ব্যাখ্যার কথা তো আগে কখনও শোনেন নি! জাক বুঝতে পারেন এক অমূল্য সম্পদ রয়েছে তাঁর জিম্মায়। এই তত্ত্বকে এখনই জগতের সামনে তুলে ধরতে চান তিনি। প্যারিস থেকে তখন প্রকাশিত হতো যোসেফ ডিয়াজ জাগন (Joseph Diaz Gergonne) সম্পাদিত গণিতের নামজাদা মাসিক পত্রিকা ‘এনাল ডি ম্যাথামেটিক পিয়ো এট এ্যপ্লিকে’ (Annales de Mathématiques Pures et Appliquées)। সেপ্টেম্বর ১৮১৩, ‘এনাল’এ প্রকাশিত হল কাল্পনিক সংখ্যা নিয়ে জাক ফঁসের ১০ পাতার নিবন্ধ Nouveaux principes de Géométrie de position, et interprétation des symboles imaginaires (ইংরাজি : New Principles of Positional Geometry, and Interpretation of Imaginary Symbols)। লিজানড্রা চিঠি ও সেই বইয়ের প্রথম পাতা থেকে জাকের বিলক্ষণ জানা ছিল, গণিতের এমন যুগান্তকারী তত্ত্বের উদ্ভাবকের কোনও হদিশ নেই। নেই কোনও দাবীদারও। জাকের কাছে তাই সুযোগ ছিল সেই তত্ত্বকে নিজের আবিষ্কার বলে চালিয়ে দেওয়ার। প্রকাশনার জগতে এ তো আকছারই হয়ে থাকে। কিন্তু সে পথ মাড়ান নি জাক। নিবন্ধের শেষে ঋণ স্বীকার ও ন্যায় প্রতিষ্ঠার কথা উল্লেখ করে জাক লিখলেন, “I owe it, moreover, to justice to declare that the substance of these new ideas does not belong to me. I found them in a letter from M Legendre to my late brother …”।
এনালে জাকের নিবন্ধ প্রকাশ পাওয়ার পর, ঘটল অপ্রত্যাশিত এক ঘটনা। এনালের দপ্তরে চিঠি পাঠিয়ে এক সজ্জন জানালেন জাকের লেখা প্রবন্ধের আসল লেখক তিনি। অর্থাৎ তিনিই সেই ব্যক্তি, যিনি লিজানড্রাকে বইটা পড়তে দিয়েছিলেন। এই রচনা যে তাঁরই, তার প্রমাণ স্বরূপ রচনার মূল পাণ্ডুলিপিটা এনালের দপ্তরে প্রেরণ করেন পত্রলেখক। সেই পাণ্ডুলিপি পড়ে সম্পাদক বুঝলেন, এ তো অকাট্য প্রমাণ। না, কোনও সন্দেহ নেই যে, ইনিই সেই কাল্পনিক সংখ্যার লেখক। ৭ বছর পর কাল্পনিক সংখার সেই লেখকের হদিশ পাওয়া গেছে! মনে মনে উত্তেজনা অনুভব করতে থাকেন সম্পাদক জাগনও। কিন্তু, কে এই লেখক? কি তাঁর পরিচয়? লেখকের পাঠান সেই চিঠির নিচে দ্রুত চোখ বুলিয়ে দেখেন, চিঠির নিচে সাক্ষর করা- ‘আরগ্যান্ড’ (Argand)। আরগ্যান্ড হল একটা পদবী। ওই পদবীটুকুই শুধু লিখেছেন তিনি। পুরো নাম লেখেন নি। এরপর থেকে সারা পৃথিবীর গণিত প্রিয় মানুষের কাছে আরগ্যান্ড নামেই খ্যাত হয়ে উঠেন তিনি। তাঁর এই পদবী অনুসরণেই তাঁর সৃষ্ট কাল্পনিক তলের নাম দেওয়া হয় ‘আরগ্যান্ড প্লেন’।
।। ২ : ঘূর্ণন ।।
প্রাথমিক স্তরের ছাত্রছাত্রীরাও জানেন যে 25-এর বর্গমূল হল ± 5। এবার যদি জিগ্যেস করা হয় - 1-এর বর্গমূল কত, তাহলে কিন্তু অনেকেই সেই প্রশ্নের উত্তর দিতে পারবেন না। কারণটা খুবই সহজ, - 1-এর বর্গমূল নির্ণয় করাই যায় না। - 1 বা যে কোনও ঋণাত্মক সংখ্যার বর্গমূল নির্ণয়ের জন্য সচেষ্ট হয়েছিলেন বহু গণিতজ্ঞই, কিন্তু কেউই এই প্রশ্নের কোনও সদুত্তরই দিতে পারেন নি। ১৫৪৫ সালে এই বিষয়ে প্রথম ইতিবাচক আলোচনা করেন ইতালিয় গণিতজ্ঞ জেরোলামো কারদানো (Gerolamo Cardano)। ওই বছর প্রকাশিত তাঁর Artis Magnae, Sive de Regulis Algebraicis (ইংরাজি: The Great Art, or The Rules of Algebra) গ্রন্থের ৩৭ নম্বর অধ্যায়ে ত্রিঘাত সমীকরণ সমাধান প্রসঙ্গে ‘৫ যোগ মাইনাস ১৫-এর বর্গমূল’ এবং ‘৫ বিয়োগ মাইনাস ১৫-এর বর্গমূল’ বাক্য দু’টো ব্যবহার করেন। কারদানোর বক্তব্যর আধুনিক ভাষ্য রূপটা হল 5 + √(- 15) এবং 5 - √(- 15) । স্পষ্টতই ঋণাত্মক সংখ্যার বর্গমূলের উল্লেখ করেছেন তিনি। এখান থেকেই ঋণাত্মক সংখ্যার বর্গমূল বা কাল্পনিক সংখ্যার ইতিহাসের সূত্রপাত। বছর ৩০ পর, ১৫৭২ সালে প্রকাশিত হয় আরেক ইতালিয় গণিতজ্ঞ রাফায়েল বোমবেল্লির (Rafael Bombelli) গ্রন্থ L'Algebra Parte maggiore dell Arimetica (ইংরাজি: Algebra, a major Part of Arithmetic)। এই গ্রন্থে কাল্পনিক সংখ্যার গুণের নিয়ম ব্যাখ্যা প্রসঙ্গে তিনি যা লেখেন তার ভাবানুবাদ হল, ‘ঋণাত্মক সংখ্যার বর্গমূলের সাথে ঋণাত্মক সংখ্যার বর্গমূল গুণ করলে ওই ঋণাত্মক সংখ্যা পাওয়া যায়’। বোমবেল্লির বক্তব্যর আধুনিক ভাষ্য রূপ হল, √(- n) x √(- n) = - n। গণিতশাস্ত্রের ইতিহাসে অত্যন্ত গুরুত্বপূর্ণ সূত্র এটা। কারণ, √(- n) কাল্পনিক সংখ্যা হলেও, তাদের গুণফল - n কিন্তু বাস্তব সংখ্যা। বিষয়টা যথেষ্টই প্রণিধানযোগ্য। কারণ, দুটো কাল্পনিক সংখ্যার গুণফল আর কাল্পনিক সংখ্যা থাকছে না। সেটা বাস্তব সংখ্যা হয়ে যাচ্ছে। বিষয়টা আরও পরিষ্কার করে ফুটে উঠে ফরাসি গণিতজ্ঞ রেনে দেকার্তের (Rene Descartes) আলোচনা থেকে। ১৬৩৭ সালে প্রকাশিত হয় দেকার্তের গ্রন্থ La Geometrie (ইংরাজি: Geomerty)। এই গ্রন্থে কার্তেসিয় জ্যামিতি বা স্থানাঙ্ক জ্যামিতির উপস্থাপনা করেন তিনি, সহজ ভাষায় যাকে আমরা গ্রাফ বলে থাকি। স্থানাঙ্ক জ্যামিতিতে বা গ্রাফে, দুটো লম্ব অক্ষ টানা হয়, যার পরস্পরকে মূলবিন্দুতে ছেদ করে। মূলবিন্দুর উভয়দিকে সমদূরত্বে বিভিন্ন ধনাত্মক ও ঋণাত্মক সংখ্যা স্থাপন করা হয়। তাঁর সৃষ্ট এই X ও Y অক্ষ দু’টোর উপর সমস্ত সংখ্যাকে স্থান দিতে পারলেও - 1-এর বর্গমূলকে কোথাও স্থান দিতে পারেন নি। অনেক ভাবনা চিন্তার পর তিনি বললেন, - 1-এর বর্গমূল হল একটা কাল্পনিক সংখ্যা। সেই সংখ্যাকে সংখ্যারেখার ওপর স্থাপন করা যায় না বা জ্যামিতিক উপায়ে ব্যাখ্যা করা যায় না। উল্লেখ্য, দেকার্তেই হলেন প্রথম গণিতজ্ঞ যিনি 'Imaginary number' (কাল্পনিক সংখ্যা) কথাটা ব্যবহার করেন।
দেকার্তের মতানুসারে √(- n) হল কাল্পনিক সংখ্যা এবং একে গ্রাফ কাগজে স্থাপন করা যায় না। অথচ বোমবেল্লি বলেছেন √(- n) x √(- n) = - n = বাস্তব সংখ্যা। তাহলে √(- n) x √(- n) কে তো নিশ্চয় গ্রাফ কাগজে স্থাপন করা সম্ভব। আর ঠিক এই বিষয়টা নিয়েই ধন্ধে পড়ে যান গণিতজ্ঞরা। একটাই গ্রাফে কি করে কাল্পনিক সংখ্যা আর বাস্তব সংখ্যাকে স্থান দেওয়া সম্ভব? ১৭০৭ সালে কাল্পনিক সংখ্যার তত্ত্বকে বিস্তার ঘটিয়ে বিষয়টার সাথে ত্রিকোণমিতি যুক্ত করে (cos θ + i sin θ )n –এর সূত্রটা লিপিবদ্ধ করেন ফরাসি গণিতজ্ঞ আব্রাহাম ডি মোয়েভার (Abraham de Moivre)। এর ফলে বিষয়টা আবার বেশ ভারী ও জটিল হয়ে উঠে। বিপরীতে, কাল্পনিক সংখ্যার চর্চাকে আমজনতার জন্য সহজতর তোলেন সুইস গণিতজ্ঞ লিওনহার্ড অয়লার (Leonhard Euler)। ১৭৭৭ সালে তিনিই প্রথম – 1-এর বর্গমূলকে ইংরাজি i অক্ষর দিয়ে চিহ্নিত করেন। এতে কাল্পনিক সংখ্যার যোগ-বিয়োগ-গুণ-ভাগ সহজতর হয়ে উঠে। যেমন, i + i = 2i, কিম্বা 7i - 4i = 3i ইত্যাদি। এখন আমরা বলতেই পারি, i = √(- 1) হলে i2 = - 1 হবে। এই - 1 কিন্তু বাস্তব সংখ্যা, যা সংখ্যারেখায় দিব্যি স্থাপন করা যাচ্ছে। আবার i3 = i2 x i = - 1 x i = - i = কাল্পনিক সংখ্যা, কিন্তু i4 = i2 x i2 = (- 1) x (– 1) = 1 = বাস্তব সংখ্যা। দেখা যাচ্ছে, সূচকের মান বৃদ্ধির সাথে সাথে বাস্তব ও অবাস্তব সংখ্যায় পরিবর্তিত হয় চলেছে i। in-এর বাস্তব মানগুলোকে না হয় সংখ্যারেখায় স্থাপন করা সম্ভব, কিন্তু অবাস্তব মানগুলোকে কি ভাবে সাংখ্যারেখায় স্থাপন করা যায়? আর ঠিক এই সমস্যাটারই সমাধান করে ফেলেছিলেন আরগ্যান্ড। তিনিই প্রথম যিনি একই গ্রাফ কাগজের ওপর বাস্তব এবং অবাস্তব সংখ্যাকে স্থাপন করতে সক্ষম হয়েছিলেন। তবে আরগ্যান্ডের কাজটা কিছুটা সহজ করে দিয়েছিলেন জার্মান গণিতজ্ঞ কার্ল ফ্রেডরিচ গাওস (Johann Carl Friedrich Gauss)। কাল্পনিক সংখ্যার ইতিহাসের গোড়াতেই কারদানো 5 + √(- 15) সংখ্যাটা ব্যবহার করেছিলেন। লক্ষণীয় √(- 15) অবাস্তব বা কাল্পনিক হলেও 5 কিন্তু বাস্তব সংখ্যা। ১৭৯৭ সালে গাওস বললেন, বাস্তব ও অবাস্তব সংখ্যার সংমিশ্রণে a + ib আকারে যে সংখ্যা উৎপন্ন হয় তাকে জটিল রাশি (complex number) বলা হয়, যেখানে a ও b বাস্তব সংখ্যা কিন্তু i অবাস্তব সংখ্যা। এখানে খেয়াল রাখা প্রয়োজন, কেবলমাত্র i-কে কাল্পনিক সংখ্যা বা অবাস্তব সংখ্যা বলা হয়, বিপরীতে a + ib-কে বলা হয় জটিল রাশি।
এই a + ib আকার বা জটিল রাশিই আরগ্যান্ডের ভাবনাকে প্রভাবিত করেছিল। আরগ্যান্ড বললেন, গ্রাফ কাগজের X-অক্ষটাকে বাস্তব অক্ষ আর Y-অক্ষটাকে অবাস্তব অক্ষ ধরা হোক আর a + ib কে কার্তেসিয় স্থানাঙ্কের মত (a, ib) ভাবা হোক। যে কোনও জটিল রাশিকে তাহলে সহজেই গ্রাফ কাগজে স্থাপন করা সম্ভবপর হবে। আরগ্যান্ড প্রস্তাবিত বাস্তব অক্ষ আর অবাস্তব অক্ষ সম্বলিত এই কাল্পনিক তলই পরবর্তীকালে ‘আরগ্যান্ড প্লেন’ নামে পরিচিত হয়।
দেকার্তে প্রস্তাবিত কার্তেসিয় জ্যামিতিতে X-অক্ষকে ঘড়ির কাঁটার বিপরীত দিকে ৯০ ডিগ্রি ঘোরালে Y-অক্ষ পাওয়া যায়। আরগ্যান্ড প্রস্তাব দিলেন, ঘড়ির কাঁটার বিপরীত দিকে প্রতিটি ৯০ ডিগ্রি ঘূর্ণনের অর্থ সংখ্যাকে i দিয়ে গুণ করার সমতুল্য ধরতে হবে। X-অক্ষের ওপর 1 একক দৈর্ঘ্যকে ঘড়ির কাঁটার বিপরীত দিকে ৯০ ডিগ্রি ঘোরানোর অর্থ, 1 কে i দিয়ে গুণ করার সমতুল্য। অর্থাৎ 1 x i = 1i = i যা অবাস্তব সংখ্যা এবং যা Y-অক্ষ বা অবাস্তব অক্ষের ওপর অবস্থিত হবে। Y-অক্ষের ওপর অবস্থিত এই i একক দৈর্ঘ্যকে ফের ঘড়ির কাঁটার বিপরীত দিকে ৯০ ডিগ্রি ঘোরানোর অর্থ i কে পুনরায় i দিয়ে গুণ করার সামিল। এবার i x i = i2 = - 1 যা বাস্তব এবং যা X-অক্ষ বা বাস্তব অক্ষের ঋণাত্মক দিকের ওপর অবস্থিত। অনুরূপে X-অক্ষের ঋণাত্মক দিকের ওপর অবস্থিত - 1 একক দৈর্ঘ্যকে ফের ঘড়ির কাঁটার বিপরীত দিকে ৯০ ডিগ্রি ঘোরানোর অর্থ - 1 কে i দিয়ে গুণ করা। এবার - 1 x i = - 1i = - i যা অবাস্তব এবং যা Y-অক্ষ বা অবাস্তব অক্ষের ঋণাত্মক দিকের ওপর অবস্থিত। পরিশেষে, Y-অক্ষের ঋণাত্মক দিকের ওপর অবস্থিত - i একক দৈর্ঘ্যকে ঘড়ির কাঁটার বিপরীত দিকে আবার ৯০ ডিগ্রি ঘোরালে - i কে ফের i দিয়ে গুণ করতে হবে। সেক্ষেত্রে - i x i = - i2 = - (-1) = 1 যা বাস্তব এবং যা X-অক্ষের ধনাত্মক দিকের ওপর পূর্বের অবস্থানে ফিরে আসবে, সম্পূর্ণ হবে একটা বৃত্তাকার পরিক্রমণ।
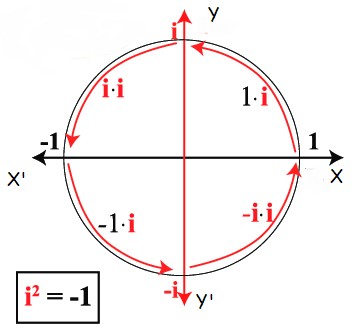
ঘড়ির কাঁটার বিপরীত দিকে প্রতিটি ৯০ ডিগ্রি ঘূর্ণনের অর্থ সংখ্যাকে i দিয়ে গুণ করার সমতুল্য।
কাল্পনিক সংখ্যাকে তাঁর গ্রাফে স্থান দিতে পারেন নি দেকার্তে। ৯০ ডিগ্রি ঘূর্ণনকে i দিয়ে গুণ করার সমতুল্য ধরে সেই সমস্যার সমাধান করে দিলেন আরগ্যান্ড। খুলে গেল দীর্ঘ দিন ধরে অমীমাংসিত গণিতের এক সমস্যার জট। আরগ্যান্ডের এই সমাধানকে ingenious and profound বলে আখ্যা দিয়েছেন স্কটিশ গণিতবিদ জর্জ ক্রিস্টাল। এহেন ingenious মানুষটা কিন্তু তখনও লোকচক্ষুর অন্তরালেই রয়ে গেছেন। তবে তাঁর মহিমা ছুঁয়ে গেছে প্রতিটি গণিতপ্রেমীকে। অজ্ঞাত এক গণিতপ্রেমী তাই আরগ্যান্ড কে নিয়ে গান বেঁধেছেন (প্রথম স্তবকের ভাবানুবাদ)-
দেখেছি আরগ্যান্ড তলের মহিমার ছটা
আমি দেখেছি ডি মোয়েভারের i ও থিটা
বড় অনিন্দ্য প্রাণবন্ত জটিল মূল
আর এই মাইনাস একের বর্গমূল
জটিল রাশি কি সরল
জটিল রাশি কি সরল
জটিল রাশি কি সরল।
।। ৩ : কাল্পনিক ।।
অবাস্তব সংখ্যা নিয়ে আরগ্যান্ডের বই প্রকাশের প্রায় ৭০ বছর পরের কথা। ১৮৭৪ সালে জটিল রাশি সংক্রান্ত যাবতীয় তত্ত্বকে একত্রিত করে চার খণ্ডের এক পুস্তক প্রকাশ করেন ফরাসি গণিতজ্ঞ গিওম-জুল উয়েল (Guillaume-Jules Hoüel)। জটিল রাশি নিয়ে এত বিস্তারিত কাজ ইতিপূর্বে কখনও হয় নি। জটিল রাশি নিয়ে কাজ করতে গিয়ে উয়েল দেখলেন, জটিল রাশির উপর গুরুত্বপূর্ণ অবদান রেখে গেছেন আরগ্যান্ড। অথচ আরগ্যান্ড সম্পর্কে তেমন কিছু জানেন না কেউই। অবাস্তব সংখ্যার এই উপেক্ষিত নায়কের জীবনী লেখার উদ্যোগ নিলেন উয়েল। কিন্তু অনেক খোঁজাখুঁজি করেও আরগ্যান্ড সম্পর্কে কোনও তথ্যই সংগ্রহ করতে পারলেন না তিনি। আগামী প্রজন্মকে কী তবে আরগ্যান্ড সম্পর্কে কিছুই জানিয়ে যেতে পারবেন না তিনি? বিষয়টা ভেবেই খানিকটা যেন মুষড়েই পড়লেন উয়েল। সাতপাঁচ ভাবতে ভাবতে হঠাৎই তাঁর আমি আরগ্যান্ডের (Ami Argand) নামটা মনে পড়ে। পদার্থবিদ ও রসায়নবিদ হিসেবে পরিচিত আমি আরগ্যান্ড প্যারিসের বাসিন্দা ছিলেন। আঠেরো শতকের শেষের এক বিশেষ ধরণের ল্যাম্প প্রস্তুত করে সাড়া ফেলে দিয়েছিলেন তিনি। এহেন আমি আরগ্যান্ড আদতে কিন্তু ফরাসি নাগরিক ছিলেন না। আমি আরগ্যান্ডের আদি বাড়ি ছিল সুইৎজারল্যান্ডের জেনেভাতে। শিক্ষা ও কর্মসূত্রে প্যারিসে আসেন তিনি। আমি আরগ্যান্ডের নামটা মনে পড়তেই, উয়েলের মনে হল, গণিতের এই অখ্যাত আরগ্যান্ডের আদি বাড়িও জেনেভাতে হলেও হতে পারে। জেনেভাতে তাঁর অনেক বন্ধুবান্ধব থাকেন। তাঁদের কাছ থেকে আরগ্যান্ড সম্পর্কে খোঁজখবর নিয়ে দেখা যেতেই পারে। উয়েলের এমনই এক বন্ধু হলেন এম. আর. উল্ফ (M. R. Wolf)। সুইৎজারল্যান্ডের বিজ্ঞানের ইতিহাস নিয়ে প্রগাঢ় পাণ্ডিত্য রয়েছে উল্ফের। এহেন উল্ফের সাথে পত্র মারফৎ সত্বর যোগাযোগ করলেন উয়েল। জানালেন, গণিতবিদ আরগ্যান্ড ও তাঁর বংশ সম্পর্কে বিস্তারিত তথ্য জানতে চান তিনি। উয়েলের পত্র পেয়ে আরগ্যান্ড সম্পর্কে খোঁজখবর নিতে শুরু করলেন উল্ফ। অনেক খোঁজাখুঁজির পর জনৈক জঁ-রবার্ট আরগ্যান্ড (Jean-Robert Argand) নামের এক ব্যক্তির খোঁজ পেলেন তিনি, ১৮০৬ সাল নাগাদ যিনি প্যারিসেই থাকতেন বলে জানা যাচ্ছে। কিন্তু এই জঁ-রবার্ট আরগ্যান্ডই যে সেই গণিতবিদ আরগ্যান্ড তার তেমন কোনও নিশ্চয়তা কিন্তু পেলেন না তিনি। কারণ বহু জেনেভাবাসীই কর্মসূত্রে প্যারিসে বসবাস করতেন এবং এখনও করেন। তাঁদের অনেকেরই পদবী আবার আরগ্যান্ড। তবু, যেটুকু তথ্য সংগ্রহ করতে পেরেছেন, সেই তথ্যটুকুই উয়েলকে পাঠিয়ে দিলেন তিনি। সাথে এটা জানাতে ভুললেন না যে, এই তথ্য কিন্তু সংশয়হীন নয়।
আরগ্যান্ডের জীবনী প্রকাশ করতে তখন যেন বদ্ধপরিকর ছিলেন উয়েল। ফলে উল্ফের পাঠানো সেই তথ্যকে প্রামাণ্য বলে ধরে নিলেন তিনি। ১৮৭৪ সালে অবাস্তব সংখ্যা নিয়ে আরগ্যান্ডের লেখা মূল পুস্তিকাটা পুনঃপ্রকাশ করলেন উয়েল। সেই বইয়ের শুরুতে ১২ পাতার এক মুখবন্ধ সংযোজন করেন তিনি। সেই মুখবন্ধের শেষ দুটো অনুচ্ছেদে মাত্র ২২ লাইনের মধ্যে আরগ্যান্ডের জীবনী লিপিবদ্ধ করলেন। উয়েল লিখিত আরগ্যান্ডের সেই জীবনীর সারাংশ এই রকম :
১৮ জুলাই ১৭৬৮ সালে জেনেভায় জন্মগ্রহণ করেন জঁ-রবার্ট আরগ্যান্ড। তাঁর বাবার নাম জাক আরগ্যান্ড ও মায়ের নাম ইভ কানাক। পেশাগত ভাবে একজন একাউন্টটেন্ট ছিলেন জঁ-রবার্ট আরগ্যান্ড। গণিত চর্চা ছিল তাঁর নেশা। ১৮০৬ সালের আগেই প্যারিসে চলে আসেন আরগ্যান্ড। এখানে একটা বইয়ের দোকান খোলেন তিনি এবং প্যারিসেই পরিবার নিয়ে স্থায়ীভাবে বসবাস করতে শুরু করেন। পরিবার বলতে, আরগ্যান্ডের এক পুত্র এবং এক কন্যা সন্তানের কথা জানা যায়। তাঁর পুত্রের নাম জানা যায় না। তাঁর মেয়ের নাম জান-ফঁসোয়া-দোহুথি-মারি-এলিসাবেথ আরগ্যান্ড। জার্মানির স্টুটগার্ট শহরের জনৈক ফেলিক্স বুসকেটকে বিবাহ করেন এলিসাবেথ। প্যারিস শহরেই শেষ নিশ্বাস ত্যাগ করেন গণিতজ্ঞ জঁ-রবার্ট আরগ্যান্ড।
এই পর্যন্ত উল্লেখ করা তথ্যগুলো উলফের কাছ থেকে সংগ্রহ করেছিলেন উয়েল। এরপর নিজের এক সূত্র উদ্ধৃত করে উয়েল জানাচ্ছেন, ১৮১৩ সাল নাগাদ প্যারিসের দক্ষিণ শহরতলির ১২ রুই ডি জঁতিই (rue de Gentilly) তে থাকতেন আরগ্যান্ড। সেই সময়ে ‘এনাল’ পত্রিকার সম্পাদক জাগনের কাছে যে মূল পাণ্ডুলিপিটা পাঠিয়েছিলেন আরগ্যান্ড, সেই পাণ্ডুলিপিতে স্বহস্তে নিজের বাড়ির এই ঠিকানা লিখে দিয়েছিলেন বলেই জানালেন উয়েল।
উয়েল লিখিত এই ছত্রকটাই আজ পর্যন্ত পাওয়া আরগ্যান্ডের একমাত্র জীবনী। গত ১৫০ বছর ধরে এই জীবনীটাই প্রশ্নাতীত ভাবে সর্বত্র গৃহীত ও প্রচারিত হয়েছে। ১৯৯০ সাল নাগাদ আরগ্যান্ডকে নিয়ে পুনরায় তদন্তে নামেন জার্মান গণিত-ইতিহাসবিদ গার্ট শ্চুবরিং (Gert Schubring)। না, আরগ্যান্ড সম্পর্কে নতুন কোনও তথ্যই সামনে আনতে পারেন নি শ্চুবরিং। তবে একটা বিষয়ে তিনি নিশ্চিত করলেন আমাদের। আরগ্যান্ডের জীবনীর যেটুকু অংশ আমরা জানতে পেরেছি, তা প্রমাণ সাপেক্ষ। তিনি বললেন- ‘these few known data seem to be doubtful’। অন্য কিছু গবেষকরা আবার আরগ্যান্ডের জন্মসাল নিয়ে প্রশ্ন তুললেন। তাঁরা বললেন, উয়েলের বক্তব্য অনুসারে ১৭৬৮ সালে জন্মগ্রহণ করেছিলেন আরগ্যান্ডের। সেই হিসেবে ১৮০৬ সালে তাঁর বয়স দাঁড়ায় ৩৮ বছর। ১৮০৬ সালেই লিজানড্রার সাথে দেখা করেছিলেন আরগ্যান্ড। ফঁসোয়া যসেফ ফঁসেকে লেখা তাঁর চিঠিতে আরগ্যান্ডকে ‘ইয়ং’ বলে বর্ণনা করেছেন লিজানড্রা। গবেষকরা প্রশ্ন করেন, ৩৮ বছরের কোনও মানুষকে দেখে কি ‘ইয়ং’ বলে মনে হতে পারে? এই প্রশ্নটাকে সামনে রেখেই কিছু গবেষক মনে করেন আরগ্যান্ডের জন্মসালটা আদৌ সঠিক নয়। সঠিক নয় জন্মদিনটাও। এই সমস্ত দোলাচলের মধ্যে আরগ্যান্ড সম্পর্কে একটা মতামত ক্রমেই প্রবল হতে থাকে। সেই মতানুসারে, গণিতবিদ আরগ্যান্ড আর উয়েল উল্লিখিত জঁ-রবার্ট আরগ্যান্ড মোটেও এক ব্যক্তি নন। না তিনি কোনও একাউন্টটেন্ট ছিলেন, না তিনি ছিলেন কোনও পুস্তক বিক্রেতা। তাঁর ঘর-বাড়ি, ছেলে-মেয়ে সম্পর্কে কোনও তথ্যই গ্রহণযোগ্য নয়।
বোঝো কাণ্ড! আরগ্যান্ড সম্পর্কে যেটুকু তথ্য আমরা জানতাম সেটাও নাকি ভুলে ভরা! তাহলে আরগ্যান্ড সম্পর্কে আমরা কি কিছুই জানি না? জবাবে গবেষকরা বললেন, হ্যাঁ জানি তো। ১৮০৬ থেকে ১৮১৩ সাল পর্যন্ত প্যারিসে থাকতেন আরগ্যান্ড। এই সময়কালের আগের ও পরের তথ্য সমূহ প্রমাণ সাপেক্ষ। ১৮০৬ সালে কাল্পনিক সংখ্যা নিয়ে তাঁর মতামত লিপিবদ্ধ করেন আরগ্যান্ড। নিজের উদ্যোগে গুটিকয়েক বই ছাপিয়ে ছিলেন তিনি। অল্প কয়েকজনের মধ্যে বণ্টন করেছিলেন সেই বইগুলো। সেই বইয়ের এক কপি পড়তে দিয়েছিলেন লিজানড্রাকে। লিজানড্রা একবার মাত্র চাক্ষুষ করেছিলেন আরগ্যান্ডকে। লিজানড্রা ছাড়া তেমন আর কেউই আরগ্যান্ডকে প্রত্যক্ষ করেন নি। তাঁকে চিনতেন না প্রায় কেউই। এবং আজও তাঁকে চেনেন না কেউই। অথচ তিনিই আমাদের চিনিয়ে দিয়ে গেলেন ‘আরগ্যান্ড প্লেন’। তাঁর সৃষ্ট এই কাল্পনিক তলের মতোই তাঁর জীবনীর অধিকাংশ ঘটনাই যেন কাল্পনিক। তাঁর জীবনের কিছুটা অংশ X-অক্ষের মতো বাস্তব আর কিছুটা অংশ Y-অক্ষের মতো কাল্পনিক। ধরা দিয়েও বাস্তব জগতের কাছে অধরাই রয়ে গেলেন কাল্পনিক পুস্তক বিক্রেতা আরগ্যান্ড।
– i –
পুনঃপ্রকাশ সম্পর্কিত নীতিঃ এই লেখাটি ছাপা, ডিজিটাল, দৃশ্য, শ্রাব্য, বা অন্য যেকোনো মাধ্যমে আংশিক বা সম্পূর্ণ ভাবে প্রতিলিপিকরণ বা অন্যত্র প্রকাশের জন্য গুরুচণ্ডা৯র অনুমতি বাধ্যতামূলক।
 There are people who cultivate science … without looking for fame. – A. M. Legendre
There are people who cultivate science … without looking for fame. – A. M. Legendre 

 dc | 2401:4900:1f2b:b0c2:7c45:ef34:5e22:***:*** | ১৮ জানুয়ারি ২০২৪ ২০:৪৭527743
dc | 2401:4900:1f2b:b0c2:7c45:ef34:5e22:***:*** | ১৮ জানুয়ারি ২০২৪ ২০:৪৭527743 শুভদীপ | 2402:3a80:1132:75e4:d4ef:91ff:fe1e:***:*** | ১৮ জানুয়ারি ২০২৪ ২২:৫৬527744
শুভদীপ | 2402:3a80:1132:75e4:d4ef:91ff:fe1e:***:*** | ১৮ জানুয়ারি ২০২৪ ২২:৫৬527744সমরেশ মুখার্জী | ১৮ জানুয়ারি ২০২৪ ২৩:৩৮527745
সমরেশ মুখার্জী | ১৯ জানুয়ারি ২০২৪ ০০:৫৭527747
Arindam Basu | ১৯ জানুয়ারি ২০২৪ ০২:৪৬527750
 dc | 2401:4900:1cd1:9fe:f846:737:cdcf:***:*** | ১৯ জানুয়ারি ২০২৪ ০৮:২৬527752
dc | 2401:4900:1cd1:9fe:f846:737:cdcf:***:*** | ১৯ জানুয়ারি ২০২৪ ০৮:২৬527752দ | ১৯ জানুয়ারি ২০২৪ ০৮:৫৬527754
রমিত চট্টোপাধ্যায় | ১৯ জানুয়ারি ২০২৪ ১২:১৮527766
Sahasralochan Sharma | ১৯ জানুয়ারি ২০২৪ ১৯:৪৪527775
 dc | 171.79.***.*** | ১৯ জানুয়ারি ২০২৪ ১৯:৫১527776
dc | 171.79.***.*** | ১৯ জানুয়ারি ২০২৪ ১৯:৫১527776সমরেশ মুখার্জী | ১৯ জানুয়ারি ২০২৪ ২১:৪৮527778
দ | ১৯ জানুয়ারি ২০২৪ ২১:৫৫527781
প্যালারাম | ১৯ জানুয়ারি ২০২৪ ২২:১৬527783

সমরেশ মুখার্জী | ২০ জানুয়ারি ২০২৪ ০০:২৭527790
Prabhas Sen | ২০ জানুয়ারি ২০২৪ ০৯:৪৮527803
 dc | 171.79.***.*** | ২০ জানুয়ারি ২০২৪ ১০:২৯527807
dc | 171.79.***.*** | ২০ জানুয়ারি ২০২৪ ১০:২৯527807
Ranjan Roy | ২৪ জানুয়ারি ২০২৪ ০৬:৫৮527928
নিরমাল্লো | ২৭ জানুয়ারি ২০২৪ ১১:১০527972
Sahasralochan Sharma | ২৮ জানুয়ারি ২০২৪ ১৩:২৭527989
Sahasralochan Sharma | ২৮ জানুয়ারি ২০২৪ ১৩:২৮527990
Sahasralochan Sharma | ২৮ জানুয়ারি ২০২৪ ১৩:৩১527991
Sahasralochan Sharma | ২৮ জানুয়ারি ২০২৪ ১৩:৩৪527992
Sahasralochan Sharma | ২৮ জানুয়ারি ২০২৪ ১৩:৩৬527993
 Ekak | 103.157.***.*** | ০৭ ফেব্রুয়ারি ২০২৪ ১৮:৫৬528274
Ekak | 103.157.***.*** | ০৭ ফেব্রুয়ারি ২০২৪ ১৮:৫৬528274
 অন্ধকারের অনুশাসন ও শব্দের শৃঙ্খলা : শুভদীপ মণ্ডল
অন্ধকারের অনুশাসন ও শব্দের শৃঙ্খলা : শুভদীপ মণ্ডল মধুবাতা ঋতায়তে : শারদা মণ্ডল
মধুবাতা ঋতায়তে : শারদা মণ্ডল দিন গোনার দিন ৭ : হীরেন সিংহরায়
দিন গোনার দিন ৭ : হীরেন সিংহরায় কাদামাটির হাফলাইফ - ইট পাথরের জীবন : ইমানুল হক
কাদামাটির হাফলাইফ - ইট পাথরের জীবন : ইমানুল হক তিরিশ দিন অথবা এক কোটি ষোল লক্ষ ঘন্টা: শিক্ষা-ব্যবস্থার এক ভয়ঙ্কর জটিল অঙ্ক : সীমান্ত গুহঠাকুরতা
তিরিশ দিন অথবা এক কোটি ষোল লক্ষ ঘন্টা: শিক্ষা-ব্যবস্থার এক ভয়ঙ্কর জটিল অঙ্ক : সীমান্ত গুহঠাকুরতা দুই দাপুটের কাশীভ্রমণ - ২ : দ
দুই দাপুটের কাশীভ্রমণ - ২ : দ নির্বাচন ২০২৬! : bikarna
নির্বাচন ২০২৬! : bikarna উপরের ১ বনাম উপরের ১০ : Barnali Mukherjee
উপরের ১ বনাম উপরের ১০ : Barnali Mukherjee পাউডার বনাম ধুলো ঘাম : মালবিকা মিত্র
পাউডার বনাম ধুলো ঘাম : মালবিকা মিত্র এক যে ছিলেন রাজা - ৯ম পর্ব : Kishore Ghosal
এক যে ছিলেন রাজা - ৯ম পর্ব : Kishore Ghosal অনির্বাণ এখনও গ্রীনকার্ড পায়নি : c
অনির্বাণ এখনও গ্রীনকার্ড পায়নি : c পদ্য: দুটো গ্লাস টেবিলেই : Amitava Mukherjee
পদ্য: দুটো গ্লাস টেবিলেই : Amitava Mukherjee এবার @ dc : albert banerjee
এবার @ dc : albert banerjee এবার নবারুণ জাপটা : albert banerjee
এবার নবারুণ জাপটা : albert banerjee কালো বাগান AI, ও মলয় রায়চৌধুরী : albert banerjee
কালো বাগান AI, ও মলয় রায়চৌধুরী : albert banerjee











