- বুলবুলভাজা ধারাবাহিক শিক্ষা শনিবারবেলা

-
সিম্পসন’স প্যারাডক্স
যদুবাবু
ধারাবাহিক | শিক্ষা | ১৭ এপ্রিল ২০২১ | ৮৭৬৪ বার পঠিত | রেটিং ৫ (৫ জন) - প্রথম কিস্তি | দ্বিতীয় কিস্তি | তৃতীয় কিস্তি | চতুর্থ কিস্তি | পঞ্চম কিস্তি | ষষ্ঠ কিস্তি | সপ্তম কিস্তি | অষ্টম কিস্তি | সমষ্টি থেকে ব্যষ্টি | ভক্স পপুলি | দুই লেজান্ড্রর গল্প | বিষের ইতিহাস, ইতিহাসের বিষ১.
একটা ধাঁধার মত ছোট্ট অঙ্ক দিচ্ছি, মন দিয়ে শুনুন।
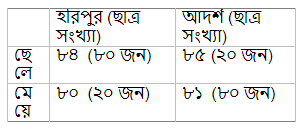
ধরা যাক, আপনার পাড়ায় দুটো ইস্কুল, আদর্শ বিদ্যানিকেতন আর হরিপুর মেমোরিয়াল। দুই স্কুলের খুব রেষারেষি, কে কার থেকে বেশী ভালো সেই নিয়ে বিতণ্ডার শেষ নেই। আপনি আবার এই পাড়ার মোড়ল, ঠিক করলেন, একটু খতিয়ে দেখবেন কোথায় কত নম্বর উঠেছে বোর্ডের পরীক্ষায়। দেখতে গিয়ে যা পেলেন, তা হচ্ছে এই – হরিপুরের ছেলেরাও আদর্শের থেকে গড় নম্বর পেয়েছে বেশী, আবার মেয়েরাও বেশী… ধরা যাক, তাদের গড় নম্বর এই রকম (সব-ই মনগড়া)।আপনি এই অব্দি দেখে লিখতে যাচ্ছেন ছেলে-মেয়ে দুই বিভাগেই আদর্শ একটু এগিয়ে, এমন সময় হরিপুরের হেডমাস্টার জিগ্যেস করে বসলেন, আলাদা-আলাদা করে নয়, সব মিলিয়ে কার কত? কী আশ্চর্য কাণ্ড, সব মিলিয়ে দেখলে হরিপুরের গড়ঃ ৮৩.২ আর আদর্শের গড়ঃ ৮১.৮ !
মানে সোজা কথায়, ছেলে-মেয়ে মিশিয়ে দেখলে হরিপুর এগিয়ে, অথচ আলাদা-আলাদা করে আদর্শ? এ কী করে সম্ভব?
মনগড়া আর-ও একটা উদাহরণ দিই? তবে এটা আমার বানানো নয়, বেকার ও ক্রেমার-বাবুর পেপার৪,৫ থেকে তোলা রীতিমত।টেবিল-টা মন দিয়ে দেখুন। দুটি ট্রিটমেন্ট, এবং আগের মতন দুটিই গ্রূপ – পুরুষ-নারী। প্রথম সারিতে বলছে, শুধু পুরুষদের চিকিৎসায় ট্রিটমেন্ট ‘এ’-র সার্ভাইভাল রেট ৬০%, আর ‘বি’ এর কম (৫০%), আবার শুধু নারীদের চিকিৎসায়, ‘এ’ এবং ‘বি’ এর সার্ভাইভাল রেট যথাক্রমে ৯৫% ও ৮৫%, অর্থাৎ এই বেলাতেও ‘বি’-এর থেকে ‘এ’ ভালো?
এইবার একদম শেষ সারি-টি দেখুন – কম্বাইন করে দেখলে, উলটে গেছে হিসেবনিকেশ – সব মিলিয়ে ‘বি’ ৮০% আর ‘এ’ মাত্র ‘৭২%’। পেপারের টাইটেল ধার করে বললে, “গুড ফর উইমেন, গুড ফর মেন, ব্যাড ফর পিপল”?
এইবারে ধরুন আপনি ডাক্তার অথবা পেশেণ্ট, যদি বেছে নিতেই হয় দুটোর মধ্যে একটা, কোনটা বাছবেন আপনি, ‘এ’ না ‘বি’?
২.
আদর্শ আর হরিপুর তো মনগড়া, যেমন মনগড়া বেকার-ক্রেমারের টেবিল, কিন্তু এর পরের উদাহরণ-টা আসল, মানে এক্কেবারে সাক্ষাৎ জর্নলের পাতা থেকে।
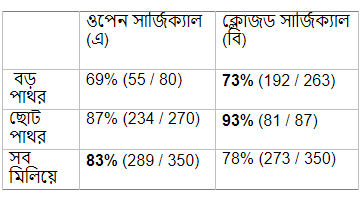
Charig et al. (1986) এর একটি বিখ্যাত পেপার২ থেকে কিডনি স্টোনের চিকিৎসার যে ডেটা পাওয়া যায়, সেও একদম এক ছাঁচ। দুটো সার্জিক্যাল চিকিৎসার একটি (“বি”) বড়ো পাথরের জন্যেও ভালো, ছোটোর জন্যেও, অথচ সব মিলিয়ে এগ্রিগেট করলে হিসেব উলটে যায়, দেখা যায় – ‘এ’-র সাফল্যের শতাংশ একটু হলেও বেশী।এই যে ডিগবাজি খাওয়ার প্যাটার্ণ-টা দেখলেন তিনটে উদাহরণে, রাশিবিজ্ঞানের ভাষায় এর-ই নাম “সিম্পসন’স প্যারাডক্স”১,৩। সহজে বললে, যেখানেই দেখা যায় যে অনেকগুলো গ্রূপে আলাদা করে একটি “ট্রেন্ড” দিব্যি স্পষ্ট (ট্রেণ্ডের বাংলা কি? ধারা?) কিন্তু গ্রূপটুপ জুড়ে দিলেই সে বেমালুম হাওয়া, সেইখানেই গ্রূপের আড়ালে উঁকি মারছেন সিম্পসন।
আসলে হচ্ছেটা কী তাহলে?
প্রোবাবিলিটির আঁক কষলে, বা আরও একধাপ এগিয়ে কজাল (causal) ইনফারেন্সের কায়দায় ডায়াগ্রাম ছবি এঁকে একটা ভীষ্মের শরশয্যার কার্টুন খাড়া করলে লোকে তেড়ে আসবেন তাই একটা সহজ ছবি দিয়েই একটু ব্যাখ্যা দিই নীচে।উপরের ছবিটা দেখুন। যদি শুধু নীল রঙের পয়েন্টগুলোকে সরলরেখায় জোড়েন, মনে হবে রেখার অভিমুখ উর্ধ্বে, মানে পজিটিভ ট্রেণ্ড, X বাড়লে Y-ও বাড়বে, আবার লাল রঙের বেলায়-ও তাই। কিন্তু কেউ যদি এসে লাল-নীল সব রঙ মুছে দেন – তাহলে যে সরল-রেখাটি এইবারে আঁকবেন (কালো ডট-ড্যাশ রেখাটি) সেইটি কিন্তু নিম্নগামী।
অর্থাৎ, সিম্পসনের ভাষায়, the trend reverses when groups are combined.
তাহলে কি সব-সময়েই এইরকম গ্রূপ জুড়ে দিলেই ট্রেন্ড পালটে যায়? অবশ্যই না।
হরিপুর আর আদর্শের টেবিল-টা আরেকবার দেখুন। হরিপুরে ২০% ছেলে, ৮০% মেয়ে, আর আদর্শে ঠিক তার উল্টো ! ওই এক-ই টেবিলে যদি হরিপুর আর আদর্শে ছেলে-মেয়ের পারসেন্টেজ না পাল্টাতো, তাহলেই আর অঙ্ক ওল্টাতো না। বিশ্বাস না হলে দুইদিকের পাল্লা সমান করে দেখুন, অঙ্ক মেলে কি না।
বেকারবাবুদের উদাহরণ, আর কিডনি-স্টোনের গল্প-ও তাই। বড়ো পাথরের জন্যে, যেগুলো হয়তো আরও জটিলতর সমস্যা, ডাক্তার-বাবুরা ট্রিটমেন্ট ‘এ’ বেশী ব্যবহার করেছেন, আর ছোটোর জন্যে ‘বি’। কাজেই ট্রিটমেন্ট ‘বি’ নিকৃষ্টতর হলেও, বেশী কঠিন কেসে কম ব্যবহৃত হওয়ার জন্যেই শতকরা হিসেবে এগিয়ে। আবার ‘এ’ হয়তো আসলেতে উন্নততর পদ্ধতি, কিন্তু তাকেও বেশীবার দিতে হচ্ছে কঠিন পরীক্ষা।
প্রথম উদাহরণে জেণ্ডার (লিঙ্গ) আর দ্বিতীয় উদাহরণে রোগের জটিলতা (সিভিয়ারিটি) – এদের রাশিবিজ্ঞানের ভাষায় বলা হয় “লার্কিং ভেরিয়েবল”, অর্থাৎ ঘাপটি মেরে বসে থাকা চলরাশি। এদের না ধরলেই হিসেব উলটে সে এক বিচ্ছিরি কাণ্ড !
৩.
শেষ করবো আরও দুটো উদাহরণ দিয়ে, যদিও আগের পর্বের মতন এইবারেও বলাটা অন্যায় হবে না যে চোখ মেলে চাইলে চাদ্দিকে বিস্তর প্রাঞ্জল উদাঃ দেখতে পাবেন।
প্রথমটা বার্কলি বিশ্ববিদ্যালয়ের – ১৯৭৩ সালে যাদের বিরুদ্ধে লিঙ্গবৈষম্যের অভিযোগ ওঠে। সেই বছরের গ্র্যাজুয়েট স্কুলে ভর্তির তথ্যে দেখা যায়, পুরুষ আবেদনকারীদের ৪৪% আর মহিলা আবেদনকারীদের ৩৫% উত্তীর্ণ, এবং ৪৪-৩৫ এর ব্যবধান নামমাত্র নয়। এই অভিযোগের ঠিক পরেপরেই ৭৫ সালে পিটার বিকেল ও তাঁর সহকর্মীরা একটি পেপারে৭ বার্কলির সবকটি ডিপার্টমেন্টের ভর্তির পরিসংখ্যান খতিয়ে দেখেন। আবার-ও সেই সিম্পসন’স প্যারাডক্স। দেখা যায় ৮৫-র মধ্যে ৬টি ডিপার্টমেন্টের বায়াস পুরুষদের বিপক্ষে, আর ৪টিতে মহিলাদের বিপক্ষে … এবং “examination of the disaggregated data reveals … about as many units appear to favor women as to favor men”. বিকেল-দের বক্তব্য ছিলো, এই উদাহরণটির লার্কিং ভেরিয়েবল ডিপার্ট্মেন্টগুলি কতোটা কম্পিটিটিভ সেই তথ্য। ওঁদের-ই অ্যাবস্ট্রাক্ট থেকেই সোজা চোতা করে দিই দুই লাইন, “The bias in the aggregated data stems not from any pattern of discrimination on the part of admissions committees, which seem quite fair on the whole, but apparently from prior screening at earlier levels of the educational system. Women are shunted by their socialization and education toward fields of graduate study that are generally more crowded, less productive of completed degrees, and less well funded, and that frequently offer poorer professional employment prospects.” (এইখানে বলে রাখা উচিত যে, শিক্ষা-ক্ষেত্রে লিঙ্গবৈষম্য আছে এবং ভয়ানকভাবেই আছে বলে মনে করি, বার্কলির এই উদাহরণ সেটাকে ডিস্প্রুভ করে না। এই বিষয় নিয়ে বলার অনেক কিছু থাকলেও এই পরিসরে সেই প্রসঙ্গ তুললাম না।)
শেষ করবো এমন একটা উদাহরণ দিয়ে যেটা আমাদের এই দুহাজার কুড়ি সালে এসে কান ধরে শিখিয়ে গেলো যে সিম্পসনের প্যারাডক্স যতোই বইয়ের পাতায় পড়ি, আসলে কিছুই মাথায় ঢোকেনি।
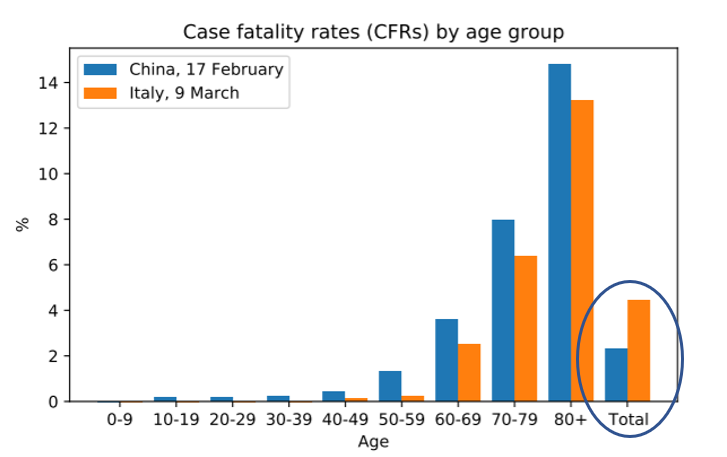
আর টেবিল নয়, বরং একটা ছবি দেখাবো। Kügelgen et al. দের পেপার৮ থেকে (মাপ করবেন বাংলা উচ্চারণ পারলাম না)।নিচের ছবিটি খেয়াল করে দেখুন। ইটালি আর চীনের, বয়েস অনুযায়ী, কেস ফেটালিটি রেট, অর্থাৎ কনফার্মড কেসের যত ভগ্নাংশ মারা গেছেন। পুরো প্লটে দেখা যাচ্ছে একদম ছোটো ০-৯ থেকে শুরু করে “৮০+” অব্দি প্রত্যেকটি এজ-গ্রূপেই চীনের CFR বেশি, অথচ যেই pool করলেন, উলটে গেলো - একদম ডানদিকে “টোটাল” ক্যাটেগরির দিকে তাকান, নীল বারের উচ্চতা কমলা-র থেকে কম।
কী করে হলো এরকম? আবার সেই হরিপুর-আদর্শ ইস্কুলে ফিরে যান। সেখানে যেমন দুটো ইস্কুলের ছেলেমেয়ের অনুপাত সমান ছিলো না। এইখানেও ইটালি ও চীনের বয়স-অনুসারে কোভিড-আক্রান্ত বিন্যাস আলাদা, সত্যি বলতে বেশ অনেকটাই আলাদা। চীনের বেশীর ভাগ আক্রান্ত ৩০-৬০ এর মধ্যে আর ইটালীর আক্রান্ত-দের সবাই প্রায় ৬০+। এই ছবিতে সেইটিই “লার্কিং ভেরিয়েবল”।
এক পাতা লিখবো ভেবে আপাততঃ চার-পাঁচ পাতার নামিয়ে দিয়েছি কাজেই এইখানেই ইতি টানলাম। সিম্পসন’স প্যারাডক্স এর গল্পের যদিও ইতি নেই, আদি আছে কি না সে-ও বলা শক্ত। এই লেখাটায় টেকনিক্যাল খুঁটিনাটি সব বাদ দিলাম, তবে নীচে রেফারেন্সের তিন-নম্বরে জুডিয়া পার্লের একটা আর্টিকেল পাবেন, ইচ্ছে হলে ওইটি পড়ে দেখতে পারেন।
সিম্পসন’স প্যারাডক্স ‘অমনিপ্রেজেন্ট’, কাজেই মোলাকাত তার সাথে হবেই, জানতে বা অজান্তে … তবে আশা এই যে, একবার গল্পের মত করে ব্যাপার-টা বুঝে নিলে তাকে দেখলে আঁতকে উঠবেন না। বরং একটা উদাহরণ মনে মনে গেঁতে নিন, কখন কোথায় চক-ডাস্টার হাতে জ্ঞানের গোঁসাই হয়ে ট্যান দিতে হবে কেউ বলতে পেরেছে?
রেফারেন্সঃ
১)E. H. Simpson, “The Interpretation of Interaction in Contingency Tables”, Journal of the Royal Statistical Society. Series B (Methodological) , 1951, Vol. 13, No. 2 (1951), pp. 238-241
২) Charig, C. R., Webb, D. R., Payne, S. R., & Wickham, J. E. (1986). Comparison of treatment of renal calculi by open surgery, percutaneous nephrolithotomy, and extracorporeal shockwave lithotripsy. British medical journal (Clinical research ed.), 292(6524), 879–882. https://doi.org/10.1136/bmj.292.6524.879
৩)Understanding Simpson’s Paradox, Judea Pearl, Technical report, https://ftp.cs.ucla.edu/pub/stat_ser/r414.pdf
৪)Understanding Simpson’s paradox using a graph, Andrew Gelman’s blog. https://statmodeling.stat.columbia.edu/2014/04/08/understanding-simpsons-paradox-using-graph/
৫)Stuart G. Baker and Barnett S. Kramer. “Good for Women, Good for Men, Bad for People: Simpson's Paradox and the Importance of Sex-Specific Analysis in Observational Studies” Journal of Women's Health & Gender-Based Medicine.Nov 2001.867-872. http://doi.org/10.1089/152460901753285769
৬)Wang, B., Wu, P., Kwan, B., Tu, X. M., & Feng, C. (2018). Simpson's Paradox: Examples. Shanghai archives of psychiatry, 30(2), 139–143. https://doi.org/10.11919/j.issn.1002-0829.218026
৭)P. J. Bickel, E. A. Hammel, J. W. O'Connell, “Sex Bias in Graduate Admissions: Data from Berkeley Measuring bias is harder than is usually assumed, and the evidence is sometimes contrary to expectation”. https://homepage.stat.uiowa.edu/~mbognar/1030/Bickel-Berkeley.pdf
৮)von Kügelgen, J., Gresele, L., & Schölkopf, B. (2020). Simpson's paradox in Covid-19 case fatality rates: a mediation analysis of age-related causal effects. arXiv preprint arXiv:2005.07180. https://arxiv.org/abs/2005.07180
পুনঃপ্রকাশ সম্পর্কিত নীতিঃ এই লেখাটি ছাপা, ডিজিটাল, দৃশ্য, শ্রাব্য, বা অন্য যেকোনো মাধ্যমে আংশিক বা সম্পূর্ণ ভাবে প্রতিলিপিকরণ বা অন্যত্র প্রকাশের জন্য গুরুচণ্ডা৯র অনুমতি বাধ্যতামূলক।প্রথম কিস্তি | দ্বিতীয় কিস্তি | তৃতীয় কিস্তি | চতুর্থ কিস্তি | পঞ্চম কিস্তি | ষষ্ঠ কিস্তি | সপ্তম কিস্তি | অষ্টম কিস্তি | সমষ্টি থেকে ব্যষ্টি | ভক্স পপুলি | দুই লেজান্ড্রর গল্প | বিষের ইতিহাস, ইতিহাসের বিষ - আরও পড়ুনরাধিকা ও আর্শোলা - যদুবাবুআরও পড়ুনব্লাড টেস্ট, প্রসিকিউটর’স ফ্যালাসি ও ওয়ান্ডার উওম্যানের ল্যাসো – এজলাসে Bayes-বাবু - যদুবাবুআরও পড়ুনমধুবাতা ঋতায়তে - শারদা মণ্ডলআরও পড়ুনমধুবাতা ঋতায়তে - শারদা মণ্ডলআরও পড়ুনএপিটাফ ও এনট্রপি - যদুবাবুআরও পড়ুনভোগবাদের প্যারাডক্স - পাপাঙ্গুলআরও পড়ুননতুন ঠিকানা - abhisek boseআরও পড়ুনপ্রকৃত উত্তরাধুনিক? - পাপাঙ্গুলআরও পড়ুনকী চলছে দেশ বিদেশে? - Sumit Royআরও পড়ুনমধুবাতা ঋতায়তে - শারদা মণ্ডলআরও পড়ুনচিড়িয়াখানার লোকটা - শর্মিষ্ঠাআরও পড়ুনহে চিরসারথি - গুরুচণ্ডা৯
- মতামত দিন
-
বিষয়বস্তু*:
- পাতা : ১২
 নিরমাল্লো | 220.158.***.*** | ১৮ এপ্রিল ২০২১ ০৮:৪৭104844
নিরমাল্লো | 220.158.***.*** | ১৮ এপ্রিল ২০২১ ০৮:৪৭104844লার্কিং ভ্যারিয়েবল কি করে কাজ করে সেটা আর একটু বুঝিয়ে বল। টোটাল পপুলেশানের মিনটাকে নর্মালাইজ করে তারপরে মডেলে ফিট করার মত কিছু কি?
 Ki dorkar | 223.186.***.*** | ১৮ এপ্রিল ২০২১ ০৮:৫৮104848
Ki dorkar | 223.186.***.*** | ১৮ এপ্রিল ২০২১ ০৮:৫৮104848বাহ বাহ
-
যদুবাবু | ১৮ এপ্রিল ২০২১ ০৯:০৯104850
লার্কিং ভেরিয়েবল কাজ করে লুকিয়ে থেকে - মানে ধর তুই দেখছিস যে এ আর বি-এর মধ্যে বেশ স্ট্রং কোরিলেশন আছে, কিন্তু খুঁজলে দেখা যাবে, এ আর বি এর মাঝে ঘাপটি মেরে 'সি' লুকিয়ে আছে। এ আর সি, এবং সি আর বি কোরিলেটেড, কিন্তু এ আর বি-এর মধ্যে সম্পর্ক-টা হয়তো সরাসরি নয়।
ছোটোবেলায় একটা এমন ট্রিভিয়াল উদাহরণ দেওয়া হতো যে বয়েস বাড়লে মাইনে বাড়ে, আবার রক্তচাপ-ও বাড়ে, তাই মাইনে আর রক্তচাপের মধ্যে বেশ হাই কোরিলেশন, কিন্তু তার মানে এই নয় যে মাইনে বাড়লেই রক্তচাপ বাড়ে। অনেক সিরিয়াস ভালো উদাহরণ-ও আছে। যেমন প্রথম সন্তানের তুলনায় দ্বিতীয় বা দ্বিতীয়ের তুলনায় তৃতীয়ের ডাউন সিনড্রোম দেখা দেওয়ার সম্ভাবনা বেশী - এখানে কনফাউন্ডিং বা লার্কিং ভেরিয়েবল হচ্ছে মেটারনাল এজ। আরও অনেক অনেক এমন আছে - সোশ্যাল সায়েন্সেও অনেক চমৎকার উদাহরণ আছে। আবার কি করে এদের ধরা যায়, ধরলে কি করতে হয় এইসব নিয়ে কজাল ইনফারেন্সে অনেক কায়দাকানুন আছে।
আর কখনো কখনো জানা যায় যে লার্কিং ভেরিয়েবল-টা কি, কখনো যায় না - সেটার পোষাকী নাম স্পিউরিয়াস কোরিলেশন - একগাদা উদাহরণ এখানে পাবিঃ https://tylervigen.com/page?page=1
-
যদুবাবু | ১৮ এপ্রিল ২০২১ ০৯:১০104851
@কি দরকারঃ ধন্যবাদ !! :)
-
 উজ্জ্বল | ১৮ এপ্রিল ২০২১ ১০:২৫104866
উজ্জ্বল | ১৮ এপ্রিল ২০২১ ১০:২৫104866 প্রচুর অঙ্ক ভীতি নিয়েও পড়লাম, অনেকটা বুঝলাম। যদু বাবুর মাইনে, বয়স ও রক্তচাপের উদাহরণটাও অসাধারণ। সবাইকে অশেষ
-
যদুবাবু | ১৮ এপ্রিল ২০২১ ১৯:৩৩104886
অনেক ধন্যবাদ, উজ্জ্বল ! 'লার্কিং ভেরিয়েবল' নিয়ে কোনো একটি সংখ্যায় গুছিয়ে লিখবো ইচ্ছে আছে।
আর অঙ্কভীতি তো সত্যি বলতে অঙ্কের মাস্টারমশাই হয়েও আমার এতো দিনেও কাটেনি, এক একদিন দুঃস্বপ্নে দেখেছি ক্লাসে একটা থিয়রেম প্রুফ করতে শুরু করে গুবলেট হয়ে গেছে আর পেছনে বাচ্চারা খুকখুক করে চাপা গলায় হাসছে।
-
Ramit Chatterjee | ১৮ এপ্রিল ২০২১ ২১:১২104890
যদু বাবুর টিউশনি দারুন ভাবে এনজয় করলাম। এই লারকিং ভেরিয়েবল ব্যাপারটা ভীষন ইন্টারেস্টিং লাগল। চালিয়ে যান, দারুন হচ্ছে।
 দু | 47.184.***.*** | ১৮ এপ্রিল ২০২১ ২১:৫৩104892
দু | 47.184.***.*** | ১৮ এপ্রিল ২০২১ ২১:৫৩104892খুব সুন্দর বুঝিয়ে ছেন ধন্যবাদ
 Abhyu | 47.39.***.*** | ১৮ এপ্রিল ২০২১ ২২:৩১104895
Abhyu | 47.39.***.*** | ১৮ এপ্রিল ২০২১ ২২:৩১104895এই ভাবেও ভাবা যায়, a/b is greater than x/y আর c/d is greater than z/w, কিন্তু তার মানে এই নয় যে (a+c)/(b+d) সব সময় (x+z)/(y+w)এর চেয়ে বড় হবে।
-
যদুবাবু | ১৯ এপ্রিল ২০২১ ০০:১৮104900
রমিত, দু - আপনাদের অনেক ধন্যবাদ ! টিউ-শনি বেশ ভালো নাম, শনিবারেই বেরিয়েচে যখন।
অভ্যু-দাঃ এইটাই আসলে এক লাইনে বলার মতো সিম্পসন'স প্যারাডক্স। লিখবো ভেবেও আবার কিন্তু কিন্তু করুলাম।
এই লেখাগুলো কী করলে ভালো হয় সেই নিয়ে তোমার উপদেশ নিতে চাই। আর যদি অন্য কোনো টপিক-এর সাজেশন দাও তা'লে তো খুব খুব ভালো।
আমার আপাততঃ ইচ্ছে আছে একটু ইন্ডিপেন্ডেন্স / কন্ডিশনাল প্রোবাবিলিটি নিয়ে লিখবো, একটু অন্যান্য ফ্যালাসি বা কাউণ্টার-ইনটুইটিভ উদাহরণ - বার্থডে বা ম্যাচিং প্রবলেম ইত্যাদি, 'র্যাণ্ডমনেস' বোঝা নিয়ে একটা, আর একটু অ্যালগোরিদমিক বায়াস।
 Abhyu | 198.137.***.*** | ১৯ এপ্রিল ২০২১ ০১:৫২104904
Abhyu | 198.137.***.*** | ১৯ এপ্রিল ২০২১ ০১:৫২104904জ্যোতিষ্ক অত্যন্ত গুণী ছেলে। শুধু রিসার্চেই নয়, লেখার হাতও অত্যন্ত ভালো। খুব সুন্দর করে সবার জন্যে বুঝিয়ে লিখতে পারে, সেটা সবার কর্ম নয়।
থিওরেম প্রুফ করা নিয়েও টেনশন কিছু নেই - সেই রামার ঘটনা লিখেছিলাম আইএসআইএর টইতে - কে কে রয় অনেক কাণ্ড করে তিনটে বোর্ড জুড়ে প্রুফ করার পরে রামা বলেছিল বাট স্যার দ্য প্রোব্যাবিলিটি অফ দ্য ইভেন্ট উইল বি হাফ এনিওয়ে।
প্রোব্যাবিলিটি নিয়ে লেখা বেশ ভালো আইডিয়া। এই গুরুতেই দেখেছি A given B আর B given Aর তফাৎ করতে না পেরে লোকজনকে পাতার পর পাতা তর্ক করে যেতে - জাস্ট কোনো কমেন্ট না করে মুচকি মুচকি হাসতাম তখন :)
 Abhyu | 198.137.***.*** | ১৯ এপ্রিল ২০২১ ০১:৫৯104905
Abhyu | 198.137.***.*** | ১৯ এপ্রিল ২০২১ ০১:৫৯104905জেসিকা হার্ভার্ডের একজন লিবার্যাল আর্টসের জুনিয়র স্টুডেন্ট, কবিতা লেখে, উইকেণ্ডে সমাজসেবার কাজ করে। আর তার রুমমেট হল লরেন, সেও হার্ভাডের জুনিয়র - একই সাথে হার্ভার্ড জয়েন করেছিল। ফার রাইট গ্রুপের বিরুদ্ধে একটা পিটিশনে সই করার চান্স কার বেশি?
যদুবাবুর মাস্টারমশাই এটা আমাদের ক্লাসে পড়িয়েছিলেন।
-
যদুবাবু | ১৯ এপ্রিল ২০২১ ০২:৫৬104906
কনজাংশন ফ্যালাসি ! দারুণ মনে করিয়ে দিলে !! জেকেজি ঠিক এই প্রশ্ন-টা আমাকে প্রথম দিন-ই মিটিং-এ জিগ্যেস করেছিলেন। (অবশ্য আমার যে আগে উত্তর-টা জানা ছিলো, সেটা আর বলিনি।)
এইটার একটা ব্যাখ্যা Kahnemann,Tversky-এর বইতেও পড়েছি, ওদের উদাহরণ-টা এইরকমঃ
"Linda is 31 years old, single, outspoken, and very bright. She majored in philosophy. As a student, she was deeply concerned with issues of discrimination and social justice, and also participated in anti-nuclear demonstrations. Which is more probable?- Linda is a bank teller.
- Linda is a bank teller and is active in the feminist movement."
ওদের উদাহরণ-গুলো নিয়ে দুর্ধর্ষ একটা লেখা হতে পারে, অবশ্য সবার পড়া কি না কে জানে?
-
যদুবাবু | ১৯ এপ্রিল ২০২১ ০৩:০৭104907
আগের কমেন্ট-টা মিস করে গেছি।
"A given B আর B given Aর তফাৎ করতে না পেরে" - এইটাই তো Prosecutor's fallacy, তাই না? প্রোবাবিলিটি অফ এভিডেন্স গিভেন ইনোসেন্স, আর ইনোসেন্স গিভেন এভিডেন্স গুলিয়ে ফেললেই বিপত্তি।
আমি এই বছর দুইতিন আগেই ক্লাসে বাচ্চাদের OJ Simpson trial এ এইটা কেমন ভুল হয়েছে বলছিলাম, আশ্চর্য হয়ে গেলাম দেখে যে এঁরা অনেকেই ওজে-র নাম জানে না। অবশ্য সেই বছর-ই একটা ডকু বেরোলো। তারপর দেখি সবাই জানে।
রামা-দার গল্পটা এখন লেজেন্ড-এর পর্যায়ে। ওঁর-ই এক যোগ্য জুনিয়র বছর কয়েক পরে অলোক গোস্বামী-কে প্রুফের মাঝপথে আটকে যেতে দেখে অম্লান বদনে বলেছিলো, 'ডোণ্ট টেক চাপ, টেক p = 1/2'. (টেক পি ইক্যুয়াল টু হাফ)।
 Abhyu | 198.137.***.*** | ১৯ এপ্রিল ২০২১ ০৩:০৮104908
Abhyu | 198.137.***.*** | ১৯ এপ্রিল ২০২১ ০৩:০৮104908JKG এটাই বলেছিলেন আমি একটু গণ্ডোগোল করে ফেলেছি :)
 Hanglaatherium | 116.193.***.*** | ১৯ এপ্রিল ২০২১ ২২:৩৬104924
Hanglaatherium | 116.193.***.*** | ১৯ এপ্রিল ২০২১ ২২:৩৬104924যদি কখনও কোনো dataset বিশ্লেষণ করে Simpson's paradox দেখা যায় তাহলে সেটা data কিভাবে বিশ্লেষণ করা হয়েছে সে ব্যাপারে এক জোরদার প্রশ্ন তোলে| দুই প্রতিদ্বন্দ্বী দেশ "ক" আর "খ" এর মেয়েদের গড় আয়ু আর ছেলেদের গড় আয়ু বিশ্লেষণ করলে যদি দুটো তেই "ক" দেশ টি এগিয়ে থাকে কিন্তু সমগ্র গড়ে যদি পিছিয়ে যায় তাহলে এটা ভাবা উচিত যে আমাদের কি আদৌ সমগ্র গড় করার কোনো মানে হয়? মেয়েদের গড় আয়ু আর ছেলেদের গড় আয়ু হয়তো শারীরিক তফাৎ থাকার কারণেই আলাদা| জোর করে সামগ্রিক গড় করলে সেই ফলাফলের কিছু স্পষ্ট interpretation থাকে না| যেমন আমি যদি আমার বয়সের সাথে আমার মাধ্যমিকের ফলাফল যোগ করে অন্যান্য দের সাথি এইটা তুলনা করি তার কোনো মানে দাঁড়ায় না|
-
যদুবাবু | ২০ এপ্রিল ২০২১ ০০:১৭104925
"আমাদের কি আদৌ সমগ্র গড় করার কোনো মানে হয়?" - সিম্পসন'স প্যারাডক্স ধরা পড়লে তো নয় বটেই। না হলে মিস-লিডিং একটা সিদ্ধান্তে পৌঁছে যাওয়ার ভয় থাকে। জুডেয়া পার্লের টেকনিক্যাল রিপোর্ট-টায় এই নিয়ে সুন্দর বুঝিয়েছেন।
তবে, "আমি যদি আমার বয়সের সাথে আমার মাধ্যমিকের ফলাফল যোগ করে" - সেখানে তো ভেরিয়েবলগুলো-ই আলাদা - ইউনিট আলাদা ইত্যাদি। সিম্পসন'স প্যারাডক্সের এই উপরের উদাহরণ-গুলোয় কিন্তু ভেরিয়েবল এক-ই, কিন্তু গড় নিলে ট্রেন্ড পালটে যেতেই পারে, কারণ ওই অভ্যুদা যা বললেন উপরে, অথবা লার্কিং ভেরিয়েবলের উপস্থিতি।
-
Ranjan Roy | ২০ এপ্রিল ২০২১ ০৭:২৬104929
যদু ও মধু দুজনকেই অনেক ধন্যবাদ। চমৎকার আলোচনা।
দুবছর আগে কোরসেরায় অনলাইনের একটা চার মডিউলের কোর্স করেছিলাম লজিক নিয়ে। তাতে কনজাংশন ও ডিসজাংশন ফ্যালাসি নিয়ে অনেক ট্রুথ টেবিল হোমটাস্ক করিয়েছে মনে পড়ছে। লিন্ডার উদাহরণ নাম বদলে ছিল।
সব ভুলে গেছি। তাই যদুবাবুর আগামী ক্লাসের ওর অপেক্ষায়।
 Abhyu | 47.39.***.*** | ২০ এপ্রিল ২০২১ ০৯:০৮104936
Abhyu | 47.39.***.*** | ২০ এপ্রিল ২০২১ ০৯:০৮104936রঞ্জনদা, লিন্ডার গল্পটা এরকম - প্রোব্যাবিলিটি অফ A ইজ গ্রেটার দ্যান প্রোব্যাবিলিটি অফ (A and B)। এখানে A হচ্ছে ব্যাঙ্ক টেলার আর B হচ্ছে ফেমিনিস্ট। প্রবলেমটা হচ্ছে আপনি মনে মনে ধরে নিচ্ছেন A আসলে (A and NOT B), তা তো নয় আসলে!
-
Ranjan Roy | ২০ এপ্রিল ২০২১ ১০:০৮104942
অ্যাই! ঠিক বলেছ। ওই মনে মনে ধরে নেওয়। ভুলে যাই-- যে রাঁধে সে চুল বাঁধে না, এমন মাথার দিব্যি কেউ দেয়নি। অর্থাৎ A, B not mutually exclusive, ।
এবং ( A and B)হল subset of A. কাজেই P(.A )> P ( A and B).
ঠিক বুয়েছি?
-
যদুবাবু | ২০ এপ্রিল ২০২১ ১৮:৪০104956
হ্যাঁ রঞ্জন-দা, একদম ঠিক বুঝেছেন ! লিণ্ডার গল্প-টা যে পেপারে ছিলো তার Abstract-এর প্রথম সেণ্টেন্স-ই ঐটা। ঐ যে রাঁধে সে চুল বাঁধবে না ধরে নেওয়া-টাকে ওঁরা বলেছিলেন "রিপ্রেজেন্টেটিভনেস"। দুটো বর্ণনা-র মধ্যে দ্বিতীয়-টা শুনে মনে হয় ওইটা লিণ্ডাকে বেশী "রিপ্রেজেন্ট" করে।
-
যদুবাবু | ২০ এপ্রিল ২০২১ ১৮:৪৭104957
পেপারের লিঙ্কঃ https://pages.ucsd.edu/~mckenzie/TverskyKahneman1983PsychRev.pdf
পরে দেখতে পারেন। দারুণ দারুণ এক্সপেরিমেন্ট আছে। একটা যেমন আমার পার্সোন্যাল ফেভারিটঃব্র্যাকেটের নম্বরগুলো র্যাঙ্ক (১ - হওয়ার চান্স সবথেকে বেশী, ২ - আরেকটু কম ইত্যাদি)। লোকে তিন নম্বর অপশন-টা (ফার্স্ট সেট খুইয়েও ম্যাচ বের করে নেবে)-টাকে বেশী প্রোবাবল মনে করে শুদ্ধু (ম্যাচ জিতবে) - এই ইভেন্ট-টার থেকে।
এইটা আমি বিয়ন বর্গের জায়গায় রজার ফেডারার বসিয়ে এক্সপেরিমেন্ট করে দেখেছি, খুব বেশী পাল্টায় না। :)
-
যদুবাবু | ২০ এপ্রিল ২০২১ ১৮:৫১104958
একটু বাজে ছড়িয়ে ফেলেছি তাড়াহুড়ো করতে গিয়ে।
"Borg will lose the first set but win the match"(C) is rated more likely than "Borg will lose the first set" (B).
-
Ranjan Roy | ২০ এপ্রিল ২০২১ ১৯:০৯104960
বুঝতে পারছি। Sample size= will lose the first set.
Subset= will lose the first set but win.
কিন্ত খুঁটিয়ে না দেখলে পরেরটা বড় মনে হবে।
-
Ranjan Roy | ২১ এপ্রিল ২০২১ ০০:৪০104965
আচ্ছা, জেসিকা এবং লরেন এর পিটিশন সাইন কেসে দুটোই ইন্ডিপেন্ডেন্ট ইভেন্ট তো? তাহলে দুটোরই 1/2 হওয়ার কথা।
ছড়িয়েছি?
 Abhyu | 198.137.***.*** | ২১ এপ্রিল ২০২১ ০১:২৫104967
Abhyu | 198.137.***.*** | ২১ এপ্রিল ২০২১ ০১:২৫104967জেসিকা লরেনটা ঠিক দেওয়া হয় নি।
A = হার্ভার্ডে ঐ বছর ভর্তি হওয়া মেয়ে
B = লিবার্যাল আর্টস, সমাজসেবা
C = সই
তাহলে একটা P(C given A) অন্যটা P(C given (A and B)) এই রকম আর কি।
-
Ranjan Roy | ২১ এপ্রিল ২০২১ ১০:৪৯104978
থেংকু অভ্যু
একদম কিলিয়ার।
আচ্ছা, ঘরে বসে প্রোবাবিলিটির আঁক করার, এলিমেন্টারি লেভেলের কোন বই সাজেস্ট করবে? একদম পি ফর ডাম্ব গোছের?
বৃটিশ কাউন্সিলের লাইব্রেরিতে একটা পাতলা পুরনো বই ছিল যাতে স্যাম্পল ডেটা নরমাল ডিস্ট্রিবিউশন হলে এরর লিমিট কেন দুদিকে 5% ধরা হয় সেটা ভাল করে বুঝিয়েছে--- ওরকম কোন বই।
-
যদুবাবু | ২১ এপ্রিল ২০২১ ১৭:৪৮104984
রঞ্জন-দা, আমার এক বন্ধুকে কয়েকদিন আগেই ঠিক এই প্রশ্নের উত্তর দিলাম। তাকে করা ইমেল-টাই আবার টুকে দিচ্ছি।
প্রথম-টা নতুন, ঐটা বাদ দিয়ে সব-কটাই পিডিএফ সার্চ করলেই পাওয়া যায় ইন্টারনেটে, আর সেটা আপত্তিকর হলে পড়ার বইয়ের দোকানেও খুঁজলে পাওয়া যেতে পারে।১। “Fundamentals of Probability: A First Course” by Anirban Dasgupta. (http://www.springer.com/us/book/9781441957795) [এইটি আমার ফার্স্ট ইয়ারের ছাত্রদের পড়ানোর টেক্সট। পড়ানোর জন্যেও ভালো আর অনির্বাণ-দা আমার শিক্ষক-ও বটে, ওনার pedagogy আমার সাথে মেলে। ].
২। A First Course in Probability: Sheldon Ross. [বিখ্যাত বই, সর্বত্রগামী, মাঝে মাঝে ইতিহাসের পাদটীকাও আছে, তবে একটু দামড়া, ব্লান্ট ইন্সট্রুমেন্ট অথবা আপৎকালীন বালিশ হিসেবেও ব্যবহার করা যায়।]
৩। Grinstead and Snell’s Introduction to Probability (পুরোনো টেক্সট, অতো না চললেও ফ্রি-তে পাওয়া যায় লেখক-দের সাইটে, তাই রেকমেণ্ড করিঃ https://math.dartmouth.edu/~prob/prob/prob.pdf )
৪। Introduction to Probability Theory – Hoel, Port & Stone. [বিখ্যাত বই, আকারে একটু কৃশকায়, তাই ভালো লাগে।]
৫। An Introduction to Probability Theory and Its Applications, William Feller (সর্বকালের সেরা বই এইটি, আমরা আই-এস-আই-এর ফার্স্ট-সেকেণ্ড ইয়ারে পড়েছি, একটু শক্ত লাগলেও অবিশ্বাস্য রকমের ভালো বই। আমার চেনা এক রাশান প্রোবাবিলিস্ট/লেখক বলেছিলেন তাকে যদি একটা নির্জন দ্বীপে পাঠানো হয় আর দুইটি মাত্র বই সঙ্গে রাখার অনুমতি দেওয়া হয়, তিনি কোনো কবিতা বা সাহিত্যের বই না নিয়ে শুধু ফেলারের দুই ভল্যুম নিয়ে পোঁছে যাবেন। অঙ্ক কষে আর ভেবে সময় কেটে যাবে।)
 Abhyu | 47.39.***.*** | ২১ এপ্রিল ২০২১ ১৭:৪৮104985
Abhyu | 47.39.***.*** | ২১ এপ্রিল ২০২১ ১৭:৪৮104985রঞ্জনদা, দেখুন তো এটা খুলতে পারেন কিনা https://mbapreponline.files.wordpress.com/2013/07/fifty_challenging_problems_in__2.pdf
হ্যাঁ বলেই দিচ্ছে চ্যালেঞ্জিং প্রবলেমস। তাতে কি? যদুবাবুকে যাদব চক্কোতি ভেবে প্রশ্ন করুন। ও জলের মতো সহজ করে বুঝিয়ে দিতে পারবে। বলতে মনে পড়ল, নরেন্দ্রপুরে গবা মহারাজের ঘরে অনুপ জলৌটার বিখ্যাত ভজনের ক্যাসেট বাজছে। আগেও অন্ততঃ হাজার বার বেজেছে।
- জলসে পাতলা কৌন হ্যায়?
সুরজিৎদা খট করে টেপ রেকর্ডার বন্ধ করে বললঃ
-তরুণদা বলুন তো জলসে পাতলা কৌন হ্যায়?
-জলের চেয়ে পাতলা? জলের চেয়ে ? (এক সেকেন্ড ভেবে) ইথার, ইথার...
 Abhyu | 47.39.***.*** | ২১ এপ্রিল ২০২১ ১৭:৫৫104987
Abhyu | 47.39.***.*** | ২১ এপ্রিল ২০২১ ১৭:৫৫104987যদুবাবু | ২১ এপ্রিল ২০২১ ১৭:৪৮
ফেলার? কি ভাগ্যি আমার প্যাট্রিক বিলিংসলি বলে নি :)
জোকস অ্যাপার্ট, ফেলারের মতো বই হয় না, তবে ওটা একটু কঠিন লাগতে পারে নিজে পড়ার জন্যে। হোয়েল পোর্ট স্টোনের বইটা আমার খুব পছন্দ। তবে প্রোব্যাবিলিটে আমি একেবারেই অনধিকারী, আমার বিদ্যে ঐ বেস থিওরেম পর্যন্ত আর জ্যোতিষ্কের পুরো কেরিয়ারটাই ঐ বেস থিওরেমের গাছপালা ফুল-ফল :)
- পাতা : ১২
- মতামত দিন
-
বিষয়বস্তু*:
-
গুরুচণ্ডা৯-র বই দত্তক নিন
কোনোরকম কর্পোরেট ফান্ডিং ছাড়া সম্পূর্ণরূপে জনতার শ্রম ও অর্থে পরিচালিত এই নন-প্রফিট এবং স্বাধীন উদ্যোগটিকে বাঁচিয়ে রাখতে এককালীন বা ধারাবাহিক ভাবে গুরুভার বহন করুন।
- ভাটিয়ালি | টইপত্তর | বুলবুলভাজা | হরিদাস পাল | খেরোর খাতা | বই
- বুলবুলভাজা : সর্বশেষ লেখাগুলি
(লিখছেন... )
(লিখছেন... )
(লিখছেন... বর্ণনা হালদার , হীরেন সিংহরায়, শিবাংশু)
(লিখছেন... Faruk Munshi, albert banerjee)
(লিখছেন... )
- হরিদাস পালেরা : যাঁরা সম্প্রতি লিখেছেন
(লিখছেন... )
(লিখছেন... অরিন, kk, অরিন)
(লিখছেন... )
(লিখছেন... অরিন, নীল, অরিন)
(লিখছেন... অরিন, হীরেন সিংহরায়, অরিন)
- টইপত্তর : সর্বশেষ লেখাগুলি
(লিখছেন... albert banerjee)
(লিখছেন... )
(লিখছেন... albert banerjee, দীপ, দীপ)
(লিখছেন... )
(লিখছেন... )
- কি, কেন, ইত্যাদি
- বাজার অর্থনীতির ধরাবাঁধা খাদ্য-খাদক সম্পর্কের বাইরে বেরিয়ে এসে এমন এক আস্তানা বানাব আমরা, যেখানে ক্রমশ: মুছে যাবে লেখক ও পাঠকের বিস্তীর্ণ ব্যবধান। পাঠকই লেখক হবে, মিডিয়ার জগতে থাকবেনা কোন ব্যকরণশিক্ষক, ক্লাসরুমে থাকবেনা মিডিয়ার মাস্টারমশাইয়ের জন্য কোন বিশেষ প্ল্যাটফর্ম। এসব আদৌ হবে কিনা, গুরুচণ্ডালি টিকবে কিনা, সে পরের কথা, কিন্তু দু পা ফেলে দেখতে দোষ কী? ... আরও ...
- আমাদের কথা
- আপনি কি কম্পিউটার স্যাভি? সারাদিন মেশিনের সামনে বসে থেকে আপনার ঘাড়ে পিঠে কি স্পন্ডেলাইটিস আর চোখে পুরু অ্যান্টিগ্লেয়ার হাইপাওয়ার চশমা? এন্টার মেরে মেরে ডান হাতের কড়ি আঙুলে কি কড়া পড়ে গেছে? আপনি কি অন্তর্জালের গোলকধাঁধায় পথ হারাইয়াছেন? সাইট থেকে সাইটান্তরে বাঁদরলাফ দিয়ে দিয়ে আপনি কি ক্লান্ত? বিরাট অঙ্কের টেলিফোন বিল কি জীবন থেকে সব সুখ কেড়ে নিচ্ছে? আপনার দুশ্চিন্তার দিন শেষ হল। ... আরও ...
- বুলবুলভাজা
- এ হল ক্ষমতাহীনের মিডিয়া। গাঁয়ে মানেনা আপনি মোড়ল যখন নিজের ঢাক নিজে পেটায়, তখন তাকেই বলে হরিদাস পালের বুলবুলভাজা। পড়তে থাকুন রোজরোজ। দু-পয়সা দিতে পারেন আপনিও, কারণ ক্ষমতাহীন মানেই অক্ষম নয়। বুলবুলভাজায় বাছাই করা সম্পাদিত লেখা প্রকাশিত হয়। এখানে লেখা দিতে হলে লেখাটি ইমেইল করুন, বা, গুরুচন্ডা৯ ব্লগ (হরিদাস পাল) বা অন্য কোথাও লেখা থাকলে সেই ওয়েব ঠিকানা পাঠান (ইমেইল ঠিকানা পাতার নীচে আছে), অনুমোদিত এবং সম্পাদিত হলে লেখা এখানে প্রকাশিত হবে। ... আরও ...
- হরিদাস পালেরা
- এটি একটি খোলা পাতা, যাকে আমরা ব্লগ বলে থাকি। গুরুচন্ডালির সম্পাদকমন্ডলীর হস্তক্ষেপ ছাড়াই, স্বীকৃত ব্যবহারকারীরা এখানে নিজের লেখা লিখতে পারেন। সেটি গুরুচন্ডালি সাইটে দেখা যাবে। খুলে ফেলুন আপনার নিজের বাংলা ব্লগ, হয়ে উঠুন একমেবাদ্বিতীয়ম হরিদাস পাল, এ সুযোগ পাবেন না আর, দেখে যান নিজের চোখে...... আরও ...
- টইপত্তর
- নতুন কোনো বই পড়ছেন? সদ্য দেখা কোনো সিনেমা নিয়ে আলোচনার জায়গা খুঁজছেন? নতুন কোনো অ্যালবাম কানে লেগে আছে এখনও? সবাইকে জানান। এখনই। ভালো লাগলে হাত খুলে প্রশংসা করুন। খারাপ লাগলে চুটিয়ে গাল দিন। জ্ঞানের কথা বলার হলে গুরুগম্ভীর প্রবন্ধ ফাঁদুন। হাসুন কাঁদুন তক্কো করুন। স্রেফ এই কারণেই এই সাইটে আছে আমাদের বিভাগ টইপত্তর। ... আরও ...
- ভাটিয়া৯
- যে যা খুশি লিখবেন৷ লিখবেন এবং পোস্ট করবেন৷ তৎক্ষণাৎ তা উঠে যাবে এই পাতায়৷ এখানে এডিটিং এর রক্তচক্ষু নেই, সেন্সরশিপের ঝামেলা নেই৷ এখানে কোনো ভান নেই, সাজিয়ে গুছিয়ে লেখা তৈরি করার কোনো ঝকমারি নেই৷ সাজানো বাগান নয়, আসুন তৈরি করি ফুল ফল ও বুনো আগাছায় ভরে থাকা এক নিজস্ব চারণভূমি৷ আসুন, গড়ে তুলি এক আড়ালহীন কমিউনিটি ... আরও ...
- টইপত্তর, ভাটিয়া৯, হরিদাস পাল(ব্লগ) এবং খেরোর খাতার লেখার বক্তব্য লেখকের নিজস্ব, গুরুচণ্ডা৯র কোন দায়িত্ব নেই। | ♦ : পঠিত সংখ্যাটি ১৩ই জানুয়ারি ২০২০ থেকে, লেখাটি যদি তার আগে লেখা হয়ে থাকে তাহলে এই সংখ্যাটি সঠিক পরিমাপ নয়। এই বিভ্রান্তির জন্য আমরা দুঃখিত।