The Death of Socrates - Jacques-Louis David , সূত্র
সোক্রাতিসের আগে
পিথাগোরাস
প্রাচীন ও বর্তমান পৃথিবীর ওপর যাঁর প্রভাব নিয়ে এই পরিচ্ছেদে আলোচনা করবো, সেই পিথাগোরাস (Pythagorus), বৌদ্ধিকভাবে, সর্বকালের সর্বাপেক্ষা গুরুত্বপূর্ণ ব্যক্তিদের একজন—যখন তিনি জ্ঞানী এবং তখনও, যখন তিনি অবিবেচক। প্রদর্শনধর্মী অবরোহী যুক্তি (deductive logic) হিসেবে অঙ্কের পথ চলা তাঁর হাতেই শুরু, আর তাঁর মাধ্যমেই এক অদ্ভুতুড়ে অতীন্দ্রিয়বাদের সঙ্গে যুক্ত। সেইজন্যে, দর্শনের ওপর অঙ্কের প্রভাব যে সেই সময় থেকেই একইসঙ্গে প্রগাঢ় এবং দুর্ভাগ্যজনক, তা কিছুটা তাঁর জন্যেই।

রোমের ক্যাপিটলাইন জাদুঘরে রাখা পিথাগোরাসের আবক্ষমূর্তি (সূত্র: উইকি)
তাঁর জীবন সম্পর্কে অল্প যেটুকু জানা আছে, তা দিয়েই শুরু করা যাক। সামিওস (Samos) দ্বীপের আদি বাসিন্দা পিথাগোরাসের উত্থানের সময়কাল আনুমানিক – ৫৩২ খ্রি.পূ.। কেউ বলেন তিনি এক প্রভাবশালী নাগরিক ম্নেসার্কোস (Mnesarchos)-এর সন্তান, কারুর মতে তিনি গ্রিক দেবতা অ্যাপোলো-র পুত্র; এর মধ্যে কোনটি ঠিক, তা নিজের পছন্দ অনুযায়ী বেছে নেওয়ার ভার আমি পাঠকের ওপরেই ছেড়ে দিলাম। তাঁর সময়ে সামিওস শাসন করতো স্বৈরাচারী পোলিক্রাতিস (Polycrates)—বেজায় ধনী আর এক বিরাট নৌবহরের মালিক।
সামিওস ছিল মাইলেটাস-এর বাণিজ্যিক প্রতিদ্বন্দ্বী; সামিওসের বণিকরা স্পেনের খনিজ-সমৃদ্ধ টার্টেসস অবধি ছড়িয়ে পড়েছিল। পোলিক্রাতিস সামিওসের একনায়ক হয় ৫৩৫ খ্রি.পূর্বে আর ৫১৫ খ্রি.পূ. পর্যন্ত তার শাসনকাল। বিবেক তাকে বিশেষ বিব্রত করেনি কখনও; যে দুই ভাই পোলিক্রাতিসকে তার শাসনকালের প্রথমদিকে স্বৈরাচার স্থাপনে সাহায্য করেছিল, প্রথম সুযোগেই পোলিক্রাতিস সেই কাঁটাদুটি সরিয়ে দেয় আর অন্যদিকে, তার নৌবহরের প্রাথমিক কাজ ছিল জলদস্যুতা। মাইলেটাস তার মাত্র কিছুদিন আগে পারস্যের বশ্যতা স্বীকার করেছিল আর সেইটে পোলিক্রাতিসের পক্ষে লাভজনক হয়। পশ্চিমদিকে পারস্যের আরও অগ্রগতি ঠেকাতে মিশরের রাজা আমাসিস-এর সঙ্গে সে মৈত্রী স্থাপন করে, কিন্তু পারস্য-সম্রাট কাম্বাইসিস যখন মিশর জয় করতে তাঁর পূর্ণশক্তি নিয়োগ করলেন, পোলিক্রাতিস বুঝতে পারে যে পারস্যের জয় অবশ্যম্ভাবী এবং অবিলম্বে দলবদল করে। নিজের রাজনৈতিক প্রতিপক্ষদের দিয়ে একটি নৌবহর সাজিয়ে সে মিশর দখল করতে পাঠায় [১]; সেই নৌসেনা বিদ্রোহ করে আর মাঝপথ থেকে ফিরে এসে সামিওস আক্রমণ করে। পোলিক্রাতিস এই আক্রমণ প্রতিহত করেছিল, কিন্তু শেষে নিজের অতি-লালসাই তার পতনের কারণ হয়। সার্দেস (বর্তমান কাতালোনিয়ায়)-এর সাত্রাপ (পারস্য প্রশাসনে রাজ্যপাল-এর তুল্য) তাকে বোঝায়, যে সে পারস্য-সম্রাটের বিরুদ্ধে বিদ্রোহ করতে ইচ্ছুক, আর পোলিক্রাতিসের সাহায্যের বিনিময়ে বিপুল ধনরাশি দিতে প্রস্তুত। এই প্রতারণায় বিশ্বাস করে পোলিক্রাতিস মূল ভূখণ্ডে এক বৈঠকে যোগ দিতে যায়, ধরা পড়ে ও ক্রুশবিদ্ধ হয়।

শলাপরামর্শরত পোলিক্রাতিস ও ফারাও আমাসিস (Der Ring des Polykrates, পোলিক্রাতিসের আঙটি নামক বইয়ের প্রচ্ছদ থেকে) (সূত্র: উইকি)
পোলিক্রাতিস কিন্তু একজন শিল্পের পৃষ্ঠপোষক ছিল। সর্বসাধারণের জন্যে বেশকিছু লক্ষ্যণীয় শিল্পকর্ম দিয়ে সে সামিওসকে সাজিয়েছিল। তার সভাকবি ছিলেন অ্যানাক্রেয়ন। তবে পিথাগোরাস তার শাসনপ্রণালী মোটেই পছন্দ করতেন না, আর তাই সামিওস ত্যাগ করেছিলেন। কথিত আছে—আর সম্ভবত সে কথা সত্যিও—পিথাগোরাস এরপর মিশরে যান আর তাঁর অধিকাংশ জ্ঞানার্জন সেখানেই হয়েছিল। সে যাই হোক, একটা কথা নিশ্চিত, যে তিনি শেষপর্যন্ত দক্ষিণ ইতালির ক্রোতন (Crotone, রাসেলের বানান Croton) শহরে থিতু হন।
দক্ষিণ ইতালির গ্রিক নগরগুলি সামিওস আর মাইলেটাসের মতোই সমৃদ্ধ ও সম্পদশালী ছিল; তদুপরি তাদের মাথায় সরাসরি পারসিক আক্রমণের খাঁড়াও ঝুলতো না [ক]। এদের মধ্যে সবচেয়ে প্রসিদ্ধ দুটি শহর ছিল সিবারিস আর ক্রোতন। বিলাসব্যসনে সিবারিসের খ্যাতি প্রবাদপ্রতিম; দিওদোরসের বক্তব্য – সমৃদ্ধির শীর্ষে থাকার সময়ে সিবারিসের জনসংখ্যা ছিল প্রায় তিন লক্ষ—যদিও এ নেহাতই অতিশয়োক্তি। ক্রোতনের আয়তনও প্রায় সিবারিস-এর সমানই ছিল। দুটি শহরেরই খরচ উঠতো আয়োনিয়া থেকে আমদানি করা সামগ্রী – কিছুটা ইতালির মধ্যে বিক্রি করে, বাকি পশ্চিম উপকূল দিয়ে গল (ফ্রান্সের আগের নাম) আর স্পেনে রপ্তানি করে। ইতালির গ্রিক নগরীগুলির মধ্যে ধুন্ধুমার লড়াই বেধেই থাকতো; পিথাগোরাস ক্রোতনে এসে পৌঁছনোর কিছুদিন আগেই তারা লক্রি-র কাছে পরাজিত হয়েছিল। তবে তাঁর আসার কিছু সময়ের মধ্যেই ক্রোতন সিবারিস-এর সঙ্গে এক যুদ্ধে পূর্ণ জয়লাভ করে – যাতে সিবারিস সম্পূর্ণ ধ্বংস হয়ে গিয়েছিল (৫১০ খ্রি.পূ.)। সিবারিস-এর সঙ্গে মাইলেটাস-এর ঘনিষ্ঠ যোগাযোগ ছিল। ক্রোতনের খ্যাতি ছিল চিকিৎসাবিদ্যায়। ক্রোতনের দিমোকিদিস প্রথমে পোলিক্রাতিস, পরে দারিয়ুস-এর চিকিৎসক হয়েছিলেন।
ক্রোতন শহরে পিথাগোরাস কিছুদিনের জন্যে তাঁর শিষ্যদের নিয়ে এক প্রভাবশালী সমাজ গঠন করেছিলেন, কিন্তু শেষ অবধি শহরের বাসিন্দারা তাঁর বিরোধী হয়ে ওঠে আর তাঁকে দক্ষিণ ইতালিরই আরেক শহর মেতাপঁতিওনে চলে যেতে হয়; আমৃত্যু তিনি সেখানেই ছিলেন। কিছুকালের মধ্যেই তাঁর খ্যাতি কিংবদন্তীসুলভ হয়ে ওঠে, তাঁর অলৌকিক আর যাদুকরী শক্তির কথা ছড়িয়ে পড়ে, কিন্তু অন্যদিকে তিনি অঙ্কবিদদের এক গোষ্ঠীও স্থাপন করেছিলেন [খ]। এইভাবে দুই বিপরীতধর্মী বিবদমান ঐতিহ্য তাঁর জীবন-স্মৃতিকে ঘোলাটে করে তুলেছিল, যার জট ছাড়িয়ে সত্যের উন্মোচন করা এখন কঠিন হয়ে দাঁড়িয়েছে।
ইতিহাসের এক অন্যতম আকর্ষণীয় আর গোলমেলে চরিত্র এই পিথাগোরাস। তাঁকে ঘিরে গড়ে ওঠা ঐতিহ্য যে শুধু সত্যি-মিথ্যের এক অবিচ্ছেদ্য মিশেল তা-ই নয়, সেই সব গল্পের একেবারে সরল, সবচেয়ে কম বিভ্রান্তিকর সংস্করণের থেকেও এক অদ্ভুত মনোবৃত্তির পরিচয় ভেসে ওঠে। খুব সংক্ষেপে বলতে হলে, পিথাগোরাস যেন আইনস্টাইন আর শ্রীমতি এডি-র (অনুবাদক: বর্তমানের প্রাসঙ্গিক উদাহরণে বুঝতে চাইলে ‘সদগুরু’ ভেবে নিন) এক মিশ্রণ। তিনি এক ধর্ম প্রচার করতেন, যার মূল দুটি বক্তব্য হল – আত্মার পুনর্জন্ম হয় [গ] আর বরবটি (beans, অর্থাৎ রাজমা, শিম – সবই) খাওয়া পাপ। এই ধর্মমতটি অবশেষে এক ধর্মীয় সম্প্রদায়ের রূপ নেয়, যারা খাপছাড়াভাবে বিভিন্ন জায়গায় সরকারের দখল নিয়ে ‘পণ্ডিতদের শাসন’-এর পত্তন করেছিল, কিন্তু ‘অসংস্কৃত জনগড্ডল’ বরবটি খাওয়ার লোভ ত্যাগ করতে না পেরে অচিরেই বিদ্রোহ করে।
পিথাগোরীয় শাস্ত্রের কিছু নীতি হল:
১) বরবটি খাওয়া থেকে বিরত থাকতে হবে
২) মাটিতে পড়ে যাওয়া জিনিস তোলা যাবে না
৩) সাদা মোরগ ছোঁওয়া যাবে না
৪) রুটি টুকরো করা যাবে না
৫) অনুভূমিক কোনো দণ্ড ডিঙোনো যাবে না
৬) লোহা দিয়ে আগুন খোঁচানো যাবে না
৭) গোটা রুটি থেকে সরাসরি খাওয়া যাবে না
৮) মালা থেকে ফুল ছেঁড়া যাবে না
৯) কোয়ার্ট (এক গ্যালনের এক চতুর্থাংশ) মাপার পাত্রের ওপর বসা যাবে না
১০) প্রাণীর হৃদযন্ত্র ভক্ষণ করা যাবে না
১১) বড় রাস্তা দিয়ে হাঁটা যাবে না
১২) বাড়ির ছাদে চড়ুইয়ের বাসা হতে দেওয়া যাবে না
১৩) আগুন থেকে পাত্র সরিয়ে নেওয়ার পর ছাইয়ের ওপর সেই পাত্রের ছাপ রেখে দেওয়া যাবে না, ঘেঁটে দিতে হবে
১৪) আলোক-উৎসের পাশে রাখা আয়নায় মুখ দেখা যাবে না
১৫) ঘুম থেকে ওঠার পর বিছানা এমনভাবে গুটিয়ে রাখতে হবে, যাতে তাতে শরীরের ছাপ না থাকে। [ঘ]
এই আপাত-নীতিবাক্যগুলি সবই আসলে আদিম শাস্ত্র-নিষেধাজ্ঞা।

ষোড়শ শতকের শুরুর দিকের এক ফরাসি পাণ্ডুলিপিতে আঁকা পিথাগোরাস মটর গাছের থেকে বিতৃষ্ণায় মুখ ফিরিয়ে নিচ্ছেন (সূত্র: উইকি)
কর্নফোর্ড-এর মতে (From Religion to Philosophy), “বিজ্ঞানমনস্কতার বিপরীতে আমরা যে অতিলৌকিক রহস্যময়তাকে বসাই, পিথাগোরাস-এর অনুগামী-দল তার মূল স্রোতটির প্রতিনিধি।” পার্মেনিদিস (Parmenides)—যিনি তাঁর মতে ‘যুক্তির জনক’—সম্পর্কে তাঁর মত, যে তিনি “পিথাগোরিয়ানিজ়ম (Pythagoreanism, পিথাগোরীয়বাদ)-এরই এক প্রশাখাজাত এবং স্বয়ং প্লেটো ইতালীয় দর্শনে তাঁর নিজের অনুপ্রেরণা খুঁজে পেয়েছিলেন।” কর্নফোর্ড বলছেন – পিথাগোরিয়ানিজ়ম আসলে অর্ফিজ়মের এক সংস্কার আন্দোলন, ঠিক যেমন অর্ফিজ়ম ছিল দিওনিসুস-এর উপাসনার এক সংস্কার। ইতিহাস জুড়ে চলা যুক্তিবাদ আর অতীন্দ্রিয়বাদের এই পারস্পরিক বিরোধিতার প্রথম নিদর্শন গ্রিকদের মধ্যে দেখা দেয় – অলিম্পাসের দেবকূল বনাম অপেক্ষাকৃত কম সভ্য, আদিম বিশ্বাসগুলির একটু বেশি পক্ষপাতদুষ্ট (নৃতত্ত্ববিদদের মতে) দেবতারা। এই দ্বৈরথে পিথাগোরাস ছিলেন অতীন্দ্রিয়বাদের পক্ষে, যদিও তাঁর অতীন্দ্রিয়বাদের ধরন—অদ্ভুত হলেও—বৌদ্ধিক। নিজেকে তিনি এক আধা-দৈব চরিত্র মনে করতেন, আর নাকি বলেছিলেন: “আছে মানব, আছে দেব, আর আছে পিথাগোরাস।” তাঁর থেকে অনুপ্রাণিত সমস্ত সিস্টেমই, কর্নফোর্ডের মতে, “যেন অন্য জগতের, যেখানে ঈশ্বরের অদ্বিতীয় অস্তিত্বের তুলনায় দৃশ্য জগত মিথ্যা, মায়াময়—এক অশান্ত মাধ্যম—যেখানে কুয়াশা আর অন্ধকার, ঐশ্বরিক আলোক-রেখাকে টুকরো করে, আচ্ছন্ন করে।”
দিকেইয়ার্খোস (Dikaiarchos, অন্য বানান: Dicaearchus) বলছেন, যে পিথাগোরাস শেখাতেন: “প্রথমত আত্মা অমর, আর তা বিভিন্ন জীবে রূপান্তরিত হয়; তাছাড়াও, যা কিছু জন্মায়, তার পুনর্জন্ম হয় চক্রাকারে, এক বিশেষ আবর্তনের নিয়ম মেনে – কোনো প্রাণই নতুন নয়; সবশেষে, যা কিছুর জন্ম হয়, তাকে নিজের আত্মীয় বলে মনে করা উচিত।” [ঙ] কথিত আছে, সন্ত ফ্রান্সিস-এর মতোই পিথাগোরাস নাকি না-মানুষদের কাছেও নিজের বাণী প্রচার করতেন।
তাঁর প্রতিষ্ঠিত সমাজে পুরুষ ও নারীরা একইরকম অধিকার নিয়ে ভর্তি হতেন; সম্পত্তির অধিকার সর্বজনীন ছিল, প্রাত্যহিক জীবনধারণও ছিল সহজ, গোষ্ঠীবদ্ধ। বিজ্ঞান বা গণিতের আবিষ্কারকেও সকলের—এবং এক অতীন্দ্রিয় উপায়ে, এমনকি মৃত্যুর পরেও, পিথাগোরাসের—কৃতিত্ব বলে মনে করা হত। মেতাপঁতিওন শহরের ইপাসোস (Hippasus of Metapontum, রাসেলের বানান Hippasos of Metapontion) এই নিয়মের লঙ্ঘন করেছিলেন আর সেই পাপের দৈবী শাস্তি হিসেবে জাহাজডুবি হয়ে মারা যান।

১৯১৩ সালের এক ছবিতে আঁকা পিথাগোরাস মেয়েদের উদ্দেশে বক্তৃতা দিচ্ছেন (সূত্র: উইকি)
কিন্তু এ সবের সঙ্গে অঙ্কের সম্পর্ক কোথায়? সম্পর্ক এমন এক নীতির মাধ্যমে, যা অধ্যয়ন আর ধ্যানপরায়ণ এক জীবনযাপনের কথা বলে। বার্নেট গুছিয়ে বলছেন:
“এ জগতে আমরা বহিরাগত আর আমাদের আত্মার মন্দির এই দেহ, তবু আত্মহননের মাধ্যমে আত্মার মুক্তি কখনোই আমাদের পথ নয়; কারণ আমরা ঈশ্বরের সম্পত্তি, তিনিই আমাদের রাখাল আর তাঁর অনুমতি ব্যতিরেকে আমাদের পালানোর কোনো অধিকার নেই। অলিম্পিক খেলায় যেমন তিন ধরনের ক্রীড়াবিদ অংশগ্রহণ করেন, তেমনই এ জগতেও তিন রকমের মানুষ বর্তমান। সর্বনিম্ন শ্রেণীতে আছে তারা—যারা বেচাকেনার জন্যেই ধরায় এসেছে, আর তাদের ওপরে তারা—যাদের কাজ প্রতিদ্বন্দ্বিতা করা। সর্বশ্রেষ্ঠ তারাই—যারা শুধু পর্যবেক্ষণ করতে এসেছে। উদাসীন বিজ্ঞানচর্চাই অতএব সর্বশ্রেষ্ঠ জীবনযাপন আর যে সত্যিকারের দার্শনিক নিজেকে সেই কাজে নিয়োজিত করেন, তিনিই ‘জন্ম-চক্র’ থেকে সফলভাবে মুক্তিলাভ করেন।” [চ]
শব্দের অর্থের পরিবর্তন খেয়াল করলে তা থেকে অনেক কিছু শেখা যায়। এর আগে আমি ‘orgy’ শব্দটি নিয়ে আলোচনা করেছিলাম; এবারে ‘theory’ শদটিকে খেয়াল করা যাক। শব্দটির ব্যুৎপত্তি অর্ফীয়, কর্নফোর্ড যার মানে করেছেন ‘উদ্দীপ্ত সমবেদী মনোনিবেশ’ (passionate sympathetic contemplation)। তিনি বলছেন, এই অবস্থায় “দর্শক নিজেকে পীড়িত ঈশ্বরের সঙ্গে এক বলে ভাবে, তাঁর সঙ্গেই মৃত্যুবরণ করে আবার তাঁর নবজন্মের সঙ্গেই পুনরুত্থিত হয়।” পিথাগোরাসের ক্ষেত্রে এই ‘উদ্দীপ্ত সমবেদী ধ্যান’ ছিল বৌদ্ধিক, আর গাণিতিক জ্ঞানের উৎসমুখ। এইভাবে পিথাগোরীয়বাদের মাধ্যমেই 'থিয়োরি' শব্দটি তার বর্তমান অর্থ লাভ করে; কিন্তু পিথাগোরাস যাঁদের অনুপ্রাণিত করেছিলেন, তাঁদের সকলের কাছেই এর সঙ্গে এক ছটাক 'দিব্য-পরমানন্দ' মিশে ছিল। ইশকুলে যারা নিমরাজি হয়ে অল্পস্বল্প অঙ্ক শিখেছে, তাদের কাছে এ এক আশ্চর্য ব্যাপার বলে মনে হতে পারে; কিন্তু যারা অঙ্ক ভালোবাসে, কদাচিৎ হঠাৎ কোনো বিষয় বুঝতে পারার আনন্দ পায় অঙ্ক কষতে কষতে, পিথাগোরীয় ধারণা—ভুল হলেও—তাদের স্বাভাবিক বলেই মনে হবে। মনে হতে পারে, একজন প্রায়োগিক দার্শনিক তাঁর বস্তুজগতের খাঁচায় আবদ্ধ, কিন্তু এক বিশুদ্ধ গণিতের চর্চাকারী, একজন সঙ্গীতজ্ঞের মতোই, নিজের খেয়ালে তৈরি এক শৃঙ্খলাবদ্ধ জগতের স্রষ্টা।
বার্নেটের বিবরণে পিথাগোরীয় নৈতিকতার সঙ্গে আধুনিক মূল্যবোধের বিরোধিতা খেয়াল করার মতো। আধুনিক মানুষ ফুটবল খেলা দেখার সময় সাধারণ দর্শকের থেকে খেলোয়াড়দের মহত্তর বলে মনে করে। একইভাবে, রাষ্ট্রের ক্ষেত্রে খেলোয়াড়দের—অর্থাৎ রাজনীতিবিদদের—তারা সাধারণ দর্শকের চেয়ে মহান বলে মনে করে। মূল্যবোধের এই পরিবর্তন সমাজব্যবস্থার পরিবর্তনের সঙ্গে জড়িত – মহারথী, বাবু, অমিত বিত্তশালী, স্বৈরাচারী – সকলেরই শুভ ও সত্যের স্বরূপ সম্পর্কে নিজস্ব ধারণা আছে। গ্রিক মণীষার সঙ্গে জড়িয়ে থাকায়, বাবু-রা, দার্শনিক তত্ত্বের মাঠে এক লম্বা ইনিংস খেলে ফেলেছেন, কারণ, একদিকে ধর্মতাত্ত্বিকরা যেমন ধ্যান/মনোনিবেশের মহিমা কীর্তন করেছেন, অন্যদিকে নির্লিপ্ত সত্যানুসন্ধান অ্যাকাডেমিক জীবনদর্শনকে মর্যাদা দিয়েছে। বাবু তাঁরাই, যাঁরা নিজের সমান প্রতিষ্ঠার মানুষ দিয়ে তৈরি এক দলের সদস্য—যে দল দাসশ্রমের ওপর নির্ভর করে বেঁচে থাকে (অন্তত তাদের শ্রমের ওপর, যারা প্রশ্নাতীতভাবে এই ভদ্রলোকদের থেকে নিকৃষ্ট)। খেয়াল করা দরকার – যতক্ষণ জীবনে শ্রমের চেয়ে ধ্যানের পরিমাণ বেশি, ততক্ষণ বাবুয়ানার এই সংজ্ঞার মধ্যে সাধু-সন্তরাও পড়েন। সত্যের আধুনিক ধারণাগুলি—যার মধ্যে বাস্তববাদ আর যন্ত্রনির্ভরতাও পড়ে—তা বাবুয়ানি থেকে নয়, শিল্পায়নের থেকে এসেছিল।
দাসপ্রথার প্রতি সহনশীল সমাজব্যবস্থা নিয়ে আমরা যতই খারাপ ভাবি না কেন, বিশুদ্ধ গণিতের জন্যে আমরা উপরোক্ত বাবুদের প্রতি ঋণী। বিশুদ্ধ গণিতের সৃষ্টি হওয়ার ফলে ধ্যানের এই আদর্শ নিয়ে আরও বেশি কাজকর্ম হয়েছিল; এর ফলে এই আদর্শের দর বাড়ে— ধর্মতত্ত্বে, নীতিশাস্ত্রে আর দর্শনে নইলে তার এই সাফল্য পাওয়া হত না। পিথাগোরাসের দ্বৈতসত্তার—একাধারে ধর্মগুরু আর বিশুদ্ধ গণিতজ্ঞ—এই হল মোটের ওপর ব্যাখ্যা। দুই রূপেই তাঁর প্রভাব অপরিমেয়, আর আধুনিক মননে যতটা মনে হয়, দুইয়ের মধ্যে ততটা বিরোধও নেই।
জন্মলগ্নে, বিজ্ঞানের সব শাখার সঙ্গেই কোনো এক ধরনের ভ্রান্ত বিশ্বাস জড়িয়ে ছিল, যার ফলে সেই বিশ্বাসগুলির ওপর এক কল্পিত গুরুত্ব আরোপ করা হয়েছিল। জ্যোতির্বিদ্যার সঙ্গে জড়িয়েছিল জ্যোতিষশাস্ত্র, রসায়নের সঙ্গে অ্যালকেমি। অঙ্কের সঙ্গে যুক্ত ছিল এক আরও সূক্ষ্ম ধরনের ভ্রান্তি। গণিতের জ্ঞানকে আপাতভাবে নিশ্চিত, নিখুঁত আর সরাসরি বাস্তবে প্রয়োগযোগ্য মনে করা হত; তার চেয়েও বড় কথা, এই জ্ঞান শুধুমাত্র চিন্তা করেই লাভ করা সম্ভব ছিল—পর্যবেক্ষণের কোনো বালাই ছিল না এতে। ফলস্বরূপ, ধরে নেওয়া হল, গণিত এমন এক আদর্শের কথা বলে – দৈনন্দিন অভিজ্ঞতা যাকে ছুঁয়ে উঠতে পারে না। গণিতের ওপর এই বিশ্বাসের ওপর ভিত্তি করেই – ইন্দ্রিয়ের তুলনায় চিন্তাকে, পর্যবেক্ষণের তুলনায় অন্তর্দৃষ্টিকে বেশি গুরুত্ব দেওয়া হল। ইন্দ্রিয়গ্রাহ্য জগৎ যদি গণিতের ছাঁচে না বসে, তাতে যেন ইন্দ্রিয়গ্রাহ্য জগতেরই ক্ষতি। নানাভাবে এমন সব পদ্ধতির শরণাপন্ন হওয়া হল, যাতে গণিতজ্ঞের প্রদর্শিত আদর্শে পৌঁছনোর চেষ্টা করা যায়, আর এই চেষ্টা করতে গিয়ে যে ধরনের পরামর্শ দেওয়া হত – তা থেকেই জ্ঞানতত্ত্ব আর অধিবিদ্যার নানাবিধ সমস্যার সূত্রপাত। এই ধরনের দর্শনের শুরুই হয় পিথাগোরাসের হাত ধরে।

পঞ্চদশ শতকের কাঠখোদাই। পিথাগোরাস ঘণ্টা থেকে তারযন্ত্র - সবকিছুর টিউনিং ঠিক করছেন। (সূত্র: উইকি)
সকলেই জানেন – পিথাগোরাস বলেছিলেন, “সমস্ত কিছুই আসলে সংখ্যা”। আধুনিক মননে এই বক্তব্যটি নেহাত প্রলাপ বলে মনে হলেও, তিনি আসলে যা বোঝাতে চেয়েছিলেন – তা কিন্তু প্রলাপ ছিল না। তিনি সঙ্গীতে সংখ্যার গুরুত্ব আবিষ্কার করেছিলেন আর পাটীগণিতের সঙ্গে সঙ্গীতের যে সম্পর্ক তিনি স্থাপন করেছিলেন, ‘হার্মনিক গড়’ (harmonic mean) বা ‘হার্মনিক প্রগতি’ (harmonic progression)-র মতো গাণিতিক শব্দবন্ধগুলির মধ্যে দিয়ে তা আজও বেঁচে আছে। সংখ্যাকে তিনি আকার হিসেবে ভাবতেন, যেমনটা আমরা তাসের পাতায় বা ছক্কার গায়ে দেখতে পাই। এখনো আমরা সংখ্যার ‘স্কোয়্যার’ (square, বর্গ, যেমন 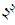 , আবার বর্গক্ষেত্রও বটে) ‘কিউব’ (ঘন, যেমন
, আবার বর্গক্ষেত্রও বটে) ‘কিউব’ (ঘন, যেমন 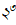 , আবার ঘনক-ও) নিয়ে কথা বলি, যে শব্দগুলির জন্যে আমরা তাঁর কাছে ঋণী। তিনি আয়ত-বৃত্তাকার/ডিম্বাকৃতি (oblong), ত্রিভুজাকৃতি, বা পিরামিডাকৃতি সংখ্যার কথাও বলেছিলেন। কোনো একটি আকৃতি তৈরি করতে যতগুলি নুড়ি-পাথর (আমরা কড়ি-ও ভাবতে পারি) লাগে, আকৃতিটি সেই সংখ্যার সঙ্গে যুক্ত। সম্ভবত তিনি জগতের এক পারমাণবিক ছবিতে বিশ্বাস করতেন, যেখানে পরমাণুগুলি নানা আকৃতিতে জুড়ে জুড়ে পদার্থের অণুগুলির গঠন করে। তাঁর আশা ছিল, এইভাবেই পাটীগণিত – পদার্থবিদ্যা তথা নন্দনতত্ত্বেরও অপরিহার্য পাঠ হয়ে উঠবে।
, আবার ঘনক-ও) নিয়ে কথা বলি, যে শব্দগুলির জন্যে আমরা তাঁর কাছে ঋণী। তিনি আয়ত-বৃত্তাকার/ডিম্বাকৃতি (oblong), ত্রিভুজাকৃতি, বা পিরামিডাকৃতি সংখ্যার কথাও বলেছিলেন। কোনো একটি আকৃতি তৈরি করতে যতগুলি নুড়ি-পাথর (আমরা কড়ি-ও ভাবতে পারি) লাগে, আকৃতিটি সেই সংখ্যার সঙ্গে যুক্ত। সম্ভবত তিনি জগতের এক পারমাণবিক ছবিতে বিশ্বাস করতেন, যেখানে পরমাণুগুলি নানা আকৃতিতে জুড়ে জুড়ে পদার্থের অণুগুলির গঠন করে। তাঁর আশা ছিল, এইভাবেই পাটীগণিত – পদার্থবিদ্যা তথা নন্দনতত্ত্বেরও অপরিহার্য পাঠ হয়ে উঠবে।
পিথাগোরাস অথবা তাঁর অব্যবহিত পরের শিষ্যদের মহত্তম আবিষ্কার সমকোণী ত্রিভুজের সেই উপপাদ্যটি, যার বয়ান হল, সমকোণের দুপাশের দুই বাহুর বর্গের যোগফল অপর বাহু বা অতিভুজের বর্গের সমান। মিশরীয়রা আগেই জানতেন যে, কোনো ত্রিভুজের বাহুগুলির দৈর্ঘ্য যথাক্রমে ৩, ৪ আর ৫ হলে তা সমকোণী ত্রিভুজ হয়, কিন্তু গ্রিকরাই সম্ভবত প্রথম দেখায় যে 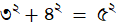 , আর এই আন্দাজ থেকেই সাধারণ নিয়মটির এক প্রমাণ আবিষ্কার করেন।
, আর এই আন্দাজ থেকেই সাধারণ নিয়মটির এক প্রমাণ আবিষ্কার করেন।

অ্যানিমেশনে পিথাগোরাসের উপপাদ্যের প্রমাণ (সূত্র: উইকি)
পিথাগোরাসের দুর্ভাগ্য, তাঁর উপপাদ্যটি থেকে সরাসরি অসমগুণনীয়ক (incommensurable, যাদের অনুপাত একটি অমূলদ (irrational) সংখ্যা, যেমন (√৩ এবং ২) সংখ্যা খুঁজে পাওয়া যায়, যা তাঁর পুরো দর্শনটিকেই নাকচ করে। একটি সমকোণী সমদ্বিবাহু ত্রিভুজের অতিভুজের বর্গ অন্য যে কোনো একটি বাহুর বর্গের দ্বিগুণ। এই সমান বাহুগুলির দৈর্ঘ্য যদি এক ইঞ্চি ধরে নিই, অতিভুজের দৈর্ঘ্য তবে কত? ধরা যাক, অতিভুজটির দৈর্ঘ্য ক/খ ইঞ্চি, তাহলে 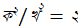 । ক এবং খ-এর গ.সা.গু দিয়ে দুই রাশিকেই ভাগ করলে যা পড়ে থাকে, তার একটি তবে অবশ্যই বিজোড় (দুটি-ই জোড় হলে তার ২ তবে গ.সা.গু-র মধ্যে চলে যায়)। যেহেতু
। ক এবং খ-এর গ.সা.গু দিয়ে দুই রাশিকেই ভাগ করলে যা পড়ে থাকে, তার একটি তবে অবশ্যই বিজোড় (দুটি-ই জোড় হলে তার ২ তবে গ.সা.গু-র মধ্যে চলে যায়)। যেহেতু 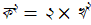 , অর্থাৎ ক জোড় সংখ্যা, খ নিশ্চয়ই তবে বিজোড়। এবার
, অর্থাৎ ক জোড় সংখ্যা, খ নিশ্চয়ই তবে বিজোড়। এবার 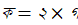 ধরলে,
ধরলে, 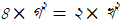 , অতএব
, অতএব 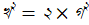 , মানে খ জোড়সংখ্যা – মূল প্রতিপাদ্যটি ভুল প্রমাণিত হল। তাহলে এমন কোনো ভগ্নাংশ ক/খ পাওয়া সম্ভবই না, যা দিয়ে অতিভুজটিকে প্রকাশ করা যায়। ইউক্লিডের জ্যামিতি বইয়ের দশম পর্বে এই প্রমাণটিই আছে [ছ]।
, মানে খ জোড়সংখ্যা – মূল প্রতিপাদ্যটি ভুল প্রমাণিত হল। তাহলে এমন কোনো ভগ্নাংশ ক/খ পাওয়া সম্ভবই না, যা দিয়ে অতিভুজটিকে প্রকাশ করা যায়। ইউক্লিডের জ্যামিতি বইয়ের দশম পর্বে এই প্রমাণটিই আছে [ছ]।
এই যুক্তিটি প্রমাণ করে – যে একক নিয়েই আমরা কাজ করি না কেন, কিছু দৈর্ঘ্য আছে, যার সঙ্গে এককটির কোনো যথাযথ আঙ্কিক সম্পর্ক নেই, অর্থাৎ, এমন কোনো দুটি পূর্ণসংখ্যা ক, খ পাওয়া সম্ভব না, যাতে ক পরিমাণ সেই দৈর্ঘ্যটি খ পরিমাণ একক-এর সঙ্গে সমান। গ্রিক গণিতবিদরা এর ফলে নিঃসন্দেহ হলেন, যে, জ্যামিতিকে পাটীগণিত-এর থেকে আলাদাভাবে উপস্থাপন করতে হবে। প্লেটো-র সময়ে জ্যামিতির এই স্বাধীনতা অর্জন যে পুরোদমে চলছিল, তার প্রমাণ তাঁর ‘ডায়ালগ’-এর বেশ কিছু অনুচ্ছেদ থেকে পাওয়া যায়, আর এই চেষ্টা পূর্ণতা পায় ইউক্লিডের সময়ে। ইউক্লিড তাঁর বইয়ের দ্বিতীয় পর্বে এমন অনেক গাণিতিক সম্পর্কের জ্যামিতিক প্রমাণ দিয়েছেন, যা আমরা সহজেই বীজগণিতের সাহায্যে প্রমাণ করতে পারি, যেমন, 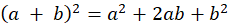 । অসমগুণনীয়কের সমস্যার কারণেই তিনি এই পাঠ্যাংশের প্রয়োজন অনুভব করেছিলেন বলে মনে হয়। তাঁর বইয়ের পাঁচ আর ছয় পর্বের অনুপাত-অংশটির জন্যেও একই কথা প্রযোজ্য। গোটা প্রণালীটি অসামান্যরকম যুক্তিগ্রাহ্য, আর যেন ঊনবিংশ শতকের কঠিন নিয়মানুবদ্ধ অঙ্ক কষার পূর্বসূরী। যতক্ষণ না অসমগুণনীয়কের কোনো উপযুক্ত পাটীগাণিতিক ব্যাখ্যা পাওয়া যায়—জ্যামিতিতে যতটুকু করা সম্ভব, ইউক্লিডের পদ্ধতি ছিল তার সর্বশ্রেষ্ঠ নিদর্শন। দেকার্তে যখন স্থানাঙ্ক জ্যামিতির উপস্থাপন করে আবার পাটীগণিতকে শীর্ষে তুলে আনলেন, অসমগুণনীয়কের সমস্যা সমাধানের এক সম্ভাবনা তিনি ধরে নিয়েছিলেন, যদিও তাঁর সময়ে এ সমস্যার কোনো সমাধান পাওয়া যায়নি।
। অসমগুণনীয়কের সমস্যার কারণেই তিনি এই পাঠ্যাংশের প্রয়োজন অনুভব করেছিলেন বলে মনে হয়। তাঁর বইয়ের পাঁচ আর ছয় পর্বের অনুপাত-অংশটির জন্যেও একই কথা প্রযোজ্য। গোটা প্রণালীটি অসামান্যরকম যুক্তিগ্রাহ্য, আর যেন ঊনবিংশ শতকের কঠিন নিয়মানুবদ্ধ অঙ্ক কষার পূর্বসূরী। যতক্ষণ না অসমগুণনীয়কের কোনো উপযুক্ত পাটীগাণিতিক ব্যাখ্যা পাওয়া যায়—জ্যামিতিতে যতটুকু করা সম্ভব, ইউক্লিডের পদ্ধতি ছিল তার সর্বশ্রেষ্ঠ নিদর্শন। দেকার্তে যখন স্থানাঙ্ক জ্যামিতির উপস্থাপন করে আবার পাটীগণিতকে শীর্ষে তুলে আনলেন, অসমগুণনীয়কের সমস্যা সমাধানের এক সম্ভাবনা তিনি ধরে নিয়েছিলেন, যদিও তাঁর সময়ে এ সমস্যার কোনো সমাধান পাওয়া যায়নি।
দর্শন ও বৈজ্ঞানিক পদ্ধতির ওপর জ্যামিতির গভীর প্রভাব। গ্রিকরা যেভাবে জ্যামিতির প্রস্তাবনা করেছেন, তা শুরু হয় কিছু স্বতঃসিদ্ধ (axiom) দিয়ে, যেগুলি নিজেই নিজেই সিদ্ধ/প্রমাণিত (বা অন্তত এমনটা তাদের সম্পর্কে ভাবা হয়), আর তারপর তার থেকে অবরোহী যুক্তির মাধ্যমে এমন সব উপপাদ্যের প্রমাণ করা হয়, যারা মোটেও আপাতদৃষ্টিতে সহজে প্রমাণিত নয়। এই স্বতঃসিদ্ধ ও উপপাদ্যগুলি পার্থিব স্থান (space)-এর ক্ষেত্রে প্রযোজ্য, তাই অভিজ্ঞতা দিয়ে যাচাইযোগ্য। অতএব, স্বতঃসিদ্ধগুলিকে চিহ্নিত করে, অবরোহী যুক্তির প্রয়োগ করে, বাস্তব জগতের সম্পর্কে নতুন আবিষ্কার করা সম্ভব। এই অভিমতটি প্লেটো থেকে কান্ট ও অন্তর্বর্তী সব দার্শনিককেই প্রভাবিত করেছিল। যখন ‘স্বাধীনতার ঘোষণাপত্র’ (আমেরিকার)-তে লেখা হয়, “এই সত্যগুলিকে আমরা স্বতঃসিদ্ধ বলে মনে করি” (we hold these truths to be self-evident), তখন তার আদর্শ আসলে ইউক্লিড। অষ্টাদশ শতকের প্রাকৃতিক অধিকারের (natural rights) নিয়মাবলী আসলে রাজনীতিতে ইউক্লিডীয় স্বতঃসিদ্ধের সন্ধান [জ]। নিউটনের ‘প্রিন্সিপিয়া’ যদিও স্পষ্টতই পরীক্ষাভিত্তিক উপাদান দিয়ে ভরা, তবু তাতে ইউক্লিডের আধিপত্য প্রশ্নাতীত। ধর্মতত্ত্বও, তার নির্দিষ্ট পণ্ডিতি চেহারায়, একই উৎস থেকে নিজের কেতা ধার করে। ব্যক্তিগত ধর্মাচরণ ‘দিব্য-পরমানন্দের’ থেকে আহরিত হলেও, ধর্মতত্ত্ব আসে অঙ্ক থেকেই; আর এর দুই-ই পাওয়া যায় পিথাগোরাসে।
আমার ধারণা, গণিত যেমন এক নির্দিষ্ট চিরসত্যে বিশ্বাস আনে, তেমনই, এক অতি-বোধগম্য, পার্থিব জগতের অস্তিত্বে বিশ্বাসের উৎসও অঙ্কই। আদর্শ বৃত্ত নিয়ে জ্যামিতির কারবার, কিন্তু কোনো পার্থিব বস্তুই নিখুঁত বৃত্তাকার হয় না; যতই সন্তর্পণে কম্পাস ব্যবহার করি না কেন—কিছু খুঁত, কিছু অসামঞ্জস্য এসেই পড়ে। এর থেকে ধারণা হওয়া স্বাভাবিক – সব নিখুঁত যুক্তিই আসলে—ইন্দ্রিয়গ্রাহ্য নয়—আদর্শ বস্তুর ক্ষেত্রে প্রযোজ্য; একধাপ আরও এগিয়ে এমন ভাবাও স্বাভাবিক — চিন্তার/মননের স্থান ইন্দ্রিয়ের উপরে, আর কল্পিত আদর্শ বস্তু আসলে ইন্দ্রিয়গ্রাহ্য বস্তুর চেয়ে বেশি বাস্তব। যেসব অতীন্দ্রিয় শাস্ত্র সময়ের ঊর্ধ্বে চিরায়তের কথা বলে, বিশুদ্ধ গণিত তাদেরও জোর যোগায়, কারণ, গাণিতিক বস্তুগুলি—যেমন সংখ্যা—সময়ের বাইরে, তাদের অস্তিত্ব চিরকালীন। এই শাশ্বত বস্তুগুলিকে ‘ঈশ্বরের ভাবনা’ হিসেবে ভাবা সম্ভব। এইকারণেই প্লেটোর নির্দেশ – ঈশ্বর একজন জ্যামিতিবেত্তা, আর স্যার জেমস জিন্স-এর বিশ্বাস – তিনি পাটীগণিত-এর নেশাড়ু। পিথাগোরাসের সময় থেকে, এবং উল্লেখযোগ্যভাবে প্লেটোর পরবর্তীকালে যুক্তিবাদী ধর্মে (প্রলয়ের ডঙ্কাবাদক ধর্ম নয়) পূর্ণরূপে গণিত ও গাণিতিক পদ্ধতির আধিপত্য। পিথাগোরাসে শুরু হওয়া গণিত ও ধর্মতত্ত্বের এই মিশেল—গ্রিস থেকে শুরু করে মধ্যযুগ হয়ে আধুনিক যুগে কান্ট অবধি—ধর্মীয় দর্শনের চরিত্র নিরূপণ করেছে। পিথাগোরাসের আগে অর্ফিজ়ম ছিল এশীয় রহস্যাবৃত ধর্মগুলির (mystery religions) মতো, কিন্তু প্লেটো, সন্ত অগাস্টিন, থমাস অ্যাকুইনাস, দেকার্তে, স্পিনোজ়া আর লাইবনিৎজ়-এর মধ্যে – ধর্মের সঙ্গে যুক্তির, নৈতিক আকাঙ্খার সঙ্গে চিরায়তের প্রতি যৌক্তিক সমীহ-র এক ঘনিষ্ঠ সংমিশ্রণ ঘটেছিল—যার শুরু পিথাগোরাসে; এশীয় অতীন্দ্রিয়বাদের থেকে এটিই ইউরোপের বৌদ্ধিক ধর্মতত্ত্বকে আলাদা করেছিল। পিথাগোরাস ঠিক কোন কোন ক্ষেত্রে ভুল ছিলেন, তা কেবল অতি সম্প্রতিই নিশ্চিত করে বলা সম্ভব হয়েছে। চিন্তার জগতে তাঁর থেকে বেশি প্রভাবশালী আর কোনো ব্যক্তিত্ত্বের কথা অন্তত আমার জানা নেই। আমার এ কথা বলার কারণ: আপাতদৃষ্টিতে যা প্লেটোনিজ়ম বলে প্রতিভাত হয়, তার বিশ্লেষণ করলে পিথাগোরিয়ানিজ়ম-ই পাওয়া যায়। ইন্দ্রিয়ের অতীত এক চিরায়ত জগত, যা কেবল বুদ্ধিবৃত্তির কাছেই আত্মপ্রকাশ করে – এ ধারণা তাঁর থেকেই ধার করা। তিনি না থাকলে খ্রিস্টানরা যীশু-কে ‘বাণী’ বলে ভাবতে পারতো না (অনুবাদক: ‘the Word’; আগের পর্বের শেষ টিপ্পনীর ‘আদি-তে ছিল শব্দ…’ মনে আছে তো?); তাঁর অনুপস্থিতিতে অমরত্ব বা ঈশ্বরের যৌক্তিক ‘প্রমাণ’ সংগ্রহে ব্যস্ত হতেন না ধর্মতাত্ত্বিকেরা। তবে, তাঁর ক্ষেত্রে এ সব-ই অব্যক্ত। কী করে সেসব সুব্যক্ত, স্পষ্ট হল – তা আমরা যত এগোবো, আরো পরিষ্কার হবে।
চলবে... (এর পরের পর্ব: হেরাক্লিতোস)
— বার্ট্রান্ড রাসেল
A History of Western Philosophy বইটির তৃতীয় পরিচ্ছেদের প্যালারাম-কৃত অনুবাদ
টীকা-টিপ্পনীর ব্র্যাকেটের মধ্যে অক্ষর থাকলে তা রাসেলের আসল ফুটনোট, সংখ্যা থাকলে তা অনুবাদকের পাকামো। ফুটনোট কণ্টকিত লেখাটির জন্যে ক্ষমাপ্রার্থী, তবে ছবি-ছাবা দিয়ে সেই দোষ স্খালনের একটা চেষ্টা করা হয়েছে।
[ক] সিসিলির গ্রিক নগরীগুলির ওপর কার্থেজের আক্রমণের ভয় থাকলেও, ইতালিতে তেমন কোনো আশু সম্ভাবনা ছিল না।
[খ] আরিস্তোতল তাঁর সম্পর্কে বলেছেন যে তিনি 'প্রথমে অঙ্ক আর পাটীগণিত-এ কাজ করতেন, তারপর একসময় ফেরেকিদিস-এর প্রদর্শিত পথে অতিপ্রাকৃত চর্চাকারী মুরুব্বিতে পরিণত হন'।
[গ] “... ভাঁড়: বুনোমুরগি নিয়ে পিথাগোরাসের ধ্যানধারণা যেন ঠিক কী?
ম্যালভোলিও: তাঁর ধারণা – এমনও হতে পারে, যে, আমাদের পিতামহীর আত্মা তার ভেতর বাস করছে।
ভাঁড়: আর তেনার এই ধারণা সম্পর্কে আপনার কী মত?
ম্যালভোলিও: আত্মাকে আমি যথেষ্ট সম্মান করি, অতএব তাঁর এই মতটি মোটেও সমর্থন করি না।
ভাঁড়: ভালো থাকবেন, আমি এলাম। থাকুন বসে অন্ধকারে। আগে পিথাগোরাসে বিশ্বাস আনুন, আর পাছে ঠাকুমার আত্মাকে খাঁচাছাড়া করতে হয়—সেই ভয়ে তিতির মারতেও ভয় পেতে শুরু করুন, তবে মানবো, যে আপনার মতিস্থির আছে। বিদায়।”
“...Clown: What is the opinion of Pythagoras concerning wild fowl?
MALVOLIO: That the soul of our grandam might haply inhabit a bird.
Clown: What thinkest thou of his opinion?
MALVOLIO: I think nobly of the soul, and no way approve his opinion.
Clown: Fare thee well. Remain thou still in darkness: thou shalt hold the opinion of Pythagoras ere I will allow of thy wits, and fear to kill a woodcock, lest thou dispossess the soul of thy grandam. Fare thee well....”
— Twelfth Night, Shakespeare
[ঘ] Burnet-এর Early Greek Philosophy থেকে উদ্ধৃত
[ঙ] কর্নফোর্ডের বইয়ের ২০১ নং পৃষ্ঠা দেখুন।
[চ] বার্নেটের বইয়ের ১০৮ নং পৃষ্ঠা দেখুন।
[ছ] কিন্তু তা ইউক্লিডের প্রমাণ করা নয়। Heath-এর Greek Mathematics বইটি দেখুন। সম্ভবত এই প্রমাণটি প্লেটোরও জানা ছিল।
[জ] জেফারসন লিখেছিলেন ‘পবিত্র ও অনস্বীকার্য’ (sacred and undeniable), ফ্র্যাঙ্কলিন তাকে বদলে ‘স্বতঃসিদ্ধ’ (self-evident) করেন।
[১] হার্মান ভলিং-এর মতে এই নৌবহরটি আমাসিস-এর খরচে নির্মিত, পোলিক্রাতিসের সৈন্য দিয়ে সাজানো এবং পারস্যের উদ্দেশে পাঠানো হয়েছিল, অন্যদিকে হান্স ভ্যান ভিস-এর ধারণা ঠিক উলটো – নৌবহরটি পারস্যের উপহার, পোলিক্রাতিস-এর সৈন্য দিয়ে ভরা আর আমাসিস-এর বিরুদ্ধে পাঠানো। রাসেল এখানে দ্বিতীয় মতটি সমর্থন করছেন আর রাজনৈতিক প্রতিপক্ষ বলতে সামিওস-বাসী বিরুদ্ধপক্ষের কথাই বলছেন খুব সম্ভবত।
চলবে... (এর পরের পর্ব: হেরাক্লিতোস)
পুনঃপ্রকাশ সম্পর্কিত নীতিঃ এই লেখাটি ছাপা, ডিজিটাল, দৃশ্য, শ্রাব্য, বা অন্য যেকোনো মাধ্যমে আংশিক বা সম্পূর্ণ ভাবে প্রতিলিপিকরণ বা অন্যত্র প্রকাশের জন্য গুরুচণ্ডা৯র অনুমতি বাধ্যতামূলক। লেখক চাইলে অন্যত্র প্রকাশ করতে পারেন, সেক্ষেত্রে গুরুচণ্ডা৯র উল্লেখ প্রত্যাশিত।

প্যালারাম লেখকের গ্রাহক হোন






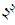 , আবার বর্গক্ষেত্রও বটে) ‘কিউব’ (ঘন, যেমন
, আবার বর্গক্ষেত্রও বটে) ‘কিউব’ (ঘন, যেমন 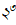 , আবার ঘনক-ও) নিয়ে কথা বলি, যে শব্দগুলির জন্যে আমরা তাঁর কাছে ঋণী। তিনি আয়ত-বৃত্তাকার/ডিম্বাকৃতি (oblong), ত্রিভুজাকৃতি, বা পিরামিডাকৃতি সংখ্যার কথাও বলেছিলেন। কোনো একটি আকৃতি তৈরি করতে যতগুলি নুড়ি-পাথর (আমরা কড়ি-ও ভাবতে পারি) লাগে, আকৃতিটি সেই সংখ্যার সঙ্গে যুক্ত। সম্ভবত তিনি জগতের এক পারমাণবিক ছবিতে বিশ্বাস করতেন, যেখানে পরমাণুগুলি নানা আকৃতিতে জুড়ে জুড়ে পদার্থের অণুগুলির গঠন করে। তাঁর আশা ছিল, এইভাবেই পাটীগণিত – পদার্থবিদ্যা তথা নন্দনতত্ত্বেরও অপরিহার্য পাঠ হয়ে উঠবে।
, আবার ঘনক-ও) নিয়ে কথা বলি, যে শব্দগুলির জন্যে আমরা তাঁর কাছে ঋণী। তিনি আয়ত-বৃত্তাকার/ডিম্বাকৃতি (oblong), ত্রিভুজাকৃতি, বা পিরামিডাকৃতি সংখ্যার কথাও বলেছিলেন। কোনো একটি আকৃতি তৈরি করতে যতগুলি নুড়ি-পাথর (আমরা কড়ি-ও ভাবতে পারি) লাগে, আকৃতিটি সেই সংখ্যার সঙ্গে যুক্ত। সম্ভবত তিনি জগতের এক পারমাণবিক ছবিতে বিশ্বাস করতেন, যেখানে পরমাণুগুলি নানা আকৃতিতে জুড়ে জুড়ে পদার্থের অণুগুলির গঠন করে। তাঁর আশা ছিল, এইভাবেই পাটীগণিত – পদার্থবিদ্যা তথা নন্দনতত্ত্বেরও অপরিহার্য পাঠ হয়ে উঠবে।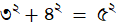 , আর এই আন্দাজ থেকেই সাধারণ নিয়মটির এক প্রমাণ আবিষ্কার করেন।
, আর এই আন্দাজ থেকেই সাধারণ নিয়মটির এক প্রমাণ আবিষ্কার করেন।
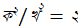 । ক এবং খ-এর গ.সা.গু দিয়ে দুই রাশিকেই ভাগ করলে যা পড়ে থাকে, তার একটি তবে অবশ্যই বিজোড় (দুটি-ই জোড় হলে তার ২ তবে গ.সা.গু-র মধ্যে চলে যায়)। যেহেতু
। ক এবং খ-এর গ.সা.গু দিয়ে দুই রাশিকেই ভাগ করলে যা পড়ে থাকে, তার একটি তবে অবশ্যই বিজোড় (দুটি-ই জোড় হলে তার ২ তবে গ.সা.গু-র মধ্যে চলে যায়)। যেহেতু 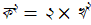 , অর্থাৎ ক জোড় সংখ্যা, খ নিশ্চয়ই তবে বিজোড়। এবার
, অর্থাৎ ক জোড় সংখ্যা, খ নিশ্চয়ই তবে বিজোড়। এবার 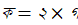 ধরলে,
ধরলে, 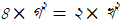 , অতএব
, অতএব 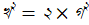 , মানে খ জোড়সংখ্যা – মূল প্রতিপাদ্যটি ভুল প্রমাণিত হল। তাহলে এমন কোনো ভগ্নাংশ ক/খ পাওয়া সম্ভবই না, যা দিয়ে অতিভুজটিকে প্রকাশ করা যায়। ইউক্লিডের জ্যামিতি বইয়ের দশম পর্বে এই প্রমাণটিই আছে [ছ]।
, মানে খ জোড়সংখ্যা – মূল প্রতিপাদ্যটি ভুল প্রমাণিত হল। তাহলে এমন কোনো ভগ্নাংশ ক/খ পাওয়া সম্ভবই না, যা দিয়ে অতিভুজটিকে প্রকাশ করা যায়। ইউক্লিডের জ্যামিতি বইয়ের দশম পর্বে এই প্রমাণটিই আছে [ছ]।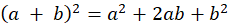 । অসমগুণনীয়কের সমস্যার কারণেই তিনি এই পাঠ্যাংশের প্রয়োজন অনুভব করেছিলেন বলে মনে হয়। তাঁর বইয়ের পাঁচ আর ছয় পর্বের অনুপাত-অংশটির জন্যেও একই কথা প্রযোজ্য। গোটা প্রণালীটি অসামান্যরকম যুক্তিগ্রাহ্য, আর যেন ঊনবিংশ শতকের কঠিন নিয়মানুবদ্ধ অঙ্ক কষার পূর্বসূরী। যতক্ষণ না অসমগুণনীয়কের কোনো উপযুক্ত পাটীগাণিতিক ব্যাখ্যা পাওয়া যায়—জ্যামিতিতে যতটুকু করা সম্ভব, ইউক্লিডের পদ্ধতি ছিল তার সর্বশ্রেষ্ঠ নিদর্শন। দেকার্তে যখন স্থানাঙ্ক জ্যামিতির উপস্থাপন করে আবার পাটীগণিতকে শীর্ষে তুলে আনলেন, অসমগুণনীয়কের সমস্যা সমাধানের এক সম্ভাবনা তিনি ধরে নিয়েছিলেন, যদিও তাঁর সময়ে এ সমস্যার কোনো সমাধান পাওয়া যায়নি।
। অসমগুণনীয়কের সমস্যার কারণেই তিনি এই পাঠ্যাংশের প্রয়োজন অনুভব করেছিলেন বলে মনে হয়। তাঁর বইয়ের পাঁচ আর ছয় পর্বের অনুপাত-অংশটির জন্যেও একই কথা প্রযোজ্য। গোটা প্রণালীটি অসামান্যরকম যুক্তিগ্রাহ্য, আর যেন ঊনবিংশ শতকের কঠিন নিয়মানুবদ্ধ অঙ্ক কষার পূর্বসূরী। যতক্ষণ না অসমগুণনীয়কের কোনো উপযুক্ত পাটীগাণিতিক ব্যাখ্যা পাওয়া যায়—জ্যামিতিতে যতটুকু করা সম্ভব, ইউক্লিডের পদ্ধতি ছিল তার সর্বশ্রেষ্ঠ নিদর্শন। দেকার্তে যখন স্থানাঙ্ক জ্যামিতির উপস্থাপন করে আবার পাটীগণিতকে শীর্ষে তুলে আনলেন, অসমগুণনীয়কের সমস্যা সমাধানের এক সম্ভাবনা তিনি ধরে নিয়েছিলেন, যদিও তাঁর সময়ে এ সমস্যার কোনো সমাধান পাওয়া যায়নি। dc | 2402:e280:2141:1e8:a4a2:42fa:3775:***:*** | ২৬ নভেম্বর ২০২৪ ১৯:১০539666
dc | 2402:e280:2141:1e8:a4a2:42fa:3775:***:*** | ২৬ নভেম্বর ২০২৪ ১৯:১০539666 &/ | 151.14.***.*** | ২৭ নভেম্বর ২০২৪ ০১:৩২539684
&/ | 151.14.***.*** | ২৭ নভেম্বর ২০২৪ ০১:৩২539684বিপ্লব রহমান | ২৭ নভেম্বর ২০২৪ ০৮:০৯539691
 কালনিমে | 103.244.***.*** | ২৭ নভেম্বর ২০২৪ ২০:৫৫539714
কালনিমে | 103.244.***.*** | ২৭ নভেম্বর ২০২৪ ২০:৫৫539714অমিতাভ চক্রবর্ত্তী | ২৮ নভেম্বর ২০২৪ ০৯:৫৩539721
রমিত চট্টোপাধ্যায় | ২৮ নভেম্বর ২০২৪ ১০:৫৩539722














