প্রথম পর্ব এখানে -     https://www.guruchandali.com/comment.php?topic=17281
দ্বিতীয় পর্ব এখানে-   https://www.guruchandali.com/comment.php?topic=17291

সাল ১৯২৪। ফরাসী বিজ্ঞানী ডি ব্রোয়ি চিন্তা করেন, আলো, যাকে তরঙ্গ ভাবা হত, যদি কণার মত আচরণ করতে পারে, তবে যাকে আমরা কণা হিসাসবে ভাবি, তারও তরঙ্গ ধর্ম থাকা অস্বাভাবিক নয়। তিনি তাঁর এই চিন্তা থেকে ইলেক্ট্রন কণার তরঙ্গ ধর্মের ধারণা দেন। λ  তরঙ্গদৈর্ঘের কোন কণার ভরবেগ যদি p হয়, তবে,

     p  =                  h= প্ল্যাঙ্ক ধ্রুবক

এই তত্ত্বের ভিত্তিতে কোয়াণ্টাম মেকানিক্স এর ভিত্তি গড়ে ওঠে।

ইলেক্ট্রন বিচ্ছুরণ পরীক্ষা (Electron Diffraction Experiment)

ডি ব্রোয়ির সূত্র প্রমাণিত হয় তিন বছর পর, দুটি স্বাধীন ভিন্ন ইলেক্ট্রন বিচ্ছুরণ পরীক্ষার মাধ্যমে।

প্রথম পরীক্ষায় আবেরডিন বিশ্ববিদ্যালয়ে জর্জ থমসন ইলেক্ট্রন গানের সাহায্যে পাতলা ধাতব ফিল্মে ইলেক্ট্রন বিচ্ছুরণ ঘটিয়ে ডি ব্রোয়ি বর্ণিত তবঙ্গের ব্যতিচার ধর্ম ইলেক্ট্রন তরঙ্গের মধ্যে দেখতে পান।
দ্বিতীয় পরীক্ষায়, বেল ল্যাবে, ক্লিন্টন ডেভিসন ও ল্যাস্টার গ্রামার ইলেক্ট্রনগুলি একে অপরের সাথে সংঘর্ষ যাতে না ঘটে, সে কারণে বিচ্ছিন্ন ভাবে একটি একটি করে ইলেক্ট্রন পাঠিয়েও ব্যতিচার ধর্ম লক্ষ্য করলেন। তাঁরা প্রকৃত কারণ অনুসন্ধানের জন্য প্লেটের উপরের ছিদ্রে ইলেক্ট্রন ডিটেক্টর স্থাপন করলেন। এরপর ইলেক্ট্রন বিম পাঠিয়ে দেখলেন ফিল্মের গায়ে দুটি নিরবিচ্ছিন্ন রেখা দেখা গেছে, যা আগের ফলাফল অপেক্ষা আলাদা।

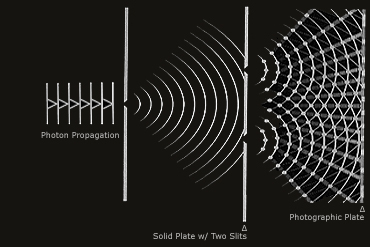
          ইলেক্ট্রন বিচ্ছুরণ পরীক্ষা 

তাঁরা দুটি ক্ষেত্রে ভিন্ন ভিন্ন ফল যা পেলেন, তার ব্যাখ্যা খুঁজে পেলেন না।

সাল ১৯২৫। হাইজেনবার্গ বোর মডেলের হাইড্রোজেন গ্যাসের আলোক বর্ণালীর তীব্রতার ব্যাখ্যা দিতে গিয়ে কোয়াণ্টাম মেকানিক্স তত্ত্বের জন্ম দিলেন। তিনি তাঁর অনিশ্চয়তা নীতির সূত্রে ( Heisenberg’s uncertainty principle) দেখালেন,

  ∆ x ∆p ≥  h      যেখানে, ∆ =  অতি ক্ষুদ্র পরিবর্তন।

                 x =  কণার অবস্থান।

                 p =  কণার ভরবেগ।    

                 h =  অর্ধ প্ল্যাঙ্ক ধ্রুবক

হাইজেন বার্গ ব্যাখ্যা দিলেন, কণার অবস্থান ও ভরবেগ পরিমাপের ক্ষেত্রে অনিশ্চয়তার ঘটনা পরিলক্ষিত হবে। যদি কণার অবস্থান নির্ণয় করা হয়, তবে একইসাথে পদার্থের ভরবেগ নির্ণয় করা সম্ভব হবে না। আবার কণার ভরবেগ নির্ণয় করতে গেলে পদার্থের সঠিক অবস্থান নির্ণয় করা সম্ভব নয়।

এই একই সময়ে ডি ব্রোয়ির (De Broglie) নীতির উপর ভিত্তি করে এরুইন স্ক্রোডিঙ্গার কোয়াণ্টাম মেকানিকাল তরঙ্গের ব্যাখ্যা দিতে গাণিতিক সূত্র রচনা করেন যা ‘স্ক্রোডিঙ্গার সূত্র’ (Schrodinger Equation) নামে পরিচিত। তাঁর এই সূত্র কোয়াণ্টাম মেকানিক্সের কোন কণার স্বীকৃত স্থিতিশীল অবস্থানের গাণিতিক ব্যাখ্যা দেয় এবং কোয়াণ্টাম বিদ্যায় সময়ের সাথে বাহ্যিক পরিবর্তনের ধারণা দেয়।

সাল ১৯২৪। উলফগান পাউলি ধারণা দিয়েছিলেন, “একই পরমাণুতে দুটি ইলেক্ট্রনের চারটি কোয়ান্টাম সংখ্যার মাণ এক হতে পারে না।” তাঁর এই ধারণাকে পাউলি র বর্জন নীতি (Pauli’s Exclusion Principle) হিসাবে ধরা হয়।

কিন্ত দেখা গেছে, দুটি ইলেক্ট্রনের কোয়াণ্টাম অবস্থা পারস্পরিক নির্ভরশীল হতে পারে। একে ‘কোয়াণ্টাম জট’ বা ‘Quantum Entanglement’ বলা হয়। একটু বিস্তৃতভাবে ব্যাখ্যা করলে বলা যেতে পারে, যখন দুটো কণা বা কণাগুচ্ছ একই সাথে উৎপণ্ণ হয়, বা পারষ্পরিক আন্তক্রিয়াশীল, সেক্ষেত্রে একটি কণার কোয়াণ্টাম অবস্থা অন্য কণার সাপেক্ষে নিরপেক্ষ ব্যাখ্যা দেওয়া সম্ভব নয়। এক্ষেত্রে কণাগুলির কোয়াণ্টাম অবস্থার একত্রে ব্যাখ্যা দেওয়া সম্ভব। এই অবস্থাকে ‘কোয়াণ্টাম জট’ বা ‘কোয়াণ্টাম এণ্টাঙ্গেলমেণ্ট’ বলা হয়।
দেখা গেছে কোয়াণ্টাম জটযুক্ত কণাসমষ্ঠীর অবস্থান, ভরবেগ, ঘুর্ণণ, পোলারাইজেশন ইত্যাদি বাহ্যিক পরিমাপ সম্পূর্ণ পারস্পরিকভাবে নির্ভরশীল। ধরা যাক, এক জোড়া কোয়াণ্টাম জটযুক্ত কণার উতপত্তি হল যাদের সম্পূর্ণ ঘূর্ণণ কোন এক নির্দিষ্ট অক্ষ রেখার সাপেক্ষে শূণ্য। এক্ষেত্রে একটি কণার ঘুর্ণণ নির্দিষ্ট অক্ষের সাপেক্ষে যদি ঘড়ির কাঁটার দিকে হয়, তবে অন্য কণার ঘুর্ণণ নির্দিষ্ট অক্ষের সাপেক্ষে যদি ঘড়ির কাঁটার বিপরীতমুখী হবে। এবং এদের মাণ পরষ্পর সমান কিন্ত বিপরীত দশায় অবস্থানের কারণে যোগফল শূণ্য।

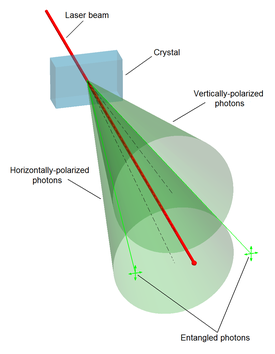
            কোয়াণ্টাম জট 

উপরের বিস্তৃত আলোচনা থেকে আমরা কোয়াণ্টামতত্ত্ব কি এবং কোয়াণ্টাম কণার দ্বৈতস্বত্তা সম্পর্কে একটা ধারণা পেলাম। এবার আমরা যাব পরবর্তী আলোচনায়। এখান থেকে আমরা বোঝার চেষ্টা করব কোয়াণ্টাম আধিপত্য (Quantum Supremacy) কি?

আমরা কোয়াণ্টাম তত্ত্ব আলোচনার আগে প্রচলিত দ্বন্দ্ব নিয়ে আলচনা শুরু করেছিলাম, এক্ষেত্রে দ্বিতীয় পর্বের আলোচনা শুরু করব একটু অন্যভাবে। আমরা আগে বোঝার চেষ্টা করব একটা কোয়ান্টাম কম্পিউটার পেলে আমাদের ব্যবহারিক জীবনে লাভ কোথায়?

ধরা যাক, আমার কাছে আদ্দিকালের কোলকাতা ফোন ডাইরেক্টরি আছে। আমি একজনের ফোন নম্বর খুঁজতে চাই যার নম্বর হল ০৪৩-২৩৪। এটা করতে গেলে আমাকে ফোন বইতে যতগুলো নম্বর আছে প্রত্যেকটাই একবার করে মেলাতে হবে। যদি ১০ লক্ষ ফোন নম্বর থাকে তবে ১০ লক্ষবার। কিন্ত ১৯৯৬ সালে বেল ল্যাবে লব গ্রোভার এই একই কাজ কোয়াণ্টাম কম্পিউটারের সাহায্যে করে ১০০০ বারে করেছিলেন। (অবশ্য ফোন বইটা আমেরিকার ছিল যদিও)।
আরেকটা উদাহরণ দেওয়া যাক, যদি আমাদের বড় আকারের নম্বরের তথ্য থাকে, (ধরা যাক, দশ লক্ষ) তার মধ্যে থেকে দুটি সমান সংখ্যার নম্বর যদি খুঁজে পেতে হয় সেক্ষেত্রে সাধারণ কম্পিউটার ১০ লক্ষবার মিলিয়ে তবে সম্ভাব্য নম্বর দুটি খুঁজে দেবে। কিন্তু কোয়ান্টাম কম্পিউটারের কাছে এই খোঁজার সময়টা খুব কম লাগবে।
অর্থাৎ একটা সাধারণ কম্পিউটার এক সাথে একটি সমস্যার সমাধান করতে সক্ষম, অন্যদিকে একটা কোয়াণ্টাম কম্পিউটার একসাথে অনেক সমস্যার সমাধান করে ফেলতে পারে। কোয়াণ্টাম কম্পিউটার আবিষ্কৃত হলে সুরক্ষাক্ষেত্রে, স্বাস্থ্য পরিষেবা ইত্যাদিতে বিশ্বজগতে যে আমূল পরিবর্তন ঘটবে, তা বলার অপেক্ষা রাখে না।
বাস্তবে আমাদের জীবনে হ্যাকারদের প্রাদুর্ভাব হামেশাই দেখতে পাই। ব্যাঙ্ক থেকে চোখের নিমেষে টাকা গায়েব নিত্যনৈমিত্তিক ব্যাপার। কিন্ত কোয়াণ্টাম কম্পিউটার আবিষ্কার হলে ইন্টারনেট জগতে সুরক্ষা প্রতিষ্ঠিত হবে এবং ই চুরি কমে যাবে তা বলার অপেক্ষা রাখে না।
অন্যদিকে, ওষুধ তৈরীর ক্ষেত্রে পরমাণুর কোয়াণ্টাম প্রকৃতি সম্পর্কে সুপার কম্পিউটার দিয়েও সঠিকভাবে জানা সম্ভব না হওয়ার ফলে বড় বড় অসুখের ক্ষেত্রে সঠিক ওষুধ তৈরী একটা সমস্যা হয়ে দাঁড়ায়। কিন্ত কোয়াণ্টাম কম্পিউটার আবিষ্কার হলে আমরা আলঝাইমার এর মত কঠিন অসুখের সাথেও লড়তে পারব।
অর্থনৈতিক ভাবে শক্তিশালী দেশগুলি কোয়াণ্টাম কম্পিউটারের ব্যবহারিক দিক নিয়ে যথেষ্ট ওয়াকিবহাল। আমেরিকার ডিফেন্স অরগানাইজেশন ‘ডি ওয়েভ’ নামে বড় কোয়াণ্টাম কম্পিউটার ব্যবহার করে। চীন কোয়াণ্টাম কম্পিউটার গড়তে তিন বছরে ১০ বিলিয়ন ডলার খরচ করে চলেছে যা আমেরিকার কোয়াণ্টাম কমপিউটার তৈরী খরচের থেকে ১৩% বেশি।

এবার একটা সাধারণ সমস্যা দিয়ে দ্বিতীয় পর্বের আলোচনা এগিয়ে নিয়ে যাব।

সিদ্ধান্ত নির্ণয়ক সমস্যা(Entscheidungs Problem)

সতেরশ শতকে গোট্টফ্রিড লেইবনিজ ( Gottfried Leibniz) মেকানিক্যাল গণণাযন্ত্র (mechanical calculator)  আবিষ্কারের পর এমন একটা মেশিনের কল্পনা করতে লাগলেন যা শুধুমাত্র চিহ্ন উৎপন্ন করে কোন গাণিতিক বিবৃতির সততার মাণ(truth value) নির্ণয় করবে। তিনি অনুভব করলেন এক্ষেত্রে প্রাথমিক রূপে একটা সহজ ভাষা গঠন করা প্রয়োজন।

সাল ১৯২৮। ডেভিড হিলবার্ট (David Hilbert) এবং উইলহেম একেরম্যান (Wilhem Ackermann) লেইবনিজের ধারণাকে ভিত্তি করে সিদ্ধান্ত নির্ণায়ক সমস্যা (Entscheidungs Problem)-র জন্ম দেন। এই সমস্যা অনুযায়ী তাঁরা প্রশ্ন রাখেন এমন কোন Algorithm(পদ্ধতি)আছে যা যুক্তিপূর্ণ বিবৃতি যুক্ত ভাষা গ্রহণ করবে এবং বিবৃতির সততার মাণ ফলাফল হিসাবে ‘হ্যাঁ’ বা ‘না’ তে দেবে? উত্তর যতক্ষণ সঠিক থাকবে Algorithm তার স্বপক্ষে কোন প্রমাণ দেবে না বা জানাবে না কি করে উত্তর পাওয়া গেল।

টুরিং মেশিন (Turing Machine)

সাল ১৯৩৬। অ্যালান টুরিং  (Alan Turing) একটি স্বয়ংক্রিয় যন্ত্র আবিষ্কার করলেন যার নাম দিলেন ‘টুরিং মেশিন’। তিনি এই মেশিন মডেলের স্বাপেক্ষে নঞর্থকভাবে দুটি প্রশ্নের উত্তর দিতে সক্ষম হলেন,

১)বাস্তবে কোন মেশিন অবস্থান করে কিনা যে তার ফিতের উপর কোন কাল্পনিক মেশিন গোলাকার (অর্থাৎ থেমে যায় বা গণণা করতে অসমর্থ হয়) তা নির্ণয় করতে পারে। একইভাবে,
২)বাস্তবে কোন মেশিন অবস্থান করে কিনা যে তার ফিতের উপর কোন কাল্পনিক মেশিন প্রদত্ত চিহ্ন ছাপতে কখনো সক্ষম তা নির্ণয় করতে পারে।

এভাবে তিনি সরল যন্ত্রের কাল্পনিক গণণার গাণিতিক ধারণা দিয়ে গণণার ধর্ম সাধারণভাবে প্রমাণ করতে পারলেন- সরলভাষায় সিদ্ধান্ত নির্ণায়ক সমস্যার (Entscheidungs Problem) সমাধান করলেন।

টুরিং মেশিনের বর্ণণা 

১) একটা অসীম বিস্তৃত ফিতে পর পর ছোট ছোট ঘরে বিভক্ত। ফিতের সসীম অংশে প্রতিটি ঘর একটা করে অক্ষর ধারণ করে থাকে। অসীম অংশের ঘরগুলি ফাঁকা হিসাবে ধরা হয় (যা ০ চিহ্ন দিয়ে চিহ্নিত করা হয়)।
২) একটা যন্ত্র যে একবারে ফিতের উপর চিহ্ন পড়তে বা লিখতে পারে বা বাম/ ডান দিকের ঘরে সরতে পারে। কোন কোন মডেলে যন্ত্র সরতে পারে আর ফিতেটা স্থির থাকে।

কোয়াণ্টাম কম্পিউটারের ধারণা

সাল ১৯৭০। আমেরিকান বিজ্ঞানী পল এ বেনিওফ  (Paul A Benioff)  ‘স্ক্রোডিঙ্গার সূত্র’ (Schordinger equation)- এর সাহায্যে কোয়াণ্টাম গণণার তাত্ত্বিক বাস্তবতা নিয়ে গবেষণা শুরু করলেন। তিনি টুরিং মেশিনের কোয়াণ্টাম মেকানিকাল (Quantum Mechanical) ব্যাখ্যা দিলেন যা ১৯৮০ সালে প্রকাশিত হয়। এভাবে জন্ম নিল এক নতুন বিষয়-কোয়াণ্টাম গণণা বিদ্যা (Quantum Computing)। তিনি তাঁর গবেষণার মাধ্যমে তত্ত্বগত দিক থেকে প্রথম কোয়াণ্টাম কম্পিউটার গড়ে তোলার সম্ভাবনা সকলের সামনে তুলে ধরলেন। পরে রিচার্ড ফেম্যান ও ইউরি ম্যানিন ধারণা দিলেন, কোয়াণ্টাম কম্পিউটার দ্বারা প্রথাগত কম্পিউটারে অমীমাংসিত গণণার সয়াধান সম্ভব।১৯৯৪ সালে পিটার সোর, সোর অ্যাল্গোরিদিমের সাহায্যে কোয়াণ্টাম ভাষা আদানপ্রদানের মাধ্যম গড়ে তুললেন। কিন্তু এতদস্বত্তেও কম্পিউটার জগতে গবেষকদের কাছে কোয়াণ্টাম কম্পিউটার গড়ে তোলা ছিল স্বপ্নাতীত কল্পনা মাত্র।

সাধারণ কম্পিউটারে তথ্য সরবরাহ করা হয় বাইনারি ডিজিট বা বিটস দ্বারা। একটা বিট হল কম্পিউটারে তথ্য সরবরাহের একক। তেমনি কোয়াণ্টাম বিটস বা কিউবিটস হল কোয়াণ্টাম তথ্য সরবরাহের একক। প্রথাগতভাবে কম ডিসি ভোল্টেজ-এর দুই বিভবের যে কোন একটিকে বিট হিসাবে ধরা হয়।বিট চিহ্নিত হয় ০ বা ১ দ্বারা। তবে কিউবিট মাপা হয় ।০> (কেট জিরো) বা ।১> (কেট ওয়ান) দ্বারা। আবার কিউবিট একই সময়ে ০ বা ১ যুগ্ম অবস্থান নিতে পারে। এই অবস্থাকে বলা হয় ‘Super position’ বা ‘উপরিপাতন’। বিজ্ঞানের ভাষায় এই উপরিপাতন বা কোয়াণ্টাম সুপার পজিশন (অনেকটা পদার্থবিদ্যার কম্পনের মতোই) যে কোন দুটি কোয়াণ্টাম অবস্থা (বা তার বেশি)পরষ্পর মিলিত হয়ে অন্য একটি কোয়াণ্টাম অবস্থার জন্ম দেয়। আবার অন্যভাবে বলতে গেলে কোন একটি কোয়াণ্টাম অবস্থা অনেকগুলি কোয়াণ্টাম অবস্থার সমষ্টী।

একটা উদাহরণ দিলে ব্যাপারটা পরিষ্কার হবে। ধরা যাক, আমাদের কাছে ৩০ টা ০ আর ৩০ টা ১ এর ক্রম সজ্জা আছে যা থেকে ১০০ কোটি সম্ভাব্য মাণ আশা করা যায়। সেক্ষেত্রে কোন একক সময়ে একটি সাধারণ কম্পিউটার ১০০ কোটি মাণের মধ্যে শুধু মাত্র কোন একটি অবস্থাকে নির্দেশ করতে পারে কিন্ত কোয়াণ্টাম কম্পিউটার একক সময়ে একই সাথে ১০০ কোটি সম্ভাব্য মাণের কোয়াণ্টাম সমাহারকে নির্দেশ করবে। অন্যভাবে বলতে গেলে, ১০০ কোটি সম্ভাব্য মাণের তথ্য নির্ধারনের ক্ষেত্রে একই সময়ে ভিন্ন ভিন্ন গণণার জন্য যদি সাধারণ কম্পিউটার সমান্তরালভাবে চালানো হয়, তবে একই সময়ে ১০০ কোটি প্রসেসর সম্পণ্ণ সাধারণ কম্পিউটারের প্রয়োজন। সেক্ষেত্রে কোয়াণ্টাম কম্পিউটার একই সময়ে একটিমাত্র হার্ডওয়ারের সাহায্যে ১০০ কোটি কম্পিউটারের কাজ করতে সক্ষম। এবং সম্ভাব্য ফলাফল একটাই আসবে এবং সেক্ষেত্রে বাকি ৯৯,৯৯,৯৯,৯৯৯ সম্ভাব্য মানের ফলাফল পরষ্পর জুড়ে মিলিয়ে যাবে।

এই কিউবিটস (Qubits) এর অন্যতম বৈশিষ্ট্য হল অন্য কিউবিটসকে প্রভাবিত করা, যা সাধারণ বিটস এর ক্ষেত্রে ঘটে না। এক্ষেত্রে কিউবিটস একই সাথে উৎপন্ন হয়, পরষ্পর মিলিত হয় এবং খুব সন্নিবিষ্ট ভাবে অবস্থান করে, স্বাধীনভাবে সেই কিউবিটসের অবস্থান ব্যাখ্যা করা সম্ভব নয়। এই ঘটনাকে বলে ‘কিউবিটস জট’ বা ‘Qubits Entanglement’।

একটা পরীক্ষামূলক উদাহরণের সাহায্যে কিউবিটসের ধারণা আমরা পরিষ্কার করতে পারি। ধরা যাক, একটা দুই টাকার কয়েনকে টেবিলে খাঁড়া ভাবে রেখে লাট্টুর মতো ঘোরানো হল। খাঁড়া অবস্থায় যখন লাট্টুর মতো ঘোরার সময় আমরা কিন্তু কোন ক্ষেত্রেই কয়েনের কোন একটি নির্দিষ্ট পিঠের অবস্থানকে নির্ণয় করতে পারব না, বরং সমগ্র অংশকে একসাথে দেখব। অন্যভাবে বলতে গেলে দুটি পিঠের অবস্থানের উপরিপাতন ঘটে। এবার কয়েনের এক পিঠ ।০> (কেট জিরো) আর অন্য পিঠ ।১> (কেট ওয়ান) কল্পনা করলাম। এখন ঘুর্ণণের সময় যে রকম পিঠগুলো আলাদা করে দেখা যায় না, কিউবিটসগুলো ঠিক তেমনি উপরি পাতনের ফলে মিশ্র অবস্থান লাভ করে এবং নিরবিচ্ছিন্ন ধারায় তথ্য সরবরাহ করে।
নিচে ছবি দিয়ে সাধারণ বিট (Classical Bits) ও কিউবিটের তফাত দেখানো হল।

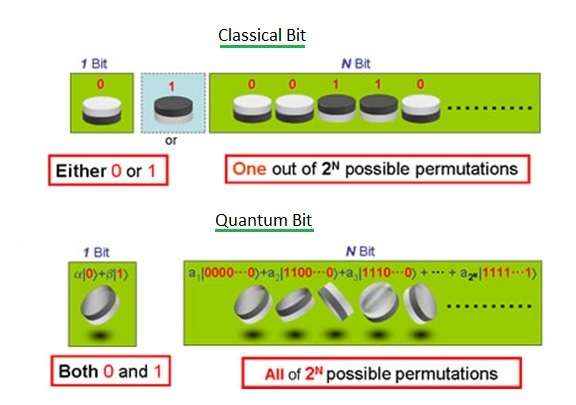
অর্থাৎ, একটা কিউবিটকে ।০> ও ।১> এর সরলরৈখিক যুগ্ম অবস্থান দ্বারা বর্ণণা করা সম্ভব।

গাণিতিক পরিভাষায়

                    |¥>= α|0>+β|1>

যেখানে, |¥> = কিউবিটসের উপরিপাতনের সম্ভাবনাময় বিস্তার

       α ও β = সম্ভাবনাময় বিস্তার এবং সাধারণ অবস্থায় জটিল রাশি।

      α|0>+β|1> = সম্ভাবনাময় উপরিপাতনের সমষ্টী

 আমরা যদি সাধারণ অবস্থায় দেখি, তবে ‘বর্ণ’ ( Born’s principle) এর নিয়ম অনুযায়ী । α।² হল ।০> র সম্ভাবনাময় ফল যার মাণ ০ এবং । β ।² হল ।১> র সম্ভাবনাময় ফল যার মাণ 1।
সেক্ষেত্রে,

। α।² + । β ।² = 1

এখানে উপরিপাতনের অবস্থায় ০ বা 1 কোন মানই আমরা পাই না, তবে কিউবিটের । α।² এর সম্ভাবনাময় মাণ ০ এবং । β ।² এর সম্ভাবনাময় মাণ 1 হয়।

একটা কিউবিটসের উপরিপাতনের সম্ভাবনাময় বিস্তারকে ব্লক  গোলকের  (Bloch Sphere) সাহায্যে দেখানো যেতে পারে।
   
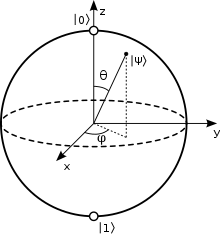
               ব্লক গোলক