- হরিদাস পাল আলোচনা বিজ্ঞান ও প্রযুক্তি

-
হিগস বোসনের গল্প - ২
অনির্বাণ কুণ্ডু লেখকের গ্রাহক হোন
আলোচনা | বিজ্ঞান ও প্রযুক্তি | ০৫ মার্চ ২০২৪ | ১৭৪৬ বার পঠিত | রেটিং ৪.৯ (৭ জন) - ফিজিক্স ক্লাস - ১ | ফিজিক্স ক্লাস - ২ | ফিজিক্স ক্লাস - ৩ | ফিজিক্স ক্লাস - ৪ | ফিজিক্স ক্লাস - ৫ | ফিজিক্স ক্লাস - ৬ | ফিজিক্স ক্লাস - ৭২০১২ সালের চৌঠা জুলাই সার্নের বিজ্ঞানীরা হিগস বোসন আবিষ্কারের কথা ঘোষণা করেন। তার কিছুদিনের মধ্যেই পশ্চিমবঙ্গ বিজ্ঞানমঞ্চের পক্ষ থেকে হিগস বোসন নিয়ে একটি ছোট পুস্তিকা প্রকাশ করা হয়। এই লেখাটি সেই পুস্তিকায় স্থান পেয়েছিল, তার জন্যে সম্পাদকমণ্ডলীকে আন্তরিক ধন্যবাদ। তারপরে প্রায় এক যুগ, অর্থাৎ বারো বছর কেটে গেছে। হিগস বোসনের আবিষ্কার এখন কণা পদার্থবিদ্যার পাঠ্যবইয়ে জায়গা করে নিয়েছে। লেখাটি যতদূর পারা যায়, অপরিবর্তিত রাখা হল। কিছু অপ্রয়োজনীয় জিনিস বাদ গেছে, কিছু নতুন তথ্য ঢুকেছে। বাঁকা হরফ বা ইটালিক্সে যা লেখা হয়েছে, সেগুলো নতুন সংযোজন।
৫
একশো বছরেরও বেশি আগে আইনস্টাইন দেখিয়ে গিয়েছিলেন যে কোনো কণার মোট শক্তির দুটো অংশ আছে, একটা আসে তার ভর থেকে, আর একটা কণা চললে তার ভরবেগ থেকে (লম্বকর্ণের উদাহরণ মনে করুন)। কণা যদি স্থির থাকে, তাহলে তার মোট শক্তি ভরের সমানুপাতিক ভরকে আলোর বেগের বর্গ দিয়ে গুণ করলে শক্তি পাওয়া যায়। এটাই সেই বিখ্যাত E = m c2 ফরমুলা। বিজ্ঞানীরা সেইজন্যে এখন কণার ভরকেও শক্তির এককে প্রকাশ করেন। এর পরের আলোচনায় যেতে হলে এই এককটাকে একটু বুঝে নিতে হবে।
স্কুলে পড়েছিলেন – শক্তির একক জুল বা তার এক কোটি ভাগের এক ভাগ, আর্গ। মৌলিক কণাদের জগতে জুল বা আর্গ দুটোই বড্ড বড়ো একক। আমরা ইলেকট্রন-ভোল্ট বলে একটা একক ব্যবহার করি। একটা এক ভোল্টের ব্যাটারির দু-প্রান্ত যদি দুটো ধাতব পাতের সঙ্গে লাগিয়ে দেওয়া যায়, তাহলে একটা ইলেকট্রন সেই পাতদুটোর মধ্যে দিয়ে গেলে যতটুকু অতিরিক্ত শক্তি পাবে – সেটাই এক ইলেকট্রন-ভোল্ট। মোটামুটিভাবে একের পিঠে উনিশটা শূন্য বসালে যা হয়, তত ইলেকট্রন-ভোল্টে এক জুল, কাজেই একক হিসেবে দৈনন্দিন জীবনে ব্যবহারের পক্ষে এটা ভারি ছোটো। বিজ্ঞানীরা ইলেকট্রন-ভোল্টের অনেকগুলো গুণিতকও ব্যবহার করেন – কিলো বা ১০০০, মেগা বা ১০০০,০০০, গিগা বা ১০০০,০০০,০০০। এর পরেও আছে, সেগুলো না জানলেও চলবে। একটা হাইড্রোজেন পরমাণুর ইলেকট্রনকে তাড়িয়ে বের করে দিতে ১৩.৬ ইলেকট্রন-ভোল্ট শক্তি লাগে। যখন বলি, একটা ইলেকট্রনের ভর ০.৫১১ মেগা ইলেকট্রন-ভোল্ট, বা একটা প্রোটনের ভর ৯৩৮ মেগা ইলেকট্রন-ভোল্ট, তার মানে হল ওদের ভরকে আলোর বেগের বর্গ দিয়ে গুণ করলে ঐ পরিমাণ শক্তি পাওয়া যাবে।
তড়িৎচুম্বকীয় বল এক জায়গা থেকে আর এক জায়গায় বয়ে নিয়ে যায় ফোটন। ফোটনের কোনো ভর নেই, তার শক্তির পুরোটাই চলার শক্তি। ফোটনের যে ভর নেই – এটা কিউইডির পক্ষে আশীর্বাদ—ভর থাকলে তত্ত্বটা তৈরি করাই যেত না। কেন যেত না, সেটা এখানে বোঝাবার চেষ্টা করাটা একটু গুরুগম্ভীর হয়ে যাবে, আর আমরা তো অঙ্ক যতটা পারা যায় এড়িয়ে যেতে চাইছি, সুতরাং এই কথাটা আপাতত মেনে নিন, যে, কিউইডির কাঠামোর একটা মূল উপাদান—প্রধান উপাদান বললেও অত্যুক্তি হবে না—ফোটনের ভরশূন্যতা। মহাকর্ষের কোনো কোয়ান্টাম তত্ত্ব আমরা এখনো পাইনি, যদি কোনোদিন পাই—মহাকর্ষ বল যে কণা বয়ে নিয়ে যায় (পাওয়ার অনেক আগে থেকেই এর নাম ঠিক হয়ে আছে, গ্র্যাভিটন), তারও ভর শূন্য হতে হবে। এদের ভর শূন্য বলেই তড়িৎচুম্বকীয় বল বা মহাকর্ষের প্রভাব বহুদূরেও অনুভব করা যায়।
এতক্ষণ সব কিছু বেশ চমৎকার চলছিল, কিন্তু এইবার ক্ষীণ বলের কোয়ান্টাম তত্ত্ব বানাতে গিয়ে বিজ্ঞানীরা পড়লেন বিপদে। ক্ষীণ বলের প্রকৃতি একটু আলাদা, তাকে বয়ে নিয়ে যেতে গেলে একটা কণা দিয়ে হয় না—তিনটে কণা লাগে—বিপদ সেটা নয়। একটা কণার জন্যে যদি তত্ত্ব তৈরি করতে পারা যায়, তাহলে তিনটে কণার জন্যেও যায়, শুধু অঙ্কটা একটু জটিল হবে এই যা। এই সব কণাই ফোটনের জাতভাই, সবাই বসু-আইনস্টাইনের সংখ্যায়ন মেনে চলে। মুশকিল এই যে ক্ষীণ বল মোটেই তড়িৎচুম্বকীয় বলের মতন বহুদূর পর্যন্ত ছড়িয়ে পড়ে না, তার মসজিদ বড়োজোর পরমাণুর নিউক্লিয়াস—তার পরে আর ক্ষীণ বলের কোনো প্রভাব টের পাওয়া যায় না। এর কারণও লুকিয়ে আছে কোয়ান্টাম তত্ত্বের মধ্যেই; কোয়ান্টাম তত্ত্বের সবচেয়ে বড়ো স্তম্ভ হিসেবে যাকে দেখা হয়, সেই হাইজ়েনবার্গের অনিশ্চয়তা নীতির মধ্যে। সেই কারণটা হল, এই তিনটে ক্ষীণ বলের ‘ফোটন’—কেউই ভরশূন্য নয়। এদের প্রত্যেকেরই ভর আছে, এবং সেটাও বেশ ভালো রকম, ৮০-৯০ গিগা ইলেকট্রন-ভোল্টের মতন। অর্থাৎ একটা প্রোটনের থেকে এরা প্রায় একশো গুণ ভারি। কিউইডির মতন তত্ত্ব বানাতে গেলে এদের ভরটা কীভাবে দেওয়া যাবে?৬ 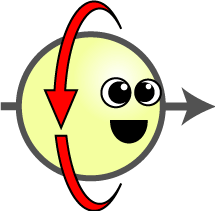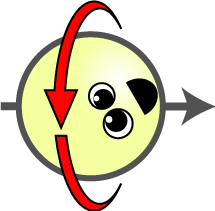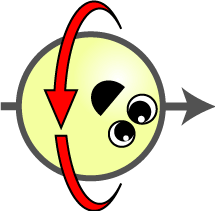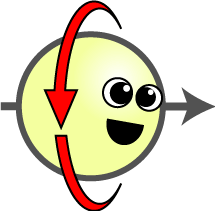 মনে করুন, একটা বল নিজের অক্ষের উপর ঘুরতে ঘুরতে এগিয়ে চলেছে। আপনি বলটার পিছনে দাঁড়িয়ে তার এগিয়ে যাওয়া দেখছেন। বলের গায়ে যদি একটা ফুটকি দেওয়া থাকে, তাহলে আপনি দেখবেন এই ফুটকিটা স্প্রিংয়ের মতো প্যাঁচানো কক্ষপথে এগিয়ে চলেছে। এই স্প্রিংটা, ঘড়ির কাঁটা যেদিকে ঘোরে—সেদিকে—অর্থাৎ দক্ষিণাবর্তে (পাশের ছবি) ঘুরতে পারে, আবার ঘড়ির কাঁটার বিপরীতে, অর্থাৎ বামাবর্তেও ঘুরতে পারে।
মনে করুন, একটা বল নিজের অক্ষের উপর ঘুরতে ঘুরতে এগিয়ে চলেছে। আপনি বলটার পিছনে দাঁড়িয়ে তার এগিয়ে যাওয়া দেখছেন। বলের গায়ে যদি একটা ফুটকি দেওয়া থাকে, তাহলে আপনি দেখবেন এই ফুটকিটা স্প্রিংয়ের মতো প্যাঁচানো কক্ষপথে এগিয়ে চলেছে। এই স্প্রিংটা, ঘড়ির কাঁটা যেদিকে ঘোরে—সেদিকে—অর্থাৎ দক্ষিণাবর্তে (পাশের ছবি) ঘুরতে পারে, আবার ঘড়ির কাঁটার বিপরীতে, অর্থাৎ বামাবর্তেও ঘুরতে পারে।
ইলেকট্রন, নিউট্রিনো, কোয়ার্ক – এইরকম সমস্ত ফের্মিয়নেরও দক্ষিণাবর্তী এবং বামাবর্তী – এই দু-রকম চেহারা আছে। এরা অবশ্য বিন্দু কণা, কাজেই তারা নিজের অক্ষের উপর ঘোরে এটা বলা অর্থহীন—বিন্দুর আবার অক্ষ কী (এখনো অনেক পাঠ্যবই বা জনপ্রিয় বিজ্ঞানের বইতে এমনভাবেই বলা থাকে, যেন ইলেকট্রন আর ফুটবলের কোনো তফাৎ নেই। ইলেকট্রনের এই তথাকথিত “ঘোরা”র সঙ্গে আহ্নিক গতি মেলাতে যাবেন না)? ঠিক কী বলতে চাইছি, সেটা বুঝতে গেলে কোয়ান্টাম তত্ত্বের একটু গভীরে যেতে হবে, সুতরাং এখানে আমরা সেই চেষ্টাটা করবো না। মোট কথা হল, এই ফের্মিয়ন কণাগুলোকে দু-ভাগে ভাগ করা যায়।
দুটি বিপরীত দিকে গতিশীল বামপন্থী কণা হঠাৎ এইরকম ভাগ করাটা দরকার হল কেন? ম্যাক্সওয়েলের তত্ত্ব বলি, বা কিউইডি—সেখানে ইলেকট্রন হল ইলেকট্রন, তার দু-রকম শ্রেণীবিভাগ তো করি না। তার কারণ হল ফোটনের প্রকৃতি। ফোটনের আমরা-ওরা নেই, তার কাছে দক্ষিণ আর বাম সব ইলেকট্রনই সমান। তড়িৎচুম্বকীয় তত্ত্ব দিয়ে এই দু-রকম ইলেকট্রনকে কোনোভাবেই আলাদা করা যায় না। আলাদা যে করা যায় না, সেটাও কিউইডির অঙ্কের মধ্যেই খুব সুন্দরভাবে গুছিয়ে রাখা আছে। ক্ষীণ বলের ব্যাপারটা একটু অন্যরকম। গত শতাব্দীর পঞ্চাশের দশকের গোড়ায় মহাজাগতিক রশ্মির উপর করা কিছু পরীক্ষা থেকে কোনো কোনো বিজ্ঞানীর সন্দেহ হয়, যে, ক্ষীণ বল দক্ষিণ আর বাম কণাকে একই চোখে দেখে না। প্রথম এই কথাটা বলেন সাং-দাও লি এবং চেন-নিং ইয়াং নামে দুই চৈনিক-আমেরিকান বিজ্ঞানী। পরীক্ষা করে মাদাম চিয়েন-শিয়ং য়ু এবং তাঁর সহকর্মীরা দেখান, যে, ক্ষীণ বলের টান বামপন্থী কণাদের দিকে বেশি। মরিস গোল্ডহেবার ও তাঁর সহকর্মীরা আরো এক ধাপ এগিয়ে দেখান, যে, ক্ষীণ বল শুধু বামপন্থী কণাদেরই চোখে দেখে, দক্ষিণপন্থীদের দেখতেই পায় না। এ ব্যাপারে নিউট্রিনোর কথা বলা যেতে পারে। নিউট্রিনোর কোনো তড়িৎ আধান নেই, কাজেই তার উপর তড়িৎচুম্বকীয় বল কাজ করে না। নিউট্রিনোর উপর কাজ করে শুধু ক্ষীণ বল, আর সে বামপন্থী ছাড়া কাউকে দেখতেই পায় না, সুতরাং দক্ষিণপন্থী নিউট্রিনো বলে কিছু হয়ই না। মহাবিশ্ব জুড়ে যত নিউট্রিনো, সকলেই বাম। ক্ষীণ বলের চেহারাটা ঠিক কীরকম, সেটা অঙ্ক কষে দেখান ১৯৫৭ সালে রবার্ট মার্শাক ও ভারতীয় বিজ্ঞানী জর্জ সুদর্শন, এবং ১৯৫৮তে রিচার্ড ফাইনম্যান ও মারে গেলমান। সুদর্শন নিঃসন্দেহে স্বাধীনতা-উত্তর সময়ের সেরা ভারতীয় তাত্ত্বিক পদার্থবিদ, কিন্তু আমরা খুব কম জনেই তাঁর নাম জানি, বোধহয় জীবনের বেশিরভাগ সময়টা আমেরিকায় কাটানোর জন্যেই।
হঠাৎ এইরকম ভাগ করাটা দরকার হল কেন? ম্যাক্সওয়েলের তত্ত্ব বলি, বা কিউইডি—সেখানে ইলেকট্রন হল ইলেকট্রন, তার দু-রকম শ্রেণীবিভাগ তো করি না। তার কারণ হল ফোটনের প্রকৃতি। ফোটনের আমরা-ওরা নেই, তার কাছে দক্ষিণ আর বাম সব ইলেকট্রনই সমান। তড়িৎচুম্বকীয় তত্ত্ব দিয়ে এই দু-রকম ইলেকট্রনকে কোনোভাবেই আলাদা করা যায় না। আলাদা যে করা যায় না, সেটাও কিউইডির অঙ্কের মধ্যেই খুব সুন্দরভাবে গুছিয়ে রাখা আছে। ক্ষীণ বলের ব্যাপারটা একটু অন্যরকম। গত শতাব্দীর পঞ্চাশের দশকের গোড়ায় মহাজাগতিক রশ্মির উপর করা কিছু পরীক্ষা থেকে কোনো কোনো বিজ্ঞানীর সন্দেহ হয়, যে, ক্ষীণ বল দক্ষিণ আর বাম কণাকে একই চোখে দেখে না। প্রথম এই কথাটা বলেন সাং-দাও লি এবং চেন-নিং ইয়াং নামে দুই চৈনিক-আমেরিকান বিজ্ঞানী। পরীক্ষা করে মাদাম চিয়েন-শিয়ং য়ু এবং তাঁর সহকর্মীরা দেখান, যে, ক্ষীণ বলের টান বামপন্থী কণাদের দিকে বেশি। মরিস গোল্ডহেবার ও তাঁর সহকর্মীরা আরো এক ধাপ এগিয়ে দেখান, যে, ক্ষীণ বল শুধু বামপন্থী কণাদেরই চোখে দেখে, দক্ষিণপন্থীদের দেখতেই পায় না। এ ব্যাপারে নিউট্রিনোর কথা বলা যেতে পারে। নিউট্রিনোর কোনো তড়িৎ আধান নেই, কাজেই তার উপর তড়িৎচুম্বকীয় বল কাজ করে না। নিউট্রিনোর উপর কাজ করে শুধু ক্ষীণ বল, আর সে বামপন্থী ছাড়া কাউকে দেখতেই পায় না, সুতরাং দক্ষিণপন্থী নিউট্রিনো বলে কিছু হয়ই না। মহাবিশ্ব জুড়ে যত নিউট্রিনো, সকলেই বাম। ক্ষীণ বলের চেহারাটা ঠিক কীরকম, সেটা অঙ্ক কষে দেখান ১৯৫৭ সালে রবার্ট মার্শাক ও ভারতীয় বিজ্ঞানী জর্জ সুদর্শন, এবং ১৯৫৮তে রিচার্ড ফাইনম্যান ও মারে গেলমান। সুদর্শন নিঃসন্দেহে স্বাধীনতা-উত্তর সময়ের সেরা ভারতীয় তাত্ত্বিক পদার্থবিদ, কিন্তু আমরা খুব কম জনেই তাঁর নাম জানি, বোধহয় জীবনের বেশিরভাগ সময়টা আমেরিকায় কাটানোর জন্যেই।
ক্ষীণ বলের এই চেহারাটা বের করার পর সমস্যা দেখা দিল। বাকি সব ঠিক আছে, কিন্তু যে সব ফের্মিয়নের উপর ক্ষীণ বল কাজ করে (অর্থাৎ সমস্ত জানা মৌলিক ফের্মিয়নের উপর—ক্ষীণ বলের প্রভাব কেউই এড়াতে পারে না) তাদের ভর শূন্য হতেই হবে। ইলেকট্রন, কোয়ার্ক – এদের ভর থাকলে ক্ষীণ বলের তত্ত্বটা আর লেখা যাবে না। নিউট্রিনোর ভর নেই বলেই ধরে নেওয়া যেতে পারে (আমরা এখন জানি এটাও পুরোপুরি সত্যি নয়—নিউট্রিনোর ভর আছে—যদিও বাকি মৌলিক কণাদের তুলনায় অনেক কম) সুতরাং তাদের জন্য সমস্যাটা মুলতুবি রাখলেও রাখা যায়, অন্যদের বেলায় কী হবে?
তার মানে ব্যাপারটা এইরকম দাঁড়াল – ক্ষীণ বল যারা বয়ে নিয়ে যায় তাদের ভর আছে, কিন্তু সেই ভর কী করে দেওয়া যাবে জানি না। যাদের উপর ক্ষীণ বল কাজ করে, অর্থাৎ ইলেকট্রন জাতীয় কণা, তাদেরও ভর আছে, কিন্তু সেটাও দেওয়ার কোনো রাস্তা নেই। তার মানে ক্ষীণ বল আর ভর, দুটো জিনিস একসঙ্গে থাকতে পারে না, অথচ দুটোই যে আছে সে নিয়ে তো কোনো সন্দেহ নেই। এর চেয়ে বড়ো চ্যালেঞ্জ আর কী হতে পারে?৭ 
সূত্র: উইকি)
প্রতিসাম্য কাকে বলে, সে সম্বন্ধে স্কুলেই আমাদের অল্পবিস্তর ধারণা হয়। গাছের পাতা বা আমাদের চেহারা মাঝ বরাবর প্রতিসম, বৃত্ত বা গোলক সম্পূর্ণ প্রতিসম। প্রতিসাম্যের ধারণাটা খুব জরুরি। গোল টেবিলকে শুধুমাত্র একটা পায়ার উপর দাঁড় করাতে গেলে পায়াটা যে টেবিলের কেন্দ্র দিয়ে যেতে হবে—সে কথা সকলেই জানে। আপনাকে না দেখেও জুতোর দোকানদার আপনার দু-পায়ের জুতো একই মাপে বানায়।
প্রতিসাম্য যে সবসময়েই অটুট থাকে তা নয়। আপনার বাঁ-পকেটে যদি একটা কলম গুঁজে দেওয়া হয়, বা ডান হাতে একটা থলে ধরিয়ে দেওয়া হয়, তা হলে আপনি আর মাঝ-বরাবর প্রতিসম থাকবেন না। পৃথিবী প্রতিসম নয়, তার কারণ মহাদেশ ও মহাসাগরগুলোর চেহারা আলাদা। এটাকে আমরা জোর করে প্রতিসাম্য ভেঙে দেওয়া বলতে পারি। তড়িৎচুম্বকীয় বল দক্ষিণ ও বাম ইলেকট্রনের জন্য প্রতিসম, কিন্তু ক্ষীণ বল নয়।
আর একভাবে প্রতিসাম্য ভাঙতে পারে। ধরুন, আপনারা জনা দশেক মিলে একটা রেস্টুরেন্টে খেতে গেছেন। ওয়েটার একটা গোল টেবিলে বসালো—সবার থেকে সবাই সমান দূরত্বে—একেবারে নিখুঁত প্রতিসাম্য। তারপর দশটা গেলাস এনে টেবিলে রেখে দিয়ে গেল, দু-জনের ঠিক মাঝখানে একটা করে গেলাস। আবারও প্রতিসম। এখন আপনি ডান হাতের গেলাস তুলবেন, না বাঁ হাতের – সেটা আপনার মর্জি। কেউ না কেউ তো প্রথম গেলাসটা তুলবেনই, যাঁর সবচেয়ে বেশি তেষ্টা পেয়েছে, তিনিই প্রথম তুলবেন। যেই তিনি কোনো একটা গেলাস তুললেন – ধরা যাক ডান হাতের, প্রতিসাম্য ভেঙে গেল। ওয়েটার কিন্তু জোর করে প্রতিসাম্য ভাঙেনি, আপনাদেরই একজন ভাঙলেন। তাঁর হাতে দুটো সমান সম্ভাবনা ছিল – ডান বা বাঁ দিকের গেলাস তোলার, তিনি যে কোনো একটা বেছেছেন। কিন্তু যেই তিনি ডানদিকের গেলাস তুললেন, আপনাদের সবাইকেই ডানদিকের গেলাসই তুলতে হবে, নইলে কেউ একজন গেলাস না পেয়ে রেগে যাবেন আবার কেউ দুটো গেলাস নিয়ে বোকাবোকা মুখ করে বসে থাকবেন। অর্থাৎ আপনাদের সবারই দুটো অবস্থায় যাওয়ার সমান সম্ভাবনা ছিল, আপনারা নিজে থেকে যে কোনো একটা অবস্থায় গেছেন।
কোনো পাত্রে জল থাকলে তার নির্দিষ্ট কোনো দিক নেই, কিন্তু জল জমে যেই বরফ হবে, বরফের কেলাসের একটা নির্দিষ্ট অক্ষ থাকবে। আবারও সেই একই ব্যাপার—গোড়ায় প্রতিসাম্য ছিল, কিন্তু নিজে থেকে সেটা ভেঙে গেল। এটাকে আমরা বলব প্রতিসাম্যের স্বতঃস্ফূর্ত ভাঙন।
পঞ্চাশের দশকের মাঝামাঝি শুইংগার প্রথম আলোচনা করেন কীভাবে ক্ষীণ বলের তত্ত্বকে কিউইডির ছাঁচে ফেলা যেতে পারে। ১৯৬১ সালে শেলডন গ্ল্যাশো এই অঙ্কটা আরো গুছিয়ে করে দেখান। যদিও কেউই ক্ষীণ ফোটন তিনটের ভর কীভাবে আসতে পারে—সে সম্বন্ধে কিছু বললেন না, শুধু ভর আছে এটা ধরে নিলেন। মুশকিল হল, এটা জোর করে ধরে নিলে কিউইডির একটা বড়ো ধর্ম নষ্ট হয়ে যায় – সেটা হল, একবার গোটা তিনেক জায়গা থেকে অসীমকে তাড়িয়ে দিলে আর কোথাও কখনো অসীম না আসা। আর অঙ্ক করতে গিয়ে বারবার অসীম উত্তর এলে, তা দিয়ে কাজ করা প্রায় অসম্ভব। অর্থাৎ এখনো কোথাও বড়ো একটা ফাঁক থেকে যাচ্ছে।৮ 
বাঁদিকের উপরের কোণা থেকে ঘড়ির কাঁটার দিকে: আংলেয়ার, ব্রাউট, কিবল, হিগস, হ্যাগেন, গুরালনিক
১৯৬৪ সালে ছ-জন বিজ্ঞানী তিনখানা ঐতিহাসিক প্রবন্ধ লিখলেন (১৯৬৪কে কণা-পদার্থবিদ্যার ইতিহাসে বলে অ্যানাস মিরাবিলিস অর্থাৎ অলৌকিকের বছর – ঐ বছরে অনেকগুলো অসাধারণ কাজ একইসঙ্গে ঘটেছিল)। এই ছ-জন বিজ্ঞানী হলেন ফ্রাঁসোয়া আংলেয়ার ও রবার্ট ব্রাউট, পিটার হিগস, এবং জেরাল্ড গুরালনিক, রিচার্ড হ্যাগেন, ও টমাস কিবল। এঁদের মধ্যে ব্রাউট, গুরালনিক আর কিবল এখন আর আমাদের মধ্যে নেই (প্রথম যখন লেখাটি প্রকাশিত হয়, গুরালনিক ও কিবল তখনো বেঁচে ছিলেন, তার কিছুদিন আগেই কিবল কলকাতায় বক্তৃতা দিয়ে গেছেন)।
এঁরা ঠিক কী করেছিলেন—সেটা বুঝতে গেলে আগে ক্ষেত্র সম্বন্ধে আমাদের ধারণাটা একটু ঝালিয়ে নেওয়া দরকার। এ ক্ষেত্র মানে মাঠ নয়। তড়িৎক্ষেত্র, চৌম্বকক্ষেত্র, বা মহাকর্ষের ক্ষেত্রের কথা স্কুলে বিজ্ঞানের বইতে আমরা পড়েছি। এই সব ক্ষেত্রের মধ্যে কোনো কণা থাকলে তা একটা বল অনুভব করে। ম্যাক্সওয়েলের পরে তড়িৎ ও চৌম্বক ক্ষেত্রকে আলাদা করার কোনো মানে হয় না, আমরা একসঙ্গে তড়িৎচৌম্বক ক্ষেত্রের কথা বলতে পারি। কোয়ান্টাম তত্ত্ব বলে, এই সব ক্ষেত্রের সঙ্গে একটা করে কণা জড়িয়ে থাকে, যেমন ফোটন বা এখনো না পাওয়া গ্র্যাভিটন। শুধু তাইই নয়। ফোটন ও ইলেকট্রনের মধ্যে সংখ্যায়নের হিসেবটা ছাড়া এমন বিশেষ কিছু তফাৎ নেই—দু-জনেরই কণা ও তরঙ্গ – দুটো করে সত্তা আছে। সুতরাং ইলেকট্রনের জন্যেও এইরকম একটা ক্ষেত্রের কথা ভাবা যেতে পারে।
হিগসরা দেখাতে চেয়েছিলেন, কিউইডির ভালো দিকগুলোকে নষ্ট না করে ফোটন জাতীয় ভরশূন্য কণাকে ভর দেবার কোনো রাস্তা আছে কিনা। তাঁরা একটা বিশেষ রকমের ক্ষেত্র কল্পনা করলেন। এর আগে আমরা ইলেকট্রনের দু-রকম চলনের কথা দেখেছি – দক্ষিণাবর্তী ও বামাবর্তী । ফোটনেরও এই দু-রকম চলন আছে, আসলে থাকা উচিত ছিল তিনরকম, কিন্তু ফোটন ভরশূন্য বলে একটা চলন বাদ পড়ে যায় (ভরযুক্ত ক্ষীণ ফোটনের বেলায় তিনরকম চলনই থাকে)। ফোটন বা তড়িৎচৌম্বক ক্ষেত্রের এই দু-রকম চলন পোলারয়েড কাচের চশমা ব্যবহার করলে সহজেই দেখতে পাওয়া যায়। হিগসরা যে ক্ষেত্রের কথা বললেন, তার কণা সবই এক রকম, তাদের কোনো আলাদা আবর্ত নেই।
হিগস ক্ষেত্রের প্রতিসাম্য-র স্বতঃস্ফূর্ত ভাঙন (সূত্র: উইকি)
এই হিগস ক্ষেত্রের একটা প্রতিসাম্য আছে, সেটা স্বতঃস্ফূর্তভাবে ভেঙে যায়। ওঁরা দেখালেন – এই সময়ে যদি ফোটন জাতীয় কোনো ভরশূন্য কণা সেখানে থাকে, তাহলে এই স্বতঃস্ফূর্ত ভাঙনের ফলে তা একটা ভর পায়, কিন্তু ভালো দিকটা হল, এর ফলে কিউইডি-র গুণগুলো নষ্ট হয় না। অর্থাৎ কিউইডি-র নিদান অনুযায়ীই অসীম তাড়ানো যায়। আবর্তহীন কোনো ক্ষেত্রের স্বতঃস্ফূর্ত প্রতিসাম্য ভাঙনের ফলে ফোটনজাতীয় কণাকে ভর দেবার এই প্রক্রিয়াটাকে আমরা হিগস প্রক্রিয়া বা হিগস মেকানিজ়ম বলি, যদিও এই ছ-জন বিজ্ঞানীই কৃতিত্বটার সমান অংশীদার। অনেকে এর সঙ্গে অ্যান্ডারসনের নামও উল্লেখ করে থাকেন।
ভাঙনের পরে ফোটনজাতীয় কণা তো ভর পেল, হিগস ক্ষেত্রের কী হল? এই প্রশ্নটা নিয়ে হিগস বাদে বাকি পাঁচজন কোনো কথাই বলেননি, তাঁদের কাছে হিগস মেকানিজমটাই একমাত্র আলোচ্য বিষয় ছিল। হিগস নিজে তাঁর দেড় পাতার প্রবন্ধের একেবারে শেষ লাইনে—অনেকটা লজ্জা-লজ্জা মুখ করেই যেন—বলেছেন, যে, ভাঙনের পরে হিগস ক্ষেত্রের আর প্রায় কিছুই পড়ে থাকবে না, শুধু চিহ্ন বা ধ্বংসাবশেষ হিসেবে একটা আবর্তহীন কণা পড়ে থাকতে পারে। আজ জীবনসায়াহ্নে এসে পিটার হিগস যদি নোবেল পুরস্কার পান—অবশ্যই পাওয়া উচিত—তাহলে ঐ শেষ লাইনটার জন্যেই পাবেন (বোঝাই যাচ্ছে, এই লাইনটা বারো বছর আগে লেখা। হিগস ও আংলেয়ার ২০১৩ সালে পদার্থবিদ্যায় নোবেল পেয়েছেন)। এই কণাটার কোনো তড়িৎ আধান নেই, আর আবর্তহীন বলে বসু-আইনস্টাইনের সংখ্যায়ন মেনে চলে।
আরো দু-বছর পরে এক বক্তৃতায় বেঞ্জামিন লি এই প্রক্রিয়াটার নাম দেন হিগস মেকানিজ়ম, আর ঐ পড়ে থাকা কণাটার নাম দেন হিগস বোসন।
চলবে...
পুনঃপ্রকাশ সম্পর্কিত নীতিঃ এই লেখাটি ছাপা, ডিজিটাল, দৃশ্য, শ্রাব্য, বা অন্য যেকোনো মাধ্যমে আংশিক বা সম্পূর্ণ ভাবে প্রতিলিপিকরণ বা অন্যত্র প্রকাশের জন্য গুরুচণ্ডা৯র অনুমতি বাধ্যতামূলক। লেখক চাইলে অন্যত্র প্রকাশ করতে পারেন, সেক্ষেত্রে গুরুচণ্ডা৯র উল্লেখ প্রত্যাশিত।ফিজিক্স ক্লাস - ১ | ফিজিক্স ক্লাস - ২ | ফিজিক্স ক্লাস - ৩ | ফিজিক্স ক্লাস - ৪ | ফিজিক্স ক্লাস - ৫ | ফিজিক্স ক্লাস - ৬ | ফিজিক্স ক্লাস - ৭
- মতামত দিন
-
বিষয়বস্তু*:
-
সুদীপ্ত | ০৫ মার্চ ২০২৪ ১৯:১৭529046
- যথারীতি এই পর্বটাও ভালো লাগলো! পড়ছি।
 ফোটনেরও এই দু-রকম চলন আছে, আসলে থাকা উচিত ছিল তিনরকম | 173.62.***.*** | ০৫ মার্চ ২০২৪ ১৯:৫৮529047
ফোটনেরও এই দু-রকম চলন আছে, আসলে থাকা উচিত ছিল তিনরকম | 173.62.***.*** | ০৫ মার্চ ২০২৪ ১৯:৫৮529047- এই সম্ভাব্য তৃতীয় চলনটা কি, তা জানার ইচ্ছে ছিল।
 dc | 2401:4900:2341:2ef1:8998:d349:4cae:***:*** | ০৬ মার্চ ২০২৪ ০৮:৫৫529065
dc | 2401:4900:2341:2ef1:8998:d349:4cae:***:*** | ০৬ মার্চ ২০২৪ ০৮:৫৫529065- দুটো পর্বই খুব ভালো লাগলো। হিগস মেকানিসম, হিগস ফিল্ড, আর কন্ডেনসেট নিয়ে অল্প দুয়েক কথা লেখার আছে, রাতে সময় পেলে লিখবো।
- মতামত দিন
-
বিষয়বস্তু*:
-
গুরুচণ্ডা৯-র বই দত্তক নিন
কোনোরকম কর্পোরেট ফান্ডিং ছাড়া সম্পূর্ণরূপে জনতার শ্রম ও অর্থে পরিচালিত এই নন-প্রফিট এবং স্বাধীন উদ্যোগটিকে বাঁচিয়ে রাখতে এককালীন বা ধারাবাহিক ভাবে গুরুভার বহন করুন।
- ভাটিয়ালি | টইপত্তর | বুলবুলভাজা | হরিদাস পাল | খেরোর খাতা | বই
- বুলবুলভাজা : সর্বশেষ লেখাগুলি
(লিখছেন... হীরেন সিংহরায়)
(লিখছেন... Aditi Dasgupta, হীরেন সিংহরায়, Sara Man)
(লিখছেন... হীরেন সিংহরায়, শিবাংশু, রমিত চট্টোপাধ্যায়)
(লিখছেন... )
(লিখছেন... Srimallar, .)
- হরিদাস পালেরা : যাঁরা সম্প্রতি লিখেছেন
(লিখছেন... dc, kk, দ)
(লিখছেন... bikarna, bikarna, .)
(লিখছেন... )
(লিখছেন... :|:, aranya, dc)
(লিখছেন... )
- টইপত্তর : সর্বশেষ লেখাগুলি
(লিখছেন... Srimallar)
(লিখছেন... Bratin Das)
(লিখছেন... সচ্চরিত্র, albert banerjee)
(লিখছেন... )
(লিখছেন... )
- কি, কেন, ইত্যাদি
- বাজার অর্থনীতির ধরাবাঁধা খাদ্য-খাদক সম্পর্কের বাইরে বেরিয়ে এসে এমন এক আস্তানা বানাব আমরা, যেখানে ক্রমশ: মুছে যাবে লেখক ও পাঠকের বিস্তীর্ণ ব্যবধান। পাঠকই লেখক হবে, মিডিয়ার জগতে থাকবেনা কোন ব্যকরণশিক্ষক, ক্লাসরুমে থাকবেনা মিডিয়ার মাস্টারমশাইয়ের জন্য কোন বিশেষ প্ল্যাটফর্ম। এসব আদৌ হবে কিনা, গুরুচণ্ডালি টিকবে কিনা, সে পরের কথা, কিন্তু দু পা ফেলে দেখতে দোষ কী? ... আরও ...
- আমাদের কথা
- আপনি কি কম্পিউটার স্যাভি? সারাদিন মেশিনের সামনে বসে থেকে আপনার ঘাড়ে পিঠে কি স্পন্ডেলাইটিস আর চোখে পুরু অ্যান্টিগ্লেয়ার হাইপাওয়ার চশমা? এন্টার মেরে মেরে ডান হাতের কড়ি আঙুলে কি কড়া পড়ে গেছে? আপনি কি অন্তর্জালের গোলকধাঁধায় পথ হারাইয়াছেন? সাইট থেকে সাইটান্তরে বাঁদরলাফ দিয়ে দিয়ে আপনি কি ক্লান্ত? বিরাট অঙ্কের টেলিফোন বিল কি জীবন থেকে সব সুখ কেড়ে নিচ্ছে? আপনার দুশ্চিন্তার দিন শেষ হল। ... আরও ...
- বুলবুলভাজা
- এ হল ক্ষমতাহীনের মিডিয়া। গাঁয়ে মানেনা আপনি মোড়ল যখন নিজের ঢাক নিজে পেটায়, তখন তাকেই বলে হরিদাস পালের বুলবুলভাজা। পড়তে থাকুন রোজরোজ। দু-পয়সা দিতে পারেন আপনিও, কারণ ক্ষমতাহীন মানেই অক্ষম নয়। বুলবুলভাজায় বাছাই করা সম্পাদিত লেখা প্রকাশিত হয়। এখানে লেখা দিতে হলে লেখাটি ইমেইল করুন, বা, গুরুচন্ডা৯ ব্লগ (হরিদাস পাল) বা অন্য কোথাও লেখা থাকলে সেই ওয়েব ঠিকানা পাঠান (ইমেইল ঠিকানা পাতার নীচে আছে), অনুমোদিত এবং সম্পাদিত হলে লেখা এখানে প্রকাশিত হবে। ... আরও ...
- হরিদাস পালেরা
- এটি একটি খোলা পাতা, যাকে আমরা ব্লগ বলে থাকি। গুরুচন্ডালির সম্পাদকমন্ডলীর হস্তক্ষেপ ছাড়াই, স্বীকৃত ব্যবহারকারীরা এখানে নিজের লেখা লিখতে পারেন। সেটি গুরুচন্ডালি সাইটে দেখা যাবে। খুলে ফেলুন আপনার নিজের বাংলা ব্লগ, হয়ে উঠুন একমেবাদ্বিতীয়ম হরিদাস পাল, এ সুযোগ পাবেন না আর, দেখে যান নিজের চোখে...... আরও ...
- টইপত্তর
- নতুন কোনো বই পড়ছেন? সদ্য দেখা কোনো সিনেমা নিয়ে আলোচনার জায়গা খুঁজছেন? নতুন কোনো অ্যালবাম কানে লেগে আছে এখনও? সবাইকে জানান। এখনই। ভালো লাগলে হাত খুলে প্রশংসা করুন। খারাপ লাগলে চুটিয়ে গাল দিন। জ্ঞানের কথা বলার হলে গুরুগম্ভীর প্রবন্ধ ফাঁদুন। হাসুন কাঁদুন তক্কো করুন। স্রেফ এই কারণেই এই সাইটে আছে আমাদের বিভাগ টইপত্তর। ... আরও ...
- ভাটিয়া৯
- যে যা খুশি লিখবেন৷ লিখবেন এবং পোস্ট করবেন৷ তৎক্ষণাৎ তা উঠে যাবে এই পাতায়৷ এখানে এডিটিং এর রক্তচক্ষু নেই, সেন্সরশিপের ঝামেলা নেই৷ এখানে কোনো ভান নেই, সাজিয়ে গুছিয়ে লেখা তৈরি করার কোনো ঝকমারি নেই৷ সাজানো বাগান নয়, আসুন তৈরি করি ফুল ফল ও বুনো আগাছায় ভরে থাকা এক নিজস্ব চারণভূমি৷ আসুন, গড়ে তুলি এক আড়ালহীন কমিউনিটি ... আরও ...
- টইপত্তর, ভাটিয়া৯, হরিদাস পাল(ব্লগ) এবং খেরোর খাতার লেখার বক্তব্য লেখকের নিজস্ব, গুরুচণ্ডা৯র কোন দায়িত্ব নেই। | ♦ : পঠিত সংখ্যাটি ১৩ই জানুয়ারি ২০২০ থেকে, লেখাটি যদি তার আগে লেখা হয়ে থাকে তাহলে এই সংখ্যাটি সঠিক পরিমাপ নয়। এই বিভ্রান্তির জন্য আমরা দুঃখিত।












