- হরিদাস পাল আলোচনা বিবিধ

-
ইউক্লিড, মহলানবিশ, তথ্যবিজ্ঞান, অনলাইন বাজার ইত্যাদি
Angshuman Bhattacharya লেখকের গ্রাহক হোন
আলোচনা | বিবিধ | ১১ জুলাই ২০২০ | ৫৭৫৪ বার পঠিত [National Statistics day বা জাতীয় সংখ্যাতত্ত্ব দিবসে ভারতীয় সংখ্যাতত্ত্বের প্রাণপুরুষ প্রশান্তচন্দ্র মহলানবিশ জন্মদিনে সামান্য একজন তথ্য বিজ্ঞানীর শ্রদ্ধার্ঘ্য]
জ্যামিতির আদিপুরুষ ইউক্লিড অনেকগুলো প্রতিপাদ্য ও উপপাদ্য তৈরি করে গেছিলেন। যার একটি হল – কোন একটি জায়গায় যেকোনো দুটি বিন্দুর মধ্যে দূরত্ব নির্ণয়। মানে কোন একটি সমতলে দুটো বিন্দু একে অপরের থেকে কতটা দূরে আছে তা বের করার সহজ সুত্র। আবার কোন ত্রিমাত্রিক স্থানেও একই সূত্র দিয়ে আমরা দুটো বিন্দুর দূরত্ব বের করতে পারি। পরবর্তীতে এই ফর্মুলা আরো বিস্তার করে দেখানো হয় যে কোনো বহুমাত্রিক স্থানেও দুটি বিন্দুর দূরত্ব বের করা যায় ইউক্লিডের এই প্রতিপাদ্য দিয়ে। মানে ওই বহুমাত্রিক তলে কোন দুটি বিন্দুর প্রত্যেকটি মাত্রার মধ্যেকার দূরত্ব ব্যবহার করে ওই দুটি বিন্দুর মধ্যেকার আসল দূরত্ব বের করা যায়মানে যাকে বলে এন-ডাইমেনশন স্পেসে দুটো পয়েন্ট এর দূরত্ব নির্ণয়। ফর্মুলাটা অনেকটা এরকম (ছবি নং ১)।
সহজভাবে বলতে গেলে, যে কোন দুটি বিন্দুর দূরত্ব; তার প্রত্যেকটি মাত্রার অক্ষে ওই বিন্দু দুটি অবস্থানের দূরত্বের বর্গফলগুলো যোগ করলে যে রাশি পাওয়া যায়, তার বর্গমূল।
সাধারণ স্থানিক জ্যামিতি বা সরল ভৌগলিক দূরত্ব বা বহুমাত্রিক স্থানে দূরত্ব মাপার ক্ষেত্রে এই সুত্র সর্বজনীন ভাবে ব্যবহৃত হয়ে আসছে।
কিন্তু স্থানিক জ্যামিতির বাইরে এমন অনেক ব্যাপার আছে যেখানে দুটি বিন্দুর মধ্যে দূরত্ব বের করার দরকার পড়ে। সেটা কোন ফিজিক্যাল স্পেস বা সত্তিকারের স্থান নাও হতে পারে। সেটা হতে পারে কোন হাইপোথেটিক্যাল বা কল্পিত তল, যার মাত্রা গুলোর কিছু গাণিতিক মান আছে। যেমন একদল ছাত্রের অনেকগুলো বিষয়ে পরীক্ষায় প্রাপ্ত নম্বর। স্বাভাবিক ভাবেই একে অপরের থেকে বিভিন্ন বিষয়ে আলাদা নম্বর পেয়েছে। কিন্তু কোন দুজন ছাত্র বিভিন্ন বিষয়ের বিচারে কাছাকাছি আছে সেটা বের করব কি করে?
যদি একটা কল্পিত স্থান কল্পনা করে নিই, যার প্রত্যেকটা মাত্রা এক একটি বিষয়। এবার যদি প্রত্যেক বিষয়ে প্রাপ্ত নম্বর দিয়ে প্রত্যেকটি ছাত্রকে এক একটি বিন্দুতে নির্দিষ্ট করা হয়, তাহলে দেখা যাবে ছাত্ররা বিভিন্ন ভাবে ছড়িয়ে ছিটিয়ে থাকছে। কিছু ছাত্র কাছাকাছি থাকবে, কিছু আবার দূরে দূরে। ছাত্রদর একে অপরের থেকে দূরত্ব বের করা সম্ভব এই ইউক্লিডীয় সূত্র দিয়ে। অধিকাংশ ক্ষেত্রেই দেখা যাবে, বেশ কিছু ছাত্র খুব কাছাকাছি থেকে একটি দল তৈরি করেছে। আবার এরকম ছোট ছোট অনেকগুলো দল তৈরি হয়েছে; কোন দল বিজ্ঞান বিভাগে বেশি নম্বর পাওয়া ছাত্রদের দল, আবার কোন দল ভাষা ও সাহিত্যের বিভাগে বেশি নম্বর পাওয়া ছাত্র দল। আবার একদল দেখা যাবে সবক্ষেত্রেই সব বিষয় মোটামুটি নম্বর পেয়েছে, তারা অলরাউন্ডারের দল।
আবার ধরা যাক একটি অনলাইন বাজার আছে, তাতে অনেক ক্রেতা। সেই সংস্থার কাছে প্রত্যেক ক্রেতার নিজস্ব কিছু তথ্য আছে। যদি সেই তথ্যের ভিত্তিতে দুজন ক্রেতার মধ্যেকার দূরত্ব মাপতে চাই, তাহলে ইউক্লিডের এই ফর্মুলা কাজে লাগতে পারে। যেমন একটি অক্ষে রাখলাম ক্রেতাদের বয়স। আরেকটি অক্ষে ক্রেতাদের শিক্ষাগত যোগ্যতা। দুজন ক্রেতা দুটি বিন্দুতে অবস্থান করবেন এই কল্পিত স্থানে। এবং সহজেই তাদের মধ্যেকার দূরত্ব বা নৈকট্য আমরা মাপতে পারি। আবার আরেকটি অক্ষের কথা ভাবতে পারি যেখানে ক্রেতাদের বার্ষিক আয় প্লট করা হয়েছে। তাহলেও একটি ত্রিমাত্রিক স্থানে দূরত্ব নৈকট্য মাপতে পারবো।
কিন্তু এই মাপের মধ্যে একটা বড় গলদ রয়ে গেছে। তা হল এই অক্ষগুলো বা তুলনার মাপকাঠি গুলো পরস্পর সম্পৃক্ত। যেমন ক্রেতার বয়স বেশি হলে তার শিক্ষাগত যোগ্যতাও বেশি হবে। মানে একজন পনের বছরের বয়স্ক ক্রেতা কখনোই স্নাতকোত্তর হতে পারেন না। যদিও এটা একটা বয়সের পরে আর তেমন স্বতঃসিদ্ধও নয়। আবার শিক্ষাগত যোগ্যতার সাথে বার্ষিক আয়ের একটা সরাসরি যোগাযোগ আছে। এই পারস্পরিক সম্পৃক্ততার কারণে এই তথ্যগুলোর মধ্যে একটি বায়াস চলে আসবে। মানে অধিকাংশ উচ্চ আয়ের লোকেরা তাদের অধিক শিক্ষাগত যোগ্যতার কারণে খুব কাছাকাছি থাকবেন। ফলে আমাদের দূরত্ব নিরূপণ সঠিক হবে না এই ইউক্লিডীয় সূত্র দিয়ে, এবং নৈকট্যের একটি ভ্রান্ত পরিসংখ্যান পাব হয়তো।
প্রশান্তচন্দ্র মহলানবিশ সংখ্যাতত্ত্ববিদ হিসেবে এইখানে একটি অসামান্য অবদান রেখে গেছেন। উনি বুঝতে পেরেছিলেন যে যদি মাপকাঠি গুলো একে অপরের সঙ্গে সংযুক্ত থাকে, তাহলে ইউক্লিডীয় সূত্র দিয়ে দূরত্ব নিরূপণ অনেক সময় ব্যর্থ বা বিভ্রান্তিকর হতে পারে। তাই তিনি এই পদ্ধতির খানিকটা সংশোধন করে একটি নতুন রূপ দেন। উনি প্রস্তাব করলেন, যে মাপকাঠিগুলো পরস্পর সম্পৃক্ত, তাদেরকে আরও বেশি গুরুত্ব দেওয়া হোক। কিভাবে? মাপকাঠিগুলোর মধ্যেকার সম্পর্কের মান, যাকে সংখ্যাতত্ত্বের ভাষায় বলে কোরিলেশন, সেটা বের করে তারপর সেই দুটি বিষয়ের দূরত্বের বর্গকে কোরিলেশনের সমানুপাতিক গুন করা হোক। তারপর ইউক্লিডীয় সুত্রের বাকিটার প্রয়োগ। ফলে কি হলো যে বিষয়গুলো চরিত্রগতভাবে কাছাকাছি, তাদের দূরত্বের মান এক থাকলেও, এই ফর্মুলায় তার গুরুত্ব বেড়ে গেল। ফলে যে সমস্ত বিন্দুর নিজেদের কাছাকাছি থাকার কথা তারা স্বাভাবিক ভাবেই একে অপরের কাছে চলে আসল। আবার যারা স্রেফ সঙ্খ্যাতাত্বিক কারনে একে অপরের কাছে চলে এসেছিল, কিন্তু তেমন কোন চরিত্রগত সাদৃশ্য নেই, তারা যথাসম্ভব দূরে চলে গেল। এইভাবে, সঙ্খ্যাতাত্বিক যে বায়াস তৈরি হছিল, সেটা অনেকটাই দুরিভুত করা গেল।
আরো একটি গুরুত্বপূর্ণ বিষয় এই মহলানবীশ ফর্মুলায় সমাধান হয়। আমরা জানি যে বিভিন্ন মাত্রা বিভিন্ন এককে থাকতে পারে। যেমন আমাদের উদাহরণে একজন ক্রেতার বয়স দশ থেকে খুব বেশি হলে একশ হতে পারে। কিন্তু তাঁর বার্ষিক আয় হতে পারে ষাট হাজার টাকা থেকে ধরা যাক বারো লাখ টাকা। স্রেফ মান খুব বেশি হওয়ার জন্য বার্ষিক আয়ের দূরত্বের বর্গ অনেক বড় সংখ্যা হবে, এবং তা দূরত্বের মানকে সম্পূর্ণভাবে দখল করবে। বাকি সংখ্যাগুলো খুব ছোট হওয়ার জন্য তেমন কোনো কাজে আসবে না। মহলানবীশ প্রস্তাব রাখলেন যে প্রত্যেকটি মাপকাঠি কে একই মাত্রায় নিয়ে আসতে হবে। সেটা কি করে সম্ভব? যদি আমরা প্রত্যেকটি মাপকাঠি কে শূন্য থেকে এক এই মাত্রায় নিয়ে আসি, যাকে সংখ্যাতাত্ত্বিক ভাষায় বলে স্ট্যান্ডার্ডাইজেশন, তাহলে এই ছোট বড় এককের ঝামেলা থেকে মুক্তি পাবো। (ছবি নং ২)
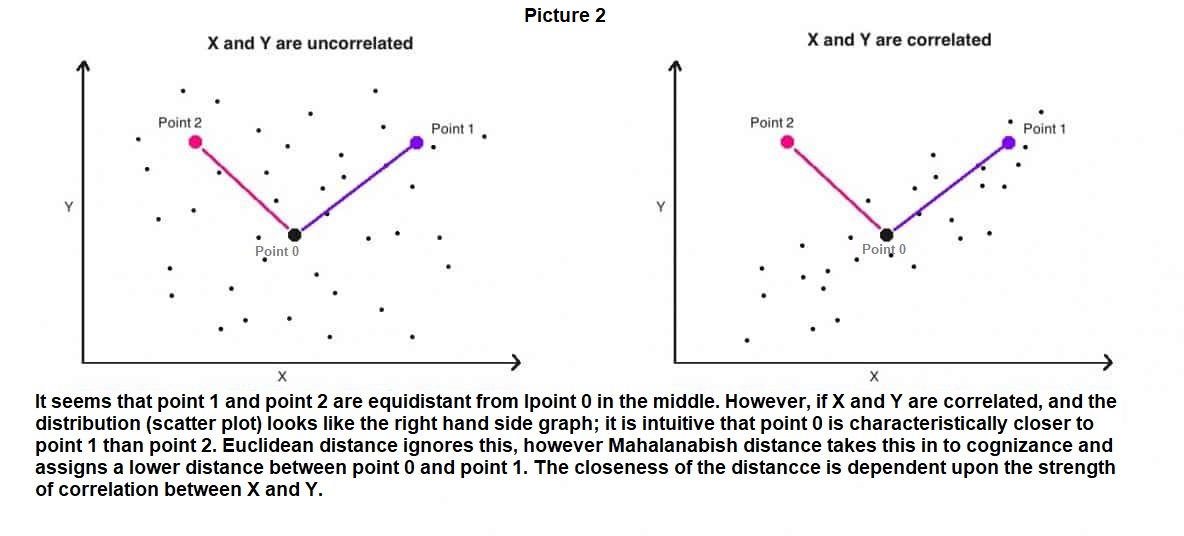
ইউক্লিড তার সূত্র নির্ধারণ করেছিলেন জ্যামিতির পরিপ্রেক্ষিতে যেখানে প্রত্যেকটি অক্ষই সমান এককে আছে। কিন্তু সংখ্যাতত্ত্বের চত্বরে যেখানে মহলানবিশ এর কাজ সেখানে এই সমান একক পাওয়া দুষ্কর। বরঞ্চ এককের বিভিন্নতাই সেখানে দস্তুর। তাই এই ছোট্ট কিন্তু অসীম সম্ভাবনাময় সমাধান, এককের একমাত্রিকরণ পদ্ধতি, এই সমস্যা থেকে প্রায় সম্পূর্ণভাবে মুক্তি দিতে পেরেছে।
এইভাবে মহলানবীশ একটি বিভিন্নধর্মী বহুমাত্রিক ব্যাবস্থায়, যেখানে আবার মাপকাঠি গুলোর পারস্পরিক সম্পর্ক গুরুত্বপূর্ণ, সেইখানে দুটি বিন্দুর দূরত্ব পরিমাপ করার সহজ ও সর্বজনগ্রাহ্য পদ্ধতি সুত্র তৈরি করলেন। আধুনিক সংখ্যাতত্ত্বে অত্যন্ত জরুরী এই অবদান। এর সংখ্যাতাত্ত্বিক নাম মহলানবিশ ডিসটেন্স বা মহলানবিশ দূরত্ব; ইউক্লিডীয় দূরত্বের সঙ্গে সঙ্গতি রেখে। ১৯৩৬ সালে প্রশান্তচন্দ্র মহলানবিশ এই ফর্মুলা তৈরি করেন।
কিন্তু আমাদের ব্যবহারিক জীবনে এর তাৎপর্য কি? শুরু করেছিলাম অনলাইন বাজারের গল্প দিয়ে। শুধু অনলাইন কেন, যেকোনো বাজার বা বড় দোকানের একটি প্রধান উদ্দেশ্য তার ক্রেতাকে ভালোভাবে চেনা। যত ভালোভাবে একটি অনলাইন বাজার তার ক্রেতাকে বুঝতে পারবেন, তাঁর ডেমোগ্রাফিক পরিচয়, তাঁর পছন্দ অপছন্দ, তাঁর খরচ করবার ইচ্ছে, ক্রয়ক্ষমতা ইত্যাদি যত ভালোভাবে বুঝতে পারবেন, তাকে সেই অনুযায়ী পণ্য সুপারিশ করতে পারবেন, সেই অনুযায়ী তাঁর চাহিদাকে খানিকটা প্রভাবিত করতে পারবেন। যদি সমস্ত ক্রেতাকে বিভিন্ন মাপকাঠি অনুযায়ী তাদের দূরত্ব বা নৈকট্যের প্রেক্ষিতে সাজাতে পারি, তাহলে সহজেই কিছু কিছু ক্রেতাকে আমরা একটা দলে রাখতে পারি, যারা একে অপরের খুব কাছের। এভাবে অনেকগুলো দল তৈরি যায়, যারা বেশ কিছু বিষয়ে একে অপরের খুব কাছাকাছি। বিভিন্ন দল বিভিন্ন বিষয়ে কাছাকাছি হবেন।
বাণিজ্যিক পরিভাষায় একেই বলে কাস্টমার সেগমেন্টেশন। আর যে পদ্ধতিতে এই সেগমেন্টেশন তৈরি করা হয়, সংখ্যাতাত্ত্বিক ভাষায় তাকে বলে ক্লাস্টারিং। এই ক্লাস্টার তৈরি করতে গেলে প্রথমেই সমস্ত ক্রেতাদের মধ্যেকার দূরত্ব বহুমাত্রিক ব্যাবস্থায়, মানে সবগুলো মাপকাঠির হিসেবে দূরত্ব তৈরি করতে হয়। যে দূরত্ব তৈরি করা যায় সবচেয়ে ভালোভাবে সেটা এই মহলানবীশ ডিসটেন্স ফর্মুলা দিয়ে। তারপর যে যে ক্রেতাদের মধ্যে দূরত্ব সবচেয়ে কম তাদেরকে একটি গ্রুপে বা দলে রাখা যায়।

এই একই দলের ক্রেতারা যেহেতু বিভিন্ন মাপকাঠিতে প্রায় একই রকম, এটা বোধহয় তাই ধারণা করা যায় যে এই দল সাধারণভাবে একই ধরনের পণ্যে আকৃষ্ট হবেন। ফলে যদি দেখা যায় একটি দলের অনেক সদস্য একটি নির্দিষ্ট ব্র্যান্ডের জিন্স কিনেছেন তাহলে ওই দলের মধ্যেই যিনি এখনো জিন্স কেনেননি তাকে সেই ব্র্যান্ডটা সুপারিশ করা যেতেই পারে।
এভাবেই আমাদের কাছে নিত্যনতুন পণ্যের বিজ্ঞাপন আসে। অনলাইন বাজার গুলো প্রথমে পর্যালোচনা করে আমি কোন দলে পড়ি, আমার সমস্ত মাপকাঠি খতিয়ে দেখে। তারপর সেই দলের অন্যান্য সদস্যরা যা যা কিনেছেন সেগুলো আমার ক্ষেত্রেও প্রযোজ্য হবে এইরকম একটি ধারণা করা হয়। তারপর সেই পন্যের বিজ্ঞাপন আমার কাছে আসে। এই ধারণা যে ভুল নয় আমরা আজ খুব ভালোভাবে বুঝে গেছি, কারণ সে বিজ্ঞাপনগুলো সত্যিই আমাদের আকর্ষণ করে। এবং আমরা অনেক কিছুই এইভাবে কিনে থাকি।
ঠিক একইভাবে নেটফ্লিক্স বা আমাজন প্রাইম এর হিসেবে আপনি যে দলে পড়েন পড়েন, সেই দলের অন্যান্য সদস্যরা ছবি যে যে দেখেন, আপনার না দেখা হয়ে থাকলে সেই ছবি আপনাকে সুপারিশ করা হচ্ছে এবং আপনি পরের সুযোগেই সেই ছবিটি দেখে ফেলছেন। এই সমস্ত কার্যকলাপ হয়ে চলেছে যে পদ্ধতিতে তার পেছনে আছে অনেকগুলো মেশিন লার্নিং অ্যালগরিদম। তার প্রথমটাই হচ্ছে কাস্টমার সেগমেন্টেশন বা ক্লাস্টারিং করা, যার ভিত হচ্ছে ক্রেতাদের মধ্যেকার দূরত্ব নির্ণয় নৈকট্যের পরিমাপ; যা সম্ভব হয়ে উঠছে মহলানবিশ ডিসটেন্সের মাধ্যমে।
আবার যখন একজন নতুন ক্রেতা বা দর্শক এই অনলাইন বাজারের নাম লেখা দেখান তখন প্রথমেই তাকে একটি দলে ফেলে দেওয়া হয় তার ডেমোগ্রাফিক ও অন্যান্য মাপকাঠির হিসেবে। যাতে করে শুরুর দিন থেকেই তাকে নিত্য-নতুন পণ্য বা অনুষ্ঠানের সুপারিশ দেয়া যেতে পারে। এই দলে ফেলে দেওয়ার কাজটি করে ক্লাস্টারিং অ্যালগরিদম, যার মূল কথা দূরত্ব বা নৈকট্য নিরূপণ, যার গোড়ায় আছে যার মহলানবিশ ডিসটেন্স।
29 শে জুন দিনটি ভারতবর্ষে পালিত হয় জাতীয় সংখ্যাতত্ত্ব দিবস বা নেশনাল স্টাটিস্টিকস ডে হিসেবে, প্রশান্তচন্দ্র মহলানবিশের জন্মদিন মনে রেখে। তাঁর অনেক কীর্তি আছে - ইন্ডিয়ান স্ট্যাটিস্টিক্যাল ইনস্টিটিউট স্থাপন, প্রথম পঞ্চবার্ষিকী পরিকল্পনা তৈরি করা এবং ভবিষ্যতের পঞ্চবার্ষিকী পরিকল্পনা গুলোর একটি সংখ্যাতাত্ত্বিক ভিত তৈরি করে দেওয়া। এগুলো বহুচর্চিত। তবে আধুনিক তথ্যবিজ্ঞানে তাঁর আবিষ্কৃত ফর্মুলা কিভাবে কাজে লাগছে, কিভাবে মেশিন লার্নিংয়ের একটি জরুরি ভিত্তিপ্রস্তর আসলে এই বাঙালী বিজ্ঞানীর অবদান, যা আমাদের দৈনন্দিন অনলাইন জীবনকে নিয়ত প্রভাবিত করছে, এই দিকটি তুলে ধরার জন্যই এই প্রবন্ধ।
পুনঃপ্রকাশ সম্পর্কিত নীতিঃ এই লেখাটি ছাপা, ডিজিটাল, দৃশ্য, শ্রাব্য, বা অন্য যেকোনো মাধ্যমে আংশিক বা সম্পূর্ণ ভাবে প্রতিলিপিকরণ বা অন্যত্র প্রকাশের জন্য গুরুচণ্ডা৯র অনুমতি বাধ্যতামূলক। লেখক চাইলে অন্যত্র প্রকাশ করতে পারেন, সেক্ষেত্রে গুরুচণ্ডা৯র উল্লেখ প্রত্যাশিত।- আরও পড়ুনফলিবেই ফলিবে (২০২৬) - যদুবাবুআরও পড়ুনকাজির বিচার - প্রবুদ্ধ বাগচীআরও পড়ুনবেঙ্গল এডুকেশন অব টেকনোলজি অ্যান্ড ম্যানেজমেন্ট[B.I.T.M] : শিক্ষা ব্যবস্থার কলঙ্ক - albert banerjeeআরও পড়ুনঘ - শর্মিষ্ঠা
- মতামত দিন
-
বিষয়বস্তু*:
-
Sudipto Pal | ১২ জুলাই ২০২০ ১২:৫৬95156
- খুব ভালো লেখা | তবে সম্পৃক্ত না বলে সম্পর্কিত বললে ভালো হত | সম্পৃক্ত মানে স্যাচুরেটেড | বাংলায় পরিসংখ্যানবিদ্যা নিয়ে এমন লেখা আরও আসা উচিত
 স্বাতী রায় | 2402:3a80:a87:5486:56cb:4a86:e861:***:*** | ১২ জুলাই ২০২০ ১৬:৪০95165
স্বাতী রায় | 2402:3a80:a87:5486:56cb:4a86:e861:***:*** | ১২ জুলাই ২০২০ ১৬:৪০95165- বা: খুব ভাল লাগল। প্রশান্ত চন্দ্র মহলানবিশের এই কাজগুলোর কথা জানা ছিল না। জানানোর জন্য ধন্যবাদ।
-
Angshuman Bhattacharya | ১৩ জুলাই ২০২০ ১৩:১৮95173
@Sudipto ধন্যবাদ । আপনি ঠিক বলেছেন। সম্পর্কিত হওয়া উচিত। বা সম্পর্কযুক্ত। এডিট করে দিচ্ছি।
ডেটা সায়েন্স , যাকে আমি বলি তথ্য বিজ্ঞান, তার উপর লেখার চেষ্টা করছি। আমাদের দৈনন্দিন জীবনে এর ব্যবহার এবং প্রভাব কোথায়, সেই সব। এর সাথে চেষ্টা করি বিখ্যাত পরিসংখ্যানবিদ / গণিতবিদ / বিজ্ঞানীদের অবদান তুলে ধরতে। যেখানে সম্ভব । এর সাথে ভারতীয় বিজ্ঞানীদের বিশেষ রেফারেন্স সহ, যেখানে খুঁজে পাই।
@Swati, ধন্যবাদ । পিসিএম এর বিভিন্ন ক্ষেত্রের উপর অনেক কাজ রয়েছে । আমার জ্ঞান সীমিত, কিন্তু আমাকে তাঁর ভক্ত বলতে পারেন। তাঁর কাজের উপর আরো লেখার চেষ্টা করবো।
 ar | 96.23.***.*** | ১৩ জুলাই ২০২০ ১৮:৪৬95175
ar | 96.23.***.*** | ১৩ জুলাই ২০২০ ১৮:৪৬95175- @Angshuman Bhattacharya
খুব ভাল লাগল।
সাংখ্য (জার্নাল) নিয়ে যদি কিছু লেখেন তো খুব ভাল হয়। প্রশান্তচন্দ্র মহালনবিশের এই অবদানের কথা সবাই ভুলতে বসেছে।
 অরুণাভ | 202.8.***.*** | ১৪ জুলাই ২০২০ ০০:৩৫95181
অরুণাভ | 202.8.***.*** | ১৪ জুলাই ২০২০ ০০:৩৫95181- খুব ভালো লাগলো লেখাটা।
 রঞ্জন | 182.64.***.*** | ১৪ জুলাই ২০২০ ১৯:১৯95211
রঞ্জন | 182.64.***.*** | ১৪ জুলাই ২০২০ ১৯:১৯95211@Angshuman Bhattacharya
ভাবছি আগে কী করে মিস করে গেছলাম। খুব ভালো বুঝিয়েছেন। আরও লেখা চাই । জি বি এস হ্যালডেনকে নিয়ে কিছু লিখবেন?
 Rezwanul Haque. | 203.96.***.*** | ১৪ জুলাই ২০২০ ২৩:০৭95219
Rezwanul Haque. | 203.96.***.*** | ১৪ জুলাই ২০২০ ২৩:০৭95219"The Indonesian constitution declared in Chapter XI that
(1) The State shall be based upon the belief in the One and Only God."
-Never undermine the strength of Islam and our sacred tenet of TAWHID in the Holy Quran, TAWHID signifying oneness of God. Yes, Indonesia is not as strictly religious as Afghanistan, Maldives, Pakistan or Bangladesh, but gradually it will be an Islamic state too. Martyrdom of souls like Imam Samudra in Bali bomb blast will not go futuile...INSHALLAH!
-
শিবাংশু | ১৫ জুলাই ২০২০ ২১:৩১95249
- বিষয়টি আপাত ভাবে সরল নয়। কিন্তু সহজভাবে লেখা হয়েছে। চার দশকের উপর হয়ে গেলো, স্টেট ব্যাংকে মার্কেট সেগমেন্টেশনের উপর ভিত্তি করে গণব্যাংকিংয়ের যে মডেল তৈরি করা হয়েছিলো, তার উৎস রয়েছে এই তত্ত্বটিতে। এই তত্ত্বটির বৈপ্লবিক সম্ভাবনা সে সময় অন্যান্য ব্যাংক ও আর্থিক সংস্থাগুলি বুঝতে অনেক দেরি করেছিলো।
লেখককে অনেক ধন্যবাদ।
 কুশান | 103.87.***.*** | ১৫ জুলাই ২০২০ ২২:১৫95250
কুশান | 103.87.***.*** | ১৫ জুলাই ২০২০ ২২:১৫95250- খুব ভালো লাগলো। এই কোরিলেশন এর জায়গা এবং তার উদাহরণ এবং মানগত অসুবিধের জায়গাটা ও তার (0,1) এর প্রস্তাবনা খুব সুন্দর ব্যাখ্যা করেছেন।
ফ্র্যাক্টাল নিয়ে পারলে এইরকম কিছু লিখুন না।
 চিরঞ্জীবনিয়োগী | 103.27.***.*** | ২২ জুলাই ২০২০ ২১:৩৩95427
চিরঞ্জীবনিয়োগী | 103.27.***.*** | ২২ জুলাই ২০২০ ২১:৩৩95427লেখাটি বেশ ভালোলাগলো । দৈনন্দিন জীবনে সংখ্যাতত্ত্বের ব্যবহারিক প্রয়োগের উদাহরণগুলো বেশ চিত্তাকর্ষ। এতখানি তলিয়ে আমরা অনেকেই ভেবে দেখি না। আপনার আরও কিছু লেখা প্রকাশের অপেক্ষায় রইলাম৷
 প্রত্যয় | 2600:100b:b019:7c4b:1828:5359:1628:***:*** | ২৩ জুলাই ২০২০ ০৭:৪৭95437
প্রত্যয় | 2600:100b:b019:7c4b:1828:5359:1628:***:*** | ২৩ জুলাই ২০২০ ০৭:৪৭95437সাধু প্রচেষ্টা। তবে এই জায়গাটায় গোলমাল আছে -
"উনি প্রস্তাব করলেন, যে মাপকাঠিগুলো পরস্পর সম্পৃক্ত, তাদেরকে আরও বেশি গুরুত্ব দেওয়া হোক। কিভাবে? মাপকাঠিগুলোর মধ্যেকার সম্পর্কের মান, যাকে সংখ্যাতত্ত্বের ভাষায় বলে কোরিলেশন, সেটা বের করে তারপর সেই দুটি বিষয়ের দূরত্বের বর্গকে কোরিলেশনের সমানুপাতিক গুন করা হোক। তারপর ইউক্লিডীয় সুত্রের বাকিটার প্রয়োগ।"
কোরিলেশন বার করা হচ্ছে মাপকাঠি, অর্থাৎ ভেরিয়েবল গুলোর মধ্যে। আর দূরত্ব মাপার সময় একেকটা ভেরিয়েবল ধরে ধরে তাদের মধ্যে দূরত্ব মাপা হচ্ছে। দুটো ভেরিয়েবলের মধ্যের দূরত্বের কথার অর্থ কি?
ওনার প্রস্তাব অনুযায়ী যে মাপকাঠি/ভেরিয়েবল গুলো কোরিলেটেড তাদের বেশি গুরুত্ব দেওয়া হোক এই কথাও ঠিক নয়।
এছাড়া প্রচুর টাইপো/বানান ভুল আছে, যা মোটের ওপর অগ্রাহ্য করলেও যাঁকে শ্রদ্ধার্ঘ্য, তাঁর নামের বানান বারবার নানান রকমের ভুল করাটা চোখে লাগে। আরও যত্ন নিয়ে লেখা যেত।
 অংশু | 2401:4900:1044:d8a3:ddde:b341:a455:***:*** | ০১ আগস্ট ২০২০ ১৩:৩৩95798
অংশু | 2401:4900:1044:d8a3:ddde:b341:a455:***:*** | ০১ আগস্ট ২০২০ ১৩:৩৩95798@ar সাংখ্য নিয়ে লিখতে চাই, কিন্তু অনেকটা গবেষণা বাকি আছে। চেষ্টা করব তাড়াতাড়ি লেখার।
 অংশু | 2401:4900:1044:d8a3:ddde:b341:a455:***:*** | ০১ আগস্ট ২০২০ ১৩:৩৯95799
অংশু | 2401:4900:1044:d8a3:ddde:b341:a455:***:*** | ০১ আগস্ট ২০২০ ১৩:৩৯95799@রঞ্জন ধন্যবাদ। জে বি এস হ্যালডেন আমার খুবই শ্রদ্ধার বিজ্ঞানী। কলকাতাবাসী হিসেবে আমরা ধন্য যে উনি এই শহরটাকে বেছে নিয়েছিলেন ওনার কর্মক্ষেত্র হিসেবে । তবে আমার সামর্থ্য সীমিত। তথ্য বিজ্ঞান মেশিন লার্নিং সংখ্যাতত্ত্ব এইসব বিষয়ে থাকার চেষ্টা করি। তবুও লেখার চেষ্টা করব।
 অংশু | 2401:4900:1044:d8a3:ddde:b341:a455:***:*** | ০১ আগস্ট ২০২০ ১৩:৪২95800
অংশু | 2401:4900:1044:d8a3:ddde:b341:a455:***:*** | ০১ আগস্ট ২০২০ ১৩:৪২95800@ শিবাংশু অনেক ধন্যবাদ। মার্কেট সেগমেনটেশন এ ক্লাস্টারিং অ্যালগরিদম খানিকটা ব্যাবহার হয়। স্টেট ব্যাঙ্ক অনেক ব্যাপারেই পথিকৃৎ। তবে ইদানিং প্রাইভেট ব্যাঙ্কগুলি এই সব ব্যাপারে অনেক এগিয়ে গেছে।
- মতামত দিন
-
বিষয়বস্তু*:
-
গুরুচণ্ডা৯-র বই দত্তক নিন
কোনোরকম কর্পোরেট ফান্ডিং ছাড়া সম্পূর্ণরূপে জনতার শ্রম ও অর্থে পরিচালিত এই নন-প্রফিট এবং স্বাধীন উদ্যোগটিকে বাঁচিয়ে রাখতে এককালীন বা ধারাবাহিক ভাবে গুরুভার বহন করুন।
- ভাটিয়ালি | টইপত্তর | বুলবুলভাজা | হরিদাস পাল | খেরোর খাতা | বই
- বুলবুলভাজা : সর্বশেষ লেখাগুলি
(লিখছেন... দ)
(লিখছেন... Juin, Dr. Barnali Ray Basu, Bratin Das)
(লিখছেন... Biswajit Roy, কল্যাণ, Somenath Guha)
(লিখছেন... )
(লিখছেন... শিবাংশু)
- হরিদাস পালেরা : যাঁরা সম্প্রতি লিখেছেন
(লিখছেন... Manali Moulik, dc, শ্রীমল্লার বলছি)
(লিখছেন... দীপ)
(লিখছেন... )
(লিখছেন... aranya, bikarna, bikarna)
(লিখছেন... Amit, সুকি , বিপ্লব রহমান)
- টইপত্তর : সর্বশেষ লেখাগুলি
(লিখছেন... albert banerjee, বোদাগু, albert banerjee)
(লিখছেন... )
(লিখছেন... বোদাগু, albert banerjee)
(লিখছেন... )
(লিখছেন... )
- কি, কেন, ইত্যাদি
- বাজার অর্থনীতির ধরাবাঁধা খাদ্য-খাদক সম্পর্কের বাইরে বেরিয়ে এসে এমন এক আস্তানা বানাব আমরা, যেখানে ক্রমশ: মুছে যাবে লেখক ও পাঠকের বিস্তীর্ণ ব্যবধান। পাঠকই লেখক হবে, মিডিয়ার জগতে থাকবেনা কোন ব্যকরণশিক্ষক, ক্লাসরুমে থাকবেনা মিডিয়ার মাস্টারমশাইয়ের জন্য কোন বিশেষ প্ল্যাটফর্ম। এসব আদৌ হবে কিনা, গুরুচণ্ডালি টিকবে কিনা, সে পরের কথা, কিন্তু দু পা ফেলে দেখতে দোষ কী? ... আরও ...
- আমাদের কথা
- আপনি কি কম্পিউটার স্যাভি? সারাদিন মেশিনের সামনে বসে থেকে আপনার ঘাড়ে পিঠে কি স্পন্ডেলাইটিস আর চোখে পুরু অ্যান্টিগ্লেয়ার হাইপাওয়ার চশমা? এন্টার মেরে মেরে ডান হাতের কড়ি আঙুলে কি কড়া পড়ে গেছে? আপনি কি অন্তর্জালের গোলকধাঁধায় পথ হারাইয়াছেন? সাইট থেকে সাইটান্তরে বাঁদরলাফ দিয়ে দিয়ে আপনি কি ক্লান্ত? বিরাট অঙ্কের টেলিফোন বিল কি জীবন থেকে সব সুখ কেড়ে নিচ্ছে? আপনার দুশ্চিন্তার দিন শেষ হল। ... আরও ...
- বুলবুলভাজা
- এ হল ক্ষমতাহীনের মিডিয়া। গাঁয়ে মানেনা আপনি মোড়ল যখন নিজের ঢাক নিজে পেটায়, তখন তাকেই বলে হরিদাস পালের বুলবুলভাজা। পড়তে থাকুন রোজরোজ। দু-পয়সা দিতে পারেন আপনিও, কারণ ক্ষমতাহীন মানেই অক্ষম নয়। বুলবুলভাজায় বাছাই করা সম্পাদিত লেখা প্রকাশিত হয়। এখানে লেখা দিতে হলে লেখাটি ইমেইল করুন, বা, গুরুচন্ডা৯ ব্লগ (হরিদাস পাল) বা অন্য কোথাও লেখা থাকলে সেই ওয়েব ঠিকানা পাঠান (ইমেইল ঠিকানা পাতার নীচে আছে), অনুমোদিত এবং সম্পাদিত হলে লেখা এখানে প্রকাশিত হবে। ... আরও ...
- হরিদাস পালেরা
- এটি একটি খোলা পাতা, যাকে আমরা ব্লগ বলে থাকি। গুরুচন্ডালির সম্পাদকমন্ডলীর হস্তক্ষেপ ছাড়াই, স্বীকৃত ব্যবহারকারীরা এখানে নিজের লেখা লিখতে পারেন। সেটি গুরুচন্ডালি সাইটে দেখা যাবে। খুলে ফেলুন আপনার নিজের বাংলা ব্লগ, হয়ে উঠুন একমেবাদ্বিতীয়ম হরিদাস পাল, এ সুযোগ পাবেন না আর, দেখে যান নিজের চোখে...... আরও ...
- টইপত্তর
- নতুন কোনো বই পড়ছেন? সদ্য দেখা কোনো সিনেমা নিয়ে আলোচনার জায়গা খুঁজছেন? নতুন কোনো অ্যালবাম কানে লেগে আছে এখনও? সবাইকে জানান। এখনই। ভালো লাগলে হাত খুলে প্রশংসা করুন। খারাপ লাগলে চুটিয়ে গাল দিন। জ্ঞানের কথা বলার হলে গুরুগম্ভীর প্রবন্ধ ফাঁদুন। হাসুন কাঁদুন তক্কো করুন। স্রেফ এই কারণেই এই সাইটে আছে আমাদের বিভাগ টইপত্তর। ... আরও ...
- ভাটিয়া৯
- যে যা খুশি লিখবেন৷ লিখবেন এবং পোস্ট করবেন৷ তৎক্ষণাৎ তা উঠে যাবে এই পাতায়৷ এখানে এডিটিং এর রক্তচক্ষু নেই, সেন্সরশিপের ঝামেলা নেই৷ এখানে কোনো ভান নেই, সাজিয়ে গুছিয়ে লেখা তৈরি করার কোনো ঝকমারি নেই৷ সাজানো বাগান নয়, আসুন তৈরি করি ফুল ফল ও বুনো আগাছায় ভরে থাকা এক নিজস্ব চারণভূমি৷ আসুন, গড়ে তুলি এক আড়ালহীন কমিউনিটি ... আরও ...
- টইপত্তর, ভাটিয়া৯, হরিদাস পাল(ব্লগ) এবং খেরোর খাতার লেখার বক্তব্য লেখকের নিজস্ব, গুরুচণ্ডা৯র কোন দায়িত্ব নেই। | ♦ : পঠিত সংখ্যাটি ১৩ই জানুয়ারি ২০২০ থেকে, লেখাটি যদি তার আগে লেখা হয়ে থাকে তাহলে এই সংখ্যাটি সঠিক পরিমাপ নয়। এই বিভ্রান্তির জন্য আমরা দুঃখিত।















